
5.1退化模型 若G(u,v),F(u,v)和N(,v)分别是g(m,n),f(m,n和 7(m,n)的二维傅立叶变换,则有 G(u,v)=H(u,v)F(u,v)+N(u,v) (5.1.27) w=0,1,…,M-1v=0,1,…,N-1 这样整个的求解过程就得到了简化。如果系统是线性移 不变的,在空间域中建立的退化模型可通过分块循环矩阵对 角化导出频域中的恢复滤波器,将庞大的空域运算转化为相 对较少的频域运算。上式对应我们即将讨论的频域退化模 型。 Digital Image Processing
Digital Image Processing Digital Image Processing 若 , 和 分别是 , 和 的二维傅立叶变换,则有 的二维傅立叶变换,则有 (5.1.27) 这样整个的求解过程就得到了简化。如果系统是线性移 这样整个的求解过程就得到了简化。如果系统是线性移 不变的,在空间域中建立的退化模型可通过分块循环矩阵对 不变的,在空间域中建立的退化模型可通过分块循环矩阵对 角化导出频域中的恢复滤波器,将庞大的空域运算转化为相 角化导出频域中的恢复滤波器,将庞大的空域运算转化为相 对较少的频域运算。上式对应我们即将讨论的频域退化模 对较少的频域运算。上式对应我们即将讨论的频域退化模 型。 (,) (,) (,) (,) 0,1, , 1; 0,1, , 1 Guv HuvFuv Nuv u Mv N = + = " " −= − Guv (,) Fuv (,) Nuv (,) (,) 5.1 退化模型 g m n f (,) m n η(,) m n
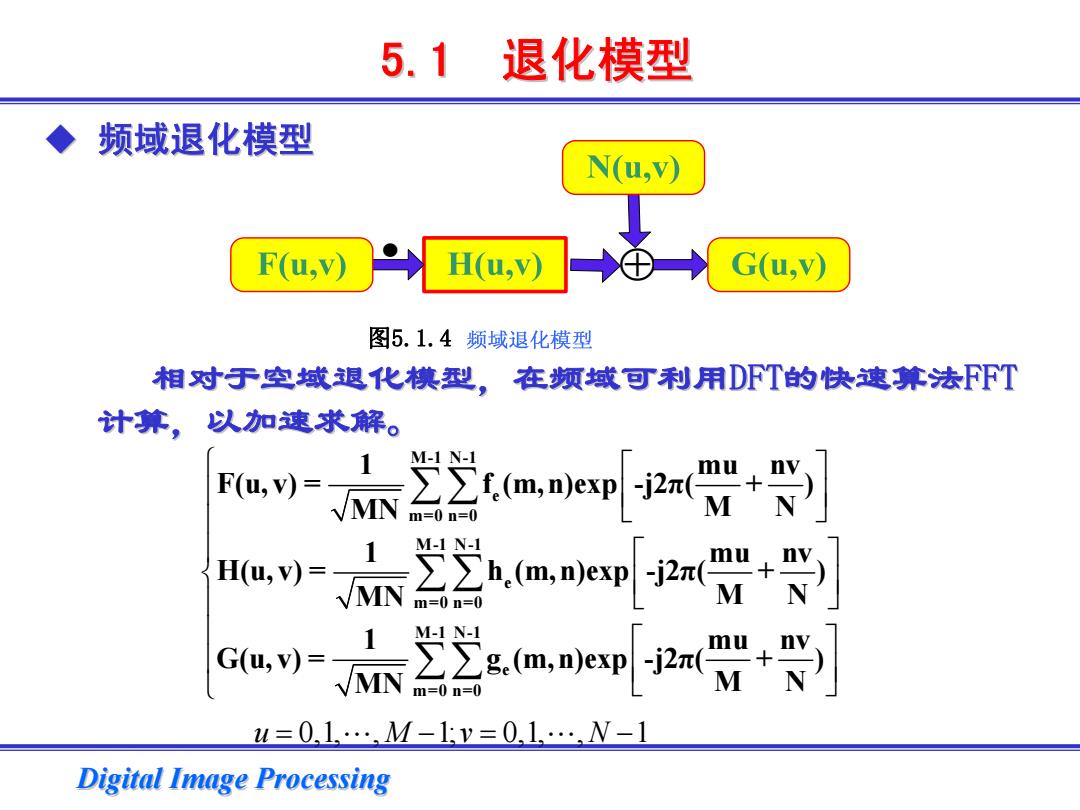
5.1退化模型 频域退化模型 N(u,v) F(u,v) H(u,v) G(u,v) 图5.1.4频域退化模型 相对于空域退化模型,在频域可利用DFT的快速算法FFT 计算,以加速求解。 1 M-1N-1 F(u,v)= MN 空mep+贷 m=0n=0 N H(u,v)= 1 M-1N-1 nv MN h.(m.m)esp m=0n=0 N G(u,)= 不22aep+ M-1N-1 m=0n=0 u=0.1…M-1:y=0.1…,W-1 Digital Image Processing
Digital Image Processing Digital Image Processing 频域退化模型 相对于空域退化模型,在频域可利用 相对于空域退化模型,在频域可利用DFT的快速算法FFT 计算,以加速求解。 计算,以加速求解。 5.1 退化模型 ⎧ ⎡ ⎤ ⎪ ⎢ ⎥ ⎣ ⎦ ⎪⎪ ⎡ ⎤ ⎨ ⎢ ⎥ ⎪ ⎣ ⎦ ⎪ ⎡ ⎤ ⎪ ⎢ ⎥ ⎩ ⎣ ⎦ ∑∑∑∑∑∑ M-1 N-1 e m=0 n=0 M-1 N-1 e m=0 n=0 M-1 N-1 e m=0 n=0 1 mu nv F(u, v) = f (m,n)exp -j2π( +) MN M N 1 mu nv H(u, v) = h (m,n)exp -j2π( +) MN M N 1 mu nv G(u, v) = g (m,n)exp -j2π( +) MN M N u Mv N = −= − 0,1, , 1; 0,1, , 1 " " ⊕ • 图5.1.4

5.2常见退化函数及其辨识方法 ◆退化函数h(m,n)的先验知识: (1)h(m,n)是确定性并且非负的。 (2)h(m,n)具有有限支持域。 (3)退化过程并不损失图像的能量,即 ∑∑h(m,叫=1。 Digital Image Processing
Digital Image Processing Digital Image Processing 退化函数h(m,n)的先验知识: (1) h(m,n)是确定性并且非负的。 是确定性并且非负的。 (2) h(m,n)具有有限支持域。 具有有限支持域。 (3) 退化过程并不损失图像的能量 退化过程并不损失图像的能量,即 。 5.2 常见退化函数及其辨识方法 常见退化函数及其辨识方法 ∑∑ m n h(m,n) = 1

5.2常见退化函数及其辨识方法 ◆几种常见的退化模型 1.线性运动退化函数 线性运动退化是由于目标与成像系统间的相对勻速直线运动形成的 退化。水平方向的线性运动可以用以下退化函数来表示 0≤m≤d且n=0 else 其中表示退化函数的长度。对于线性移动为其它方向的情况,也 可以用类似的方法进行定义。 Digital Image Processing
Digital Image Processing Digital Image Processing 几种常见的退化模型 几种常见的退化模型 1. 线性运动退化函数 线性运动退化函数 线性运动退化是由于目标与成像系统间的相对匀速直线运动形成的 退化。水平方向的线性运动可以用以下退化函数来表示 其中d表示退化函数的长度。对于线性移动为其它方向的情况,也 可以用类似的方法进行定义。 5.2 常见退化函数及其辨识方法 常见退化函数及其辨识方法 1 ;0 0 (,) 0 ; d md n hmn else ⎧ ≤ ≤ = = ⎨⎩ 且

5.2常见退化函数及其辨识方法 2.散退化函数 几何光学的分析表明,光学系统散廉造成的图像退化对应的点扩散函数 应该是一个均匀分布的圆形光班,如图5.2.1(f)所能看到的。该退化函数 可以表示为 1/(πR2);2+v2≤R2 H(u,v)= 0 else 其中R是牧廉斑的半径。在信噪比校高的情况下,在频域图上可以观察 到圆形的轨迹。 Digital Image Processing
Digital Image Processing Digital Image Processing 2.散焦退化函数 几何光学的分析表明,光学系统散焦造成的图像退化对应的点扩散函数 应该是一个均匀分布的圆形光斑,如图5.2.1(f)所能看到的。该退化函数 可以表示为 其中R是散焦斑的半径。在信噪比较高的情况下,在频域图上可以观察 到圆形的轨迹。 5.2 常见退化函数及其辨识方法 常见退化函数及其辨识方法 2 22 2 1/( ) ; (,) 0 ; R uvR Huv else ⎧ π + ≤ = ⎨⎩