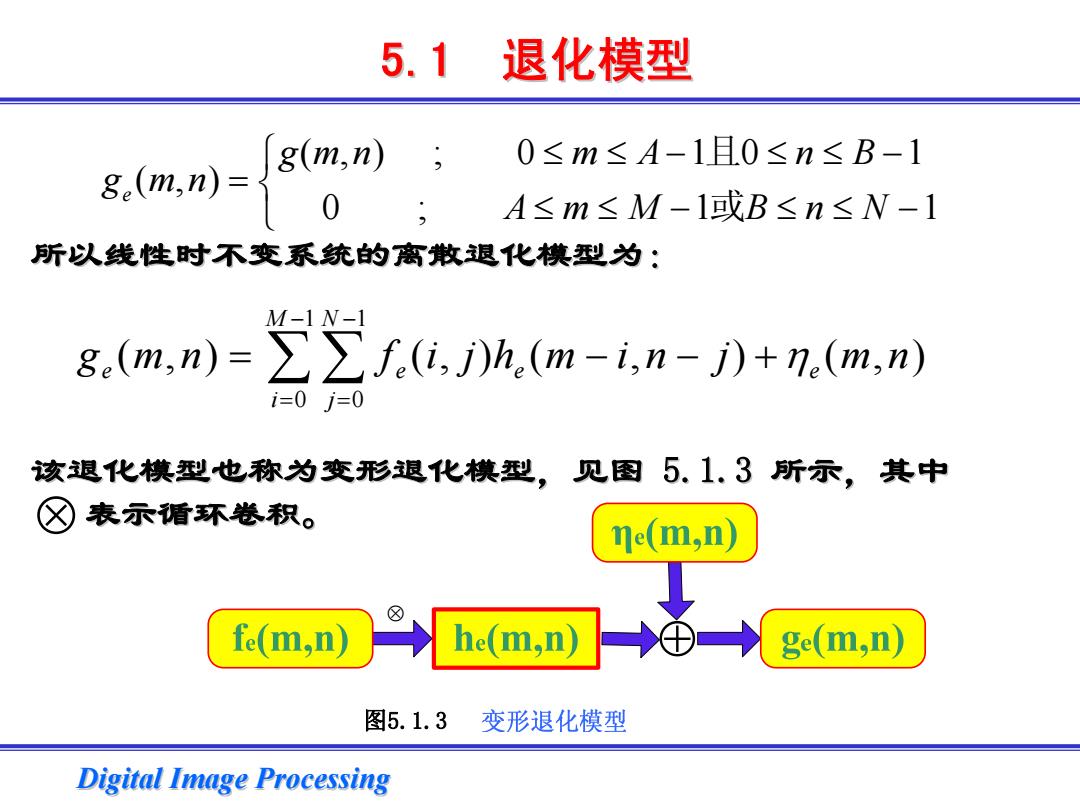
5.1退化模型 g(m,n) 0≤m≤A-1且0≤n≤B-1 g.(m.n)0 A≤m≤M-1或B≤n≤N-1 所以线性时不变系统的离散退化模型为: M-1N-1 ge(m,n)=∑∑f(,)h.(m-i,n-j)+n.(m,n) i=0j=0 该退化模型也称为变形退化模型,见图5.1.3所示,其中 表示循环卷积。 ne(m,n) fe(m,n) he(m,n) ge(m,n) 图5.1.3变形退化模型 Digital Image Processing
Digital Image Processing Digital Image Processing 所以线性时不变系统的离散退化模型为: 所以线性时不变系统的离散退化模型为: 该退化模型也称为变形退化模型,见图 该退化模型也称为变形退化模型,见图 5.1.3 所示,其中 表示循环卷积。 表示循环卷积。 (,) ; 0 1 0 1 (,) 0 ; 1 1 e gmn m A n B g mn AmM BnN ⎧ ≤ ≤− ≤≤ − = ⎨⎩ ≤ ≤ − ≤≤ − 且或 1 1 0 0 ( , ) (, ) ( , ) ( , ) M N e e e e i j g mn f i jh m in j mn η − − = = = − ∑ ∑ − + 5.1 退化模型 ⊕ ⊗ 图5.1.3 ⊗

5.1退化模型 离散退化模型还可以用矩阵描述 g=Hf+ 其中,f、g和门表示MN×1维的列向量,分别是由M×N维的矩 阵f(m,n以g(m,)和1(m,n)的各行堆积而成,如下所示: f(0,0) 8e(0,0) 7e(0,0) f(0,1) 8e(0,1) 7e(0,1) f(0,N-1) f= 8e(0,W-1) 7e(0,N-1) 8= f(1,0) 8e(1,0) 7= 7.(1,0) f(1,1) 8e(1,1) 7e(1,1) f(M-1,N-1) 8e(M-1,N-1) n(M-1,N-1) Digital Image Processing
Digital Image Processing Digital Image Processing 离散退化模型还可以用矩阵描述 离散退化模型还可以用矩阵描述 其中,f 、g和 表示MN×1维的列向量,分别是由 维的列向量,分别是由M×N维的矩 阵 、 和 的各行堆积而成,如下所示 的各行堆积而成,如下所示 : g = Hf + η (0,0) (0,1) (0, 1) (1, 0) (1,1) ( 1, 1) e e e e e e f f f N f f f fM N ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ − ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢⎣ − − ⎥⎦ # # (0,0) (0,1) (0, 1) (1, 0) (1,1) ( 1, 1) e e e e e e g g g N g g g gM N ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ − ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢⎣ − − ⎥⎦ # # (0,0) (0,1) (0, 1) (1,0) (1,1) ( 1, 1) e e e e e e N M N η η η η η η η ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ − ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢⎣ − − ⎥⎦ # # 5.1 退化模型 η e f (m,n) e g (m,n) ηe (m,n)

5.1退化模型 H为MN*N的矩阵,对于线性移不变系统具有如下特殊结构: H He He …H H H HiA …以 h.(i,0) h.(i,N-1)…h.(i,1) HE H 以 以 H, h.(i,1) h.(i,0) …h.(i,2) H= h.,N-)h6,N-2)…hi,0)w H4H2Hg…Hw 可以看出H是一个分块循环矩阵,而其中H也是右移循环 阵。这是由于在卷积时利用了[h]矩阵的周期延拓性。 Digital Image Processing
Digital Image Processing Digital Image Processing H为MN*MN的矩阵,对于线性移不变系统具有如下特殊结构: 的矩阵,对于线性移不变系统具有如下特殊结构: 可以看出H是一个分块循环矩阵,而其中 是一个分块循环矩阵,而其中Hi也是右移循环 阵。这是由于在卷积时利用了 阵。这是由于在卷积时利用了 矩阵的周期延拓性。 矩阵的周期延拓性。 0 1 -2 1 1 0 -1 2 210 3 123 0 M M M MMM M M HH H H H HH H HH H H H HHH H − −− − × ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ =⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ " " " # # # %# " ( ,0) ( , 1) ( ,1) ( ,1) ( ,0) ( ,2) ( , 1) ( , 2) ( ,0) ee e ee e i ee e N N h i h iN h i hi hi hi H hiN hiN hi × ⎡ − ⎤ ⎢ ⎥ =⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ − − ⎦ " " # # %# " e [h ] 5.1 退化模型

5.1退化模型 循环矩阵H的对角化 根据unt的结果,可以对H进行对角化,即H=WDW1 W是一个大小为MN X MN维的矩阵,由MXM个大小为NXN的子块 构成: wM(0,0) wM(0,1)) wM(0,M-1) wM(1,0) wM(1,1) wM(1,M-1) W= wM(M-1,O)wM(M-1,1)·wM(M-1,M-1) wu(i,m)=exp(j2rim/M), i,m=0,1,2,…,M-1 Wx(k,n)=exp(j2rkn/N), k,n=0,1,2,…,N-1 Digital Image Processing
Digital Image Processing Digital Image Processing 循环矩阵H的对角化 根据Hunt的结果,可以对 的结果,可以对H进行对角化,即 进行对角化,即 W是一个大小为MN×MN维的矩阵,由M×M个大小为N×N的子块 构成: -1 H = WDW (0,0) (0,1) (0, 1) (1,0) (1,1) (1, 1) ( 1,0) ( 1,1) ( 1, -1) MM M MM M MM M w w wM w w wM W wM wM wM M ⎡ ⎤ − ⎢ ⎥ − = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ −− − " " # ## # " ( , ) exp( 2 / ), w i m j im M M = π ( , ) exp( 2 / ), w kn N = j πkn N im M , 0,1, 2, , 1 = " − kn N , 0,1, 2, , 1 = " − 5.1 退化模型

5.1退化模型 从而 W=WM⑧WN={wM(i,m)}⑧{wN(k,n)} ={exp(j2πim/M)}⑧{exp(j2πnk/N)} D是一个对角矩阵 Dua-个aaN: i=k i≠k 式中[表示对。取喜,k©dN表示对N库k取家数。 由以上各式并结合: g=W DWf+n Digital Image Processing
Digital Image Processing Digital Image Processing 从而 D是一个对角矩阵 是一个对角矩阵 由以上各式并结合: 由以上各式并结合: ⎧⎪ • ⎨⎪⎩ ≠ k M N H([ ],k mod N) ; i = k D(k,i) = N0 ;i k -1 g = WDW f + η { (, )} { (,)} {exp( 2 / )} {exp( 2 / )} W W W w im w kn MN M N j π π im M j nk N =⊗= ⊗ = ⊗ 5.1 退化模型 式中 表示对 取整,k mod N表示对N除k取余数。 kN⎡ ⎤ ⎢ ⎥ ⎣ ⎦ kN