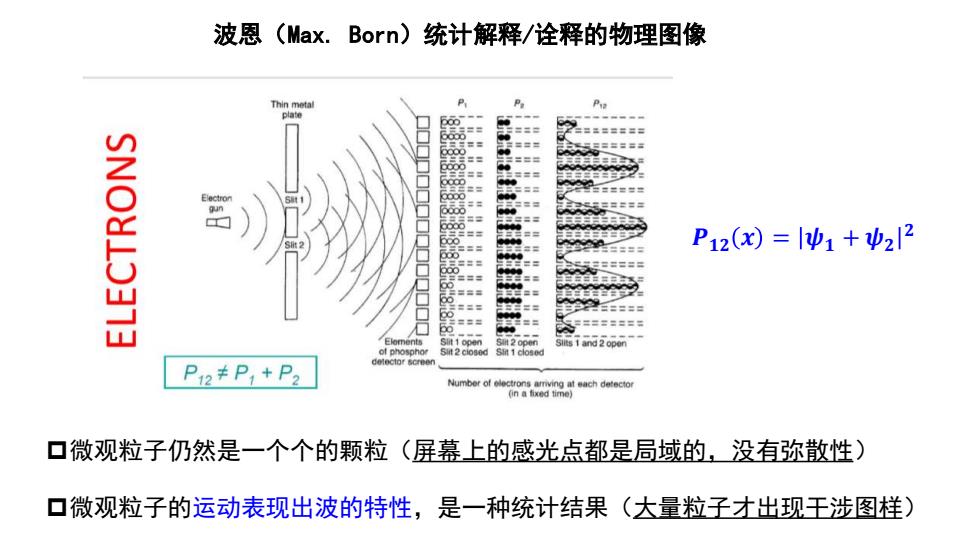
波恩(Max.Born)统计解释/诠释的物理图像 Thin meta P 里器世三三 P12(x)=1+ψ22 Elements Sut 2 ciosed and 2 opon detector scree P12≠P1+P2 Number of olectrons ariving at each detector (in a fixed time) 口微观粒子仍然是一个个的颗粒(屏幕上的感光点都是局域的,没有弥散性) ▣微观粒子的运动表现出波的特性,是一种统计结果(大量粒子才出现王涉图桂)
波恩(Max. Born)统计解释/诠释的物理图像 微观粒子仍然是一个个的颗粒(屏幕上的感光点都是局域的,没有弥散性) 微观粒子的运动表现出波的特性,是一种统计结果(大量粒子才出现干涉图样) 𝑷𝟏𝟐 𝒙 = 𝝍𝟏 + 𝝍𝟐 𝟐

口微观粒子的运动遵从统计因果,完全不同于经典理论的Laplace?决定性因果性。 粒子的运动由波函数妙描述,少不能准确地给出某个时刻粒子到达哪个位置,只能给出粒子可能到达地 点的一个统计分布,粒子的运动受到妙的向导,粒子出现在2大的地方,不会出现在2=0的地方, 德布罗意波实际上表示几率幅波。 Laplace决定论: 我们可以把宇宙现在的状态视为其过去的果以及未来的因。如果一个智者 (拉普拉斯)能知道某一刻所有自然运动的力和所有自然构成的物件的位置, 假如他也能够对这些数据进行分析,那么,宇宙里最大的物体到最小的粒子 的运动,都会包含在一条简单公式中。对于这智者来说没有事物会是含糊的, 而未来只会像过去那样出现在他面前。 Pierre-Simon Laplace 17491827
Pierre-Simon Laplace 1749–1827 Laplace决定论: 我们可以把宇宙现在的状态视为其过去的果以及未来的因。如果一个智者 (拉普拉斯)能知道某一刻所有自然运动的力和所有自然构成的物件的位置, 假如他也能够对这些数据进行分析,那么,宇宙里最大的物体到最小的粒子 的运动,都会包含在一条简单公式中。对于这智者来说没有事物会是含糊的, 而未来只会像过去那样出现在他面前。 微观粒子的运动遵从统计因果,完全不同于经典理论的Laplace决定性因果性。 粒子的运动由波函数𝜓描述,𝜓不能准确地给出某个时刻粒子到达哪个位置,只能给出粒子可能到达地 点的一个统计分布,粒子的运动受到𝜓的向导,粒子出现在 𝜓 2大的地方,不会出现在 𝜓 2 = 0的地方, 德布罗意波实际上表示几率幅波

口微观粒子的“粒子性”“不同于经典理论的粒子性,微观粒子的“波动性”也不 同于经典理论的波动性 统计解释表明,与微观粒子相联系的波是一种几率波,不是物理观测量,因此也就 不可能是某些物理量的空间分布;某个时刻微观粒子在空间哪个地方都有出现的几 率,因此不可能再有确定的运动轨道(这是经典粒子所特有的),Wh ich-Way实验 表明,确切知道粒子从哪个缝穿过,则没有干涉。 粒子性意味着:(1)有一定大小(定域的)、质量、电荷等一原子性或颗粒性 (2)没有确定的运动轨道 波动性意味着: (1)有干涉和衍射一叠加性 (2)不是某些物理量的空间分布呈周期性变化一非定域性
微观粒子的“粒子性”“不同于经典理论的粒子性,微观粒子的“波动性”也不 同于经典理论的波动性 粒子性意味着:(1)有一定大小(定域的)、质量、电荷等——原子性或颗粒性 (2)没有确定的运动轨道 波动性意味着:(1)有干涉和衍射——叠加性 (2)不是某些物理量的空间分布呈周期性变化——非定域性 统计解释表明,与微观粒子相联系的波是一种几率波,不是物理观测量,因此也就 不可能是某些物理量的空间分布;某个时刻微观粒子在空间哪个地方都有出现的几 率,因此不可能再有确定的运动轨道(这是经典粒子所特有的),Which-Way实验 表明,确切知道粒子从哪个缝穿过,则没有干涉

Note: ① 与经典力学相比,量子力学的功绩就是它成功地创造了一个客体(德布罗意几率幅 波业),在非相对论情况下(没有粒子的产生和湮灭),在几率幅波这个客体框架 内,巧妙而不矛盾地将粒子和波动的性质结合到了一起。 ② 量子力学中的几率不是无知的结果,这与经典力学中的几率不同。 在我们用经典力学处理抛硬币问题的时候,我们往往会说硬币的某一面会出现的 概率是多少,而无法明确到底哪一面会出现。这是因为我们不知道硬币的初始运动的 全部信息(速度、角速度等)和所有的外部影响(气流、硬币着陆的地面情况等)。 如果我们知道初始运动的全部信息,我们就会预言到底哪一面会出现。 量子力学中的几率不是缺少信息的结果,这种几率是真正的随机,并且没有进 一步的信息(所谓的隐变量)可以让事情不随机
Note: ① 与经典力学相比,量子力学的功绩就是它成功地创造了一个客体(德布罗意几率幅 波𝜓),在非相对论情况下(没有粒子的产生和湮灭),在几率幅波这个客体框架 内,巧妙而不矛盾地将粒子和波动的性质结合到了一起。 ② 量子力学中的几率不是无知的结果,这与经典力学中的几率不同。 在我们用经典力学处理抛硬币问题的时候,我们往往会说硬币的某一面会出现的 概率是多少,而无法明确到底哪一面会出现。这是因为我们不知道硬币的初始运动的 全部信息(速度、角速度等)和所有的外部影响(气流、硬币着陆的地面情况等)。 如果我们知道初始运动的全部信息,我们就会预言到底哪一面会出现。 量子力学中的几率不是缺少信息的结果,这种几率是真正的随机,并且没有进 一步的信息(所谓的隐变量)可以让事情不随机

平=Aear-m0 由于不能把粒子归结为处在一个严格的位置上,人们只能 确定在一定预期找到粒子的几率,在空间dv内粒子出现的几率 可有几率密度引妙(行,t)2对体积的积分给出 P(v(.Pdxdydz p=(行,t)表示在单位体积内找到粒子的几率一几率密度 在非相对论情况下(没有粒子的产生和湮灭),在整个空间找 到粒子的几率为1 l(行,t)12dv=1 波函数的归一化条件 -00
由于不能把粒子归结为处在一个严格的位置上,人们只能 确定在一定预期找到粒子的几率,在空间dv内粒子出现的几率 可有几率密度 𝜓 𝑟 Ԧ ,𝑡 2对体积的积分给出 P = න 𝜓 𝑟 Ԧ ,𝑡 2dv = න 𝜓 𝑟 Ԧ ,𝑡 2d𝑥dydz ρ = 𝜓 𝑟 Ԧ ,𝑡 2表示在单位体积内找到粒子的几率——几率密度 在非相对论情况下(没有粒子的产生和湮灭),在整个空间找 到粒子的几率为1 P = න −∞ +∞ 𝜓 𝑟 Ԧ ,𝑡 2dv = 1 波函数的归一化条件