
第二章二次量子化
第二章 二次量子化

●全同多粒子体系难以用通常的波函数处理 →发展了二次量子化方法心 引入粒子占有数表象一用各单粒子态填充 的粒子数描述状态;交换对称性自动满足 十基本算符:粒子的产生算符和湮灭算符 十任意态矢和力学量均可用它们表示 十有系统的法则计算力学量的矩阵元
●全同多粒子体系引难以用通常的波函数处理 言 →发展了二次量子化方法☻ † 引入粒子占有数表象—用各单粒子态填充 的粒子数描述状态;交换对称性自动满足 † 基本算符:粒子的产生算符和湮灭算符 † 任意态矢和力学量均可用它们表示 † 有系统的法则计算力学量的矩阵元

§2.1全同粒子体系的量子态描述
§2.1 全同粒子体系的量子态描述

●为什么要引入粒子数表象? 1.全同粒子的交换对称性 何为全同粒子? 2.全同性与量子化的概念→区别于经典
●为什么要引入粒子数表象? 1. 全同粒子的交换对称性 何为全同粒子? 2. 全同性与量子化的概念→区别于经典
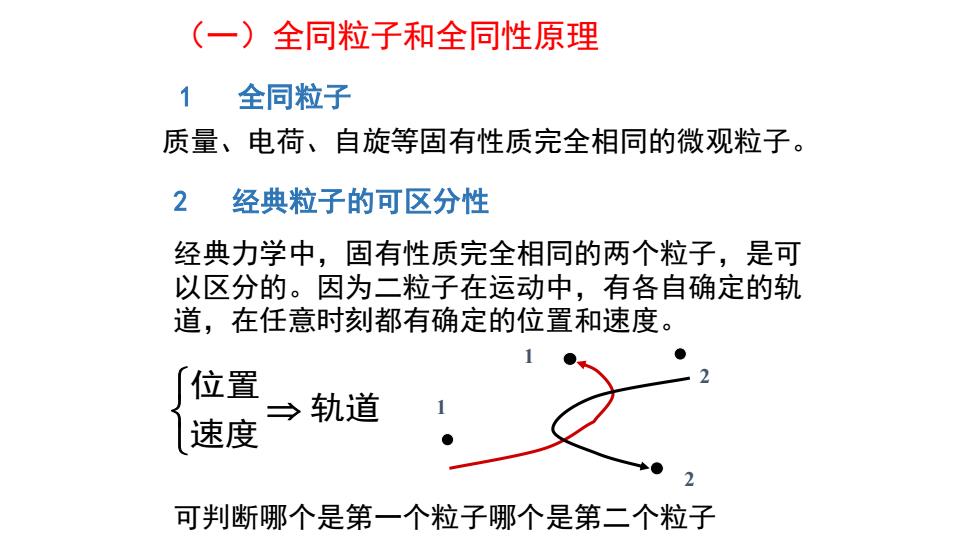
(一)全同粒子和全同性原理 1全同粒子 质量、电荷、自旋等固有性质完全相同的微观粒子。 2 经典粒子的可区分性 经典力学中,固有性质完全相同的两个粒子,是可 以区分的。因为二粒子在运动中,有各自确定的轨 道,在任意时刻都有确定的位置和速度。 1 位置 →轨道 速度 可判断哪个是第一个粒子哪个是第二个粒子
1 全同粒子 质量、电荷、自旋等固有性质完全相同的微观粒子。 2 经典粒子的可区分性 经典力学中,固有性质完全相同的两个粒子,是可 以区分的。因为二粒子在运动中,有各自确定的轨 道,在任意时刻都有确定的位置和速度。 位置 轨道 速度 可判断哪个是第一个粒子哪个是第二个粒子 1 2 1 2 (一)全同粒子和全同性原理