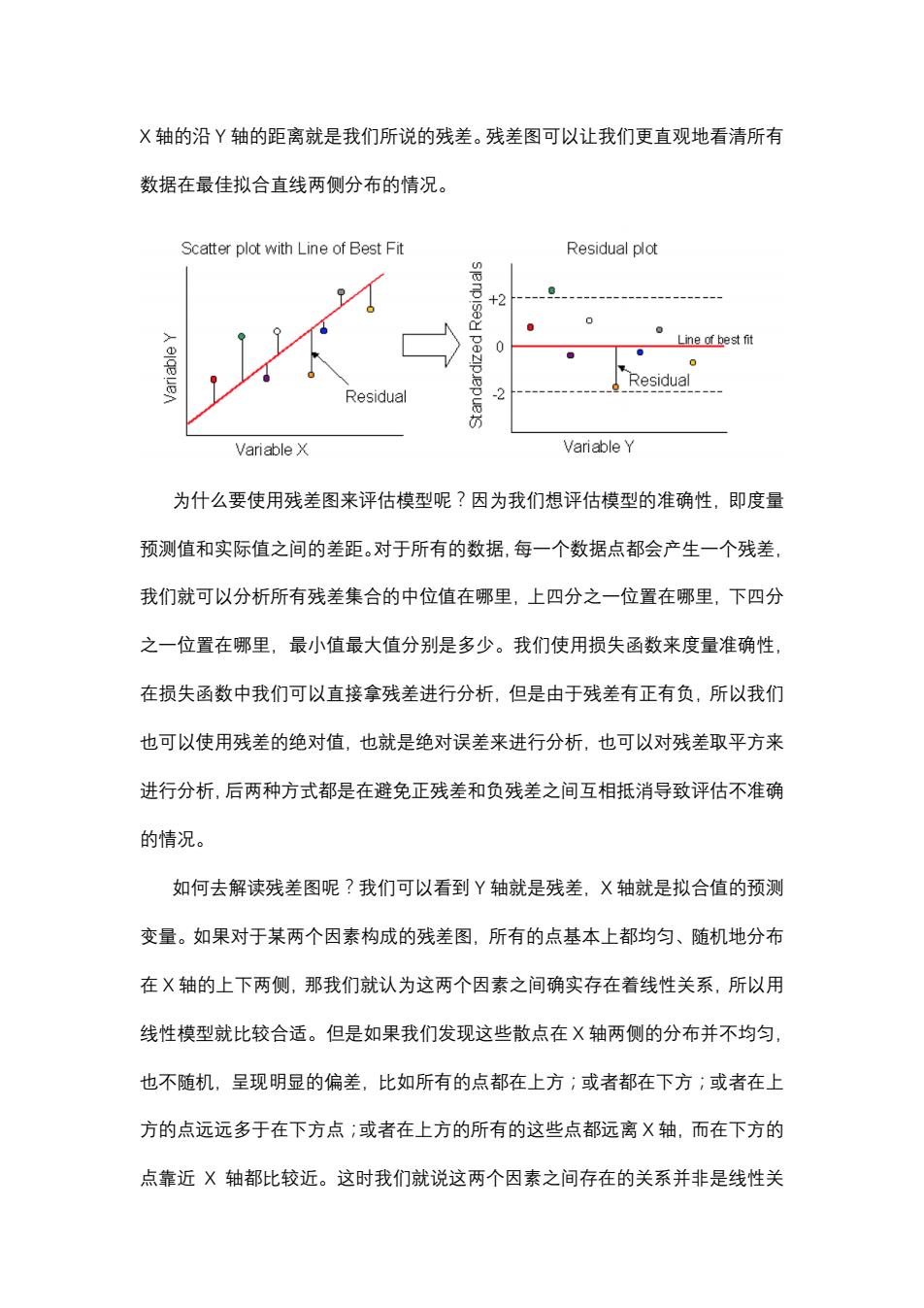
X轴的沿Y轴的距离就是我们所说的残差。残差图可以让我们更直观地看清所有 数据在最佳拟合直线两侧分布的情况。 Scatter plot with Line of Best Fit Residual plot spenp +2 Line of best fit pezip.epu 0 0 Residual Residual Variable X Variable Y 为什么要使用残差图来评估模型呢?因为我们想评估模型的准确性,即度量 预测值和实际值之间的差距。对于所有的数据,每一个数据点都会产生一个残差, 我们就可以分析所有残差集合的中位值在哪里,上四分之一位置在哪里,下四分 之一位置在哪里,最小值最大值分别是多少。我们使用损失函数来度量准确性, 在损失函数中我们可以直接拿残差进行分析,但是由于残差有正有负,所以我们 也可以使用残差的绝对值,也就是绝对误差来进行分析,也可以对残差取平方来 进行分析,后两种方式都是在避免正残差和负残差之间互相抵消导致评估不准确 的情况。 如何去解读残差图呢?我们可以看到Y轴就是残差,X轴就是拟合值的预测 变量。如果对于某两个因素构成的残差图,所有的点基本上都均匀、随机地分布 在X轴的上下两侧,那我们就认为这两个因素之间确实存在着线性关系,所以用 线性模型就比较合适。但是如果我们发现这些散点在X轴两侧的分布并不均匀, 也不随机,呈现明显的偏差,比如所有的点都在上方;或者都在下方;或者在上 方的点远远多于在下方点;或者在上方的所有的这些点都远离X轴,而在下方的 点靠近X轴都比较近。这时我们就说这两个因素之间存在的关系并非是线性关
X 轴的沿 Y 轴的距离就是我们所说的残差。残差图可以让我们更直观地看清所有 数据在最佳拟合直线两侧分布的情况。 为什么要使用残差图来评估模型呢?因为我们想评估模型的准确性,即度量 预测值和实际值之间的差距。对于所有的数据,每一个数据点都会产生一个残差, 我们就可以分析所有残差集合的中位值在哪里,上四分之一位置在哪里,下四分 之一位置在哪里,最小值最大值分别是多少。我们使用损失函数来度量准确性, 在损失函数中我们可以直接拿残差进行分析,但是由于残差有正有负,所以我们 也可以使用残差的绝对值,也就是绝对误差来进行分析,也可以对残差取平方来 进行分析,后两种方式都是在避免正残差和负残差之间互相抵消导致评估不准确 的情况。 如何去解读残差图呢?我们可以看到 Y 轴就是残差,X 轴就是拟合值的预测 变量。如果对于某两个因素构成的残差图,所有的点基本上都均匀、随机地分布 在 X 轴的上下两侧,那我们就认为这两个因素之间确实存在着线性关系,所以用 线性模型就比较合适。但是如果我们发现这些散点在 X 轴两侧的分布并不均匀, 也不随机,呈现明显的偏差,比如所有的点都在上方;或者都在下方;或者在上 方的点远远多于在下方点;或者在上方的所有的这些点都远离 X 轴,而在下方的 点靠近 X 轴都比较近。这时我们就说这两个因素之间存在的关系并非是线性关

系,我们用其他的非线性模型来进行分析就会显得更合适。 在Python中如何来做线性回归的残差分析吗?下面是一段脚本,我们简单 解释一下。 test_x=np.asanyarray(test[['ENGINESIZE']] test y=np.asanyarray(test[['CO2EMISSIONS']] test_y_=regr.predict(test_x) print("Residual sum of squares:8.2f" snp.mean((test_y_-test_y)**2)) Explained variance score:1 is perfect prediction print('variance score:8.2f'®r.score(test_x,test_y)) plot outputs plt.scatter(test_x,test_y,color='blue') plt.plot(test_x,test_y_color='black',linewidth=3) plt.xlabel("Engine size") plt.ylabel("Emission") plt.show() Residual sum of squares:874.93 Variance score:0.81 之前我们就提到过数据集分成了训练集和测试集,我们使用测试集来进行评 估。首先,我们获取测试集中发动机的大小和二氧化碳排放量这两个数据列的数 据,数据集分别是test_y和test_x。然后,我们用训练出来的模型,也就是说我 们的线性回归模型来预测二氧化碳排放量,所以调用了线性回归对象上的预测方 法,传递了test×数据集,得到了一个新的预测集,就是test_y_,注意它又加了 一个下划线,和刚才我们看到实测值test_y是不一样的。然后,我们用test_y.预 测值减去tsty实际观测值,得到一个残差数据集。对于每一个残差求平方,然 后取它的平均数,我们就知道了残差的平均值。之后,我们可以绘制散点图,对 实际观测到的数据,也就是test×和test_y,用蓝色的圆点来绘制,然后绘制一 条线性回归线,也就是对test_x和test_y_,用黑色的颜色来绘制一条宽度为3的 线性回归线。这样我们就能得到一张回归图。通过这样的分析,我们就可以得知 这二者之间是否存在相关关系,以及它们的相关度是多少
系,我们用其他的非线性模型来进行分析就会显得更合适。 在 P瀌瀇濻瀂瀁 中如何来做线性回归的残差分析吗?下面是一段脚本,我们简单 解释一下。 之前我们就提到过数据集分成了训练集和测试集,我们使用测试集来进行评 估。首先,我们获取测试集中发动机的大小和二氧化碳排放量这两个数据列的数 据,数据集分别是 瀇濸瀆瀇_瀌 和 瀇濸瀆瀇_瀋。然后,我们用训练出来的模型,也就是说我 们的线性回归模型来预测二氧化碳排放量,所以调用了线性回归对象上的预测方 法,传递了 瀇濸瀆瀇_瀋 数据集,得到了一个新的预测集,就是 瀇濸瀆瀇_瀌_,注意它又加了 一个下划线,和刚才我们看到实测值 瀇濸瀆瀇_瀌 是不一样的。然后,我们用 瀇濸瀆瀇_瀌_预 测值减去 瀇濸瀆瀇_瀌 实际观测值,得到一个残差数据集。对于每一个残差求平方,然 后取它的平均数,我们就知道了残差的平均值。之后,我们可以绘制散点图,对 实际观测到的数据,也就是 瀇濸瀆瀇_瀋 和 瀇濸瀆瀇_瀌,用蓝色的圆点来绘制,然后绘制一 条线性回归线,也就是对 瀇濸瀆瀇_瀋 和 瀇濸瀆瀇_瀌_,用黑色的颜色来绘制一条宽度为 3 的 线性回归线。这样我们就能得到一张回归图。通过这样的分析,我们就可以得知 这二者之间是否存在相关关系,以及它们的相关度是多少

四、回归分析案例 让我们通过一个notebook来看一看线性回归。我们使用的数据集就是前面 提到的汽车的二氧化碳排放量和汽车指标之间的关系的数据集。我们把这个数据 集分成训练集和测试集,用训练集训练模型,用测试集评估模型。 首先,我们要加载所需要的库,然后可以去下载这个数据集,下载好以后装 载它。下载数据的数据集中包含了汽车的各种各样的技术指标以及汽车的二氧化 碳排放量。我们加载数据,看一看这个数据集,看到数据集里面包括了汽车各种 各样的参数,包括它的制造商、发动机的大小、气缸数、百公里油耗以及二氧化 碳排放量。 n【2]i urces/data/ #take a look at the dataset df.head Out[2): MODELYEAR MAKE MODEL VEHICLECLASS ENGINESIZE CYLINDERS TRANSMISSION FUELTYPE FUELCONSUMPTION_CITY FUELCON 02014 ACURA ILX COMPACT 2.0 4 AS5 9.9 6.7 12014 ACURA ILX COMPACT 24 M6 112 7.7 IX 2014 ACURA HYBRID COMPACT 1.5 60 5.8 2014 ACURA MDX SUV-SMALL 3.5 12.7 4WD AS6 97 RDX 2014 ACURA 3.5 AWD SUV-SMALL AS6 和往常一样,我们可以探索一下这个数据。首先, 我们得到所有数值型数据 列上的汇总,包括了行数、平均值、标准差等等,这是我们非常熟悉的内容。 1decbha Out[3]: MODELYEAR ENGINESIZE CYLINDERS FUELCONSUMPTION_CITY FUELCONSUMPTION_HWY FUELCONSUMPTION_COMB FUELCON: count 1067.0 1067.0000001087.0000001087,000000 1067.000000 1067.000000 1067.00000 mean2014.0 3.346298 5,794752 13298532 9.474602 11.580BBt 26.441425 std 0.0 1.415895 1,797447 4.101253 2.794510 3.485595 7.488702 min 2014.0 1.000000 3.000000 4.600000 4.00000 4.700000 11.000000 25%2014.0 2.000000 4.000000 10.250000 7.500000 g.000000 21.000000 50%2014.0 3.400000 6.000000 12.600000 8.800000 10.900000 26.000000 75%2014.0 4.300000 8.000000 15.550000 10.850000 13.350000 31.000000 max2014.0 8.40000012.00000030200000 20.500000 25.800000 60.000000 我们可以取出我们认为跟汽车二氧化碳排放量相关的这些列来看一看。我们 认为发动机的大小、气缸数和百公里综合油耗与二氧化碳排放量相关,所以我们
四、回归分析案例 让我们通过一个 瀁瀂瀇濸濵瀂瀂濾 来看一看线性回归。我们使用的数据集就是前面 提到的汽车的二氧化碳排放量和汽车指标之间的关系的数据集。我们把这个数据 集分成训练集和测试集,用训练集训练模型,用测试集评估模型。 首先,我们要加载所需要的库,然后可以去下载这个数据集,下载好以后装 载它。下载数据的数据集中包含了汽车的各种各样的技术指标以及汽车的二氧化 碳排放量。我们加载数据,看一看这个数据集,看到数据集里面包括了汽车各种 各样的参数,包括它的制造商、发动机的大小、气缸数、百公里油耗以及二氧化 碳排放量。 和往常一样,我们可以探索一下这个数据。首先,我们得到所有数值型数据 列上的汇总,包括了行数、平均值、标准差等等,这是我们非常熟悉的内容。 我们可以取出我们认为跟汽车二氧化碳排放量相关的这些列来看一看。我们 认为发动机的大小、气缸数和百公里综合油耗与二氧化碳排放量相关,所以我们

看看这三列的数据。实际上它们和二氧化碳排放量之间确实存在着正相关关系, 但是这三列跟它的关联度又不一样,所谓的关联程度存在着差异。我们可以看一 下这些列画出来的直方图的差异。 In [4]:cdf-dE[['ENGINESIZE','CYLINDERS','FUELCONSUMPTION_COMB','CO2EMISSIONS'] cdf.head() out4]:「 ENGINESIZE CYLINDERS FUELCONSUMPTION_COMB CO2EMISSIONS 02.0 8.5 198 12.4 9.6 221 21.5 136 335 6 11.1 255 43.5 10.6 244 In [5]:viz-cdf[['CYLINDERS','ENGINESI8E','CO2EMISSIONS','FUELCONSUMPTION_COMB'] ple.() CO2EMISSIONS CYUNDERS 00 5 然后可以用散点图来看一看,将我们认为与二氧化碳排放量相关的三列和二 氧化碳排放量之间的关系用散点图来描述。下面是汽车百公里综合油耗和二氧化 碳排放量之间的关系,我们看到它就像三条直线一样,说明它们确实存在着线性 关系。 In [6]:plt.scatter(cdf.PUgLCONSUNPTION COMB,cdf.Co2EMISSIONS,color-'blue') plt.xlabel('FUELCONSUMPTION CONB") plt.ylabel("gmission") plt.show() 500 50 480 下面是发动机大小和二氧化碳排放量之间的关系,我们看到它整体有一个线 性关系的趋势,也就是发动机的大小越大,二氧化碳排放量越大
看看这三列的数据。实际上它们和二氧化碳排放量之间确实存在着正相关关系, 但是这三列跟它的关联度又不一样,所谓的关联程度存在着差异。我们可以看一 下这些列画出来的直方图的差异。 然后可以用散点图来看一看,将我们认为与二氧化碳排放量相关的三列和二 氧化碳排放量之间的关系用散点图来描述。下面是汽车百公里综合油耗和二氧化 碳排放量之间的关系,我们看到它就像三条直线一样,说明它们确实存在着线性 关系。 下面是发动机大小和二氧化碳排放量之间的关系,我们看到它整体有一个线 性关系的趋势,也就是发动机的大小越大,二氧化碳排放量越大
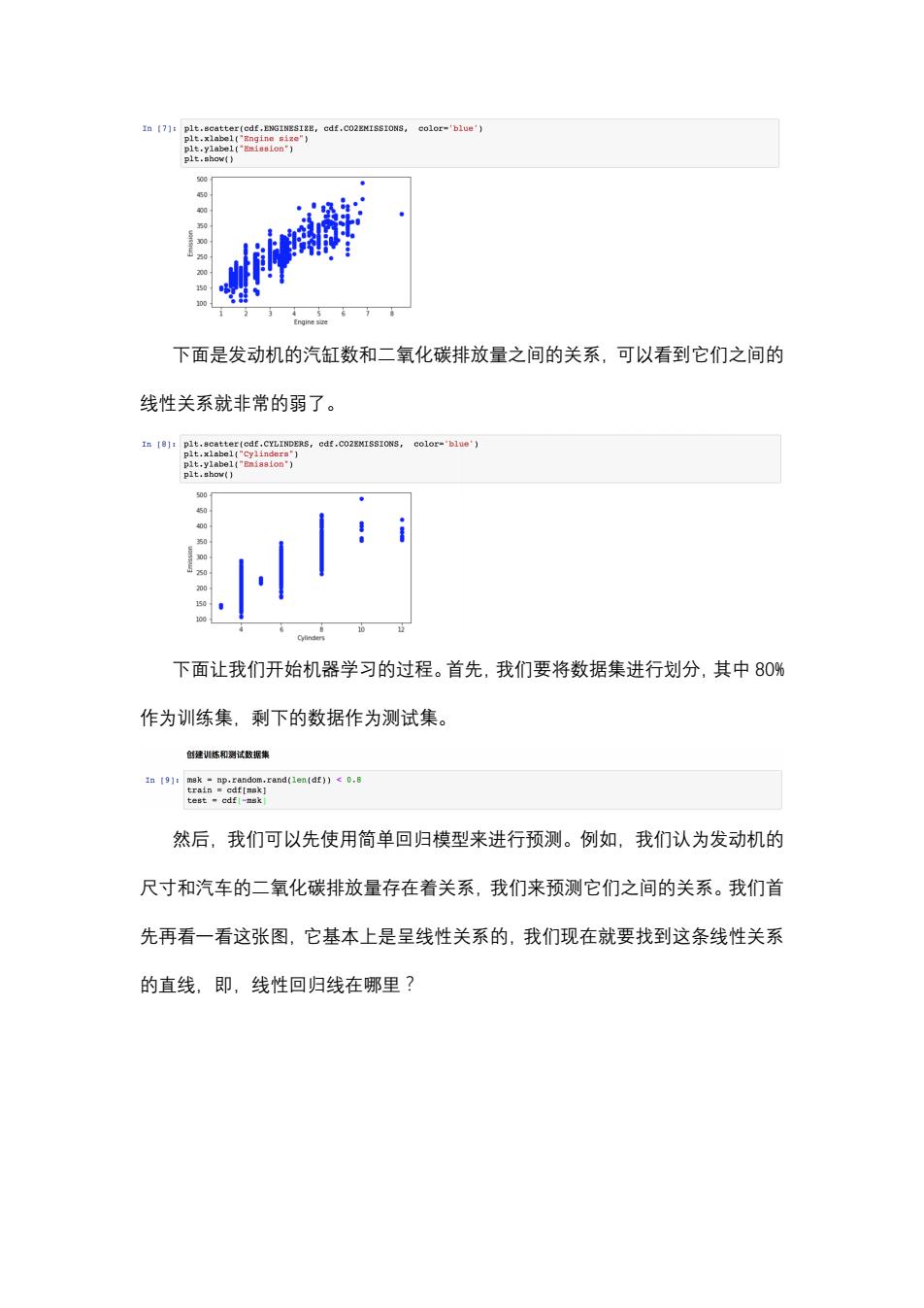
In (7]:plt.scatter(edf.EMGINESI2E,cdf.C02ENISSIONS, color-'blue') plt.xlabel("Engine size") p1t,y1ae1('mi881on“) plt.show() 0 430 下面是发动机的汽缸数和二氧化碳排放量之间的关系,可以看到它们之间的 线性关系就非常的弱了。 In [8]:plt.scatter(edf.CYLINDERS,cdf.Co2EMISSIONS, color-'blue') plt.xlabel("Cylinders"l plt.ylabel("Emission') plt.show() 500 450 50 10 下面让我们开始机器学习的过程。首先,我们要将数据集进行划分,其中80% 作为训练集,剩下的数据作为测试集。 创建训练和测试数据集 In 19]:mak np.random.rand(len(df))<0.8 train cdf[nsk] test cdf[-nsk 然后,我们可以先使用简单回归模型来进行预测。例如,我们认为发动机的 尺寸和汽车的二氧化碳排放量存在着关系,我们来预测它们之间的关系。我们首 先再看一看这张图,它基本上是呈线性关系的,我们现在就要找到这条线性关系 的直线,即,线性回归线在哪里?
下面是发动机的汽缸数和二氧化碳排放量之间的关系,可以看到它们之间的 线性关系就非常的弱了。 下面让我们开始机器学习的过程。首先,我们要将数据集进行划分,其中 80% 作为训练集,剩下的数据作为测试集。 然后,我们可以先使用简单回归模型来进行预测。例如,我们认为发动机的 尺寸和汽车的二氧化碳排放量存在着关系,我们来预测它们之间的关系。我们首 先再看一看这张图,它基本上是呈线性关系的,我们现在就要找到这条线性关系 的直线,即,线性回归线在哪里?