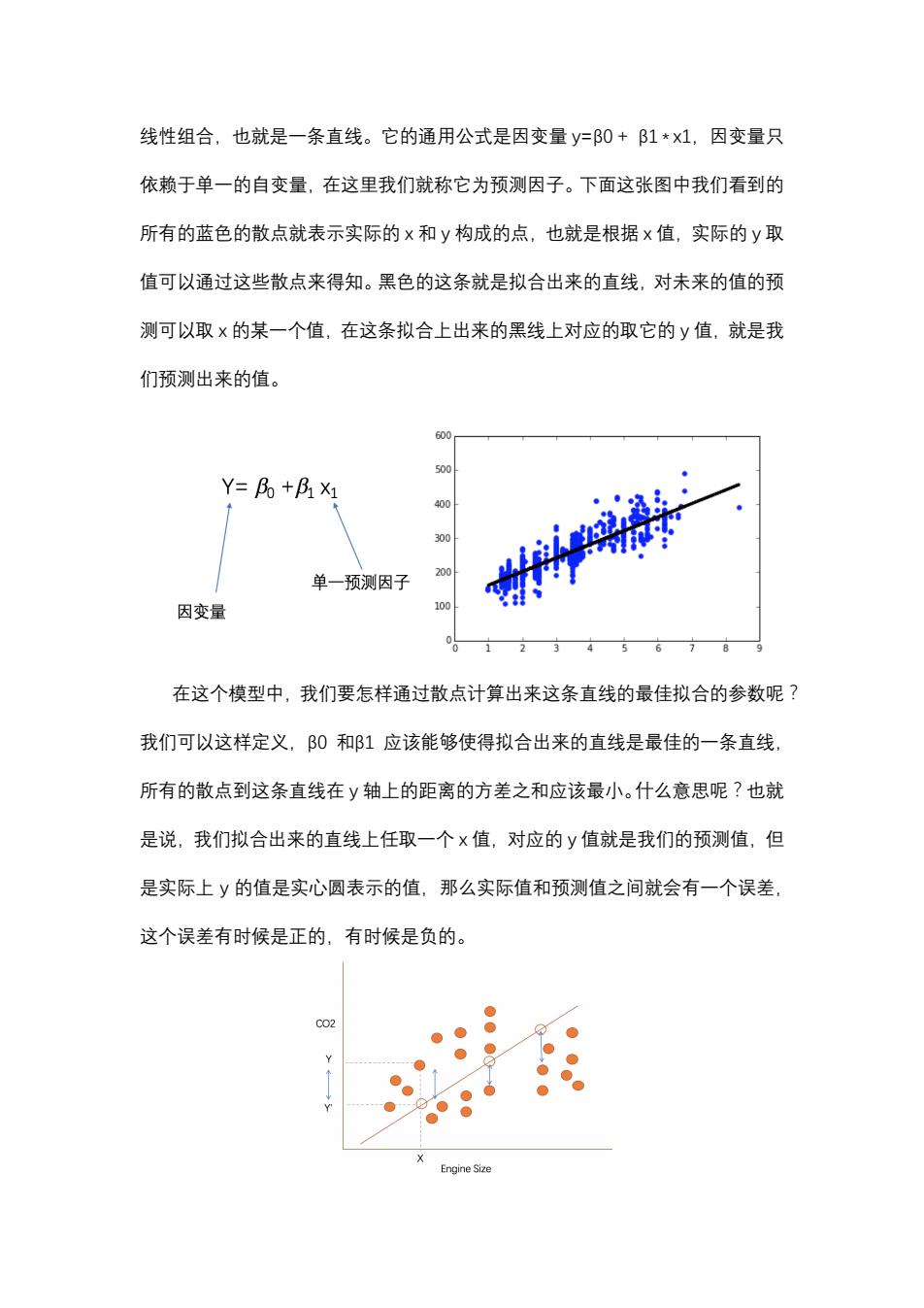
线性组合,也就是一条直线。它的通用公式是因变量y=β0+B1*x1,因变量只 依赖于单一的自变量,在这里我们就称它为预测因子。下面这张图中我们看到的 所有的蓝色的散点就表示实际的x和y构成的点,也就是根据x值,实际的y取 值可以通过这些散点来得知。黑色的这条就是拟合出来的直线,对未来的值的预 测可以取x的某一个值,在这条拟合上出来的黑线上对应的取它的y值,就是我 们预测出来的值。 500 Y=Bo+B1 X1 400 300 单一预测因子 200 因变量 100 在这个模型中,我们要怎样通过散点计算出来这条直线的最佳拟合的参数呢? 我们可以这样定义,B0和β1应该能够使得拟合出来的直线是最佳的一条直线, 所有的散点到这条直线在y轴上的距离的方差之和应该最小。什么意思呢?也就 是说,我们拟合出来的直线上任取一个x值,对应的y值就是我们的预测值,但 是实际上y的值是实心圆表示的值,那么实际值和预测值之间就会有一个误差, 这个误差有时候是正的,有时候是负的。 C02 Engine Size
线性组合,也就是一条直线。它的通用公式是因变量 瀌=β0 + β1 * 瀋1,因变量只 依赖于单一的自变量,在这里我们就称它为预测因子。下面这张图中我们看到的 所有的蓝色的散点就表示实际的 瀋 和 瀌 构成的点,也就是根据 瀋 值,实际的 瀌 取 值可以通过这些散点来得知。黑色的这条就是拟合出来的直线,对未来的值的预 测可以取 瀋 的某一个值,在这条拟合上出来的黑线上对应的取它的 瀌 值,就是我 们预测出来的值。 在这个模型中,我们要怎样通过散点计算出来这条直线的最佳拟合的参数呢? 我们可以这样定义,β0 和β1 应该能够使得拟合出来的直线是最佳的一条直线, 所有的散点到这条直线在 瀌 轴上的距离的方差之和应该最小。什么意思呢?也就 是说,我们拟合出来的直线上任取一个 瀋 值,对应的 瀌 值就是我们的预测值,但 是实际上 瀌 的值是实心圆表示的值,那么实际值和预测值之间就会有一个误差, 这个误差有时候是正的,有时候是负的

为了表示这条直线能够最好地拟合所有的点,我们把这些正误差和负误差通 通平方一下,然后累加,方差和最小的那条直线,就是拟合最好的直线,所以实 际上在这里我们用到了最小二乘法。最小二乘法的数学描述就是把所有的β值表 示成一个向量,如果每一个实际的y的取值与通过x的取值与β向量的乘积产生 的预测值之间的方差累加起来最小,那么这就是我们要找得这条向量,所以我们 可以看到最佳拟合直线产生的残值残差平方和是最小的。 MIN) 怎样计算简单线性模型中的β向量呢?下面是最小二乘法给出的计算公式, 用每一个x的值与x的平均值的差和y的值与y的平均值的差的积累加起来,除 以×与x的平均值的方差的累加和就得到了B1。B0是基于B1计算的,它等于y 的平均值减去β1乘以×的平均值。它的数学原理在这里我们就不用去深究了。 感兴趣的同学可以自己去查看它的证明和推导过程。 B。=y-月x 为什么不用深究呢?因为Python已经帮我们把这些功能实现了。例如,下 面是一个通过最小二乘法来计算刚才我们看到的β0和β1的脚本。首先,我们从 sklearn这个库里面导入线性模型,然后在线性模型这个对象上获取线性回归模 型对象。我们抽取训练集当中的两列:发动机的大小和二氧化碳的排放量,分别 放到train_x、train_y中,然后调用刚才的线性回归模型对象上的ft方法,传递 进去自变量数组和因变量数组,也就是train_x、train_y,那么它就会自动地帮我 们计算出来相应的β0和β1,也就是说它会自动地产生拟合出来的直线。我们最 后可以通过两个print的方法得到β1是38.68021623,而β0,也就是截距,是
为了表示这条直线能够最好地拟合所有的点,我们把这些正误差和负误差通 通平方一下,然后累加,方差和最小的那条直线,就是拟合最好的直线,所以实 际上在这里我们用到了最小二乘法。最小二乘法的数学描述就是把所有的β值表 示成一个向量,如果每一个实际的 瀌 的取值与通过 瀋 的取值与β向量的乘积产生 的预测值之间的方差累加起来最小,那么这就是我们要找得这条向量,所以我们 可以看到最佳拟合直线产生的残值残差平方和是最小的。 怎样计算简单线性模型中的β向量呢?下面是最小二乘法给出的计算公式, 用每一个 瀋 的值与 瀋 的平均值的差和 瀌 的值与 瀌 的平均值的差的积累加起来,除 以 瀋 与 瀋 的平均值的方差的累加和就得到了β1。β0 是基于β1 计算的,它等于 瀌 的平均值减去β1 乘以 瀋 的平均值。它的数学原理在这里我们就不用去深究了。 感兴趣的同学可以自己去查看它的证明和推导过程。 为什么不用深究呢?因为 P瀌瀇濻瀂瀁 已经帮我们把这些功能实现了。例如,下 面是一个通过最小二乘法来计算刚才我们看到的β0 和β1 的脚本。首先,我们从 瀆濾濿濸濴瀅瀁 这个库里面导入线性模型,然后在线性模型这个对象上获取线性回归模 型对象。我们抽取训练集当中的两列:发动机的大小和二氧化碳的排放量,分别 放到 瀇瀅濴濼瀁_瀋、瀇瀅濴濼瀁_瀌 中,然后调用刚才的线性回归模型对象上的 濹濼瀇 方法,传递 进去自变量数组和因变量数组,也就是 瀇瀅濴濼瀁_瀋、瀇瀅濴濼瀁_瀌,那么它就会自动地帮我 们计算出来相应的β0 和β1,也就是说它会自动地产生拟合出来的直线。我们最 后可以通过两个 瀃瀅濼瀁瀇 的方法得到β1 是 38.68021623,而β0,也就是截距,是

126.61208813,所以通过Python的线性回归对象调用其fit方法,就可以帮我们 自动去拟合出来两个数据集之间的线性关系。 from sklearn import linear model regr linear model.LinearRegression() train_x=np.asanyarray(train[['ENGINESIZE']] train y=np.asanyarray(train[['CO2EMISSIONS']] regr.fit (train x,train y) The coefficients print 'Coefficients:'regr.coef print 'Intercept:',regr.intercept Coefficients:[38.68021623]] Intercept:[126,61208813] 如果自变量有多个,那就是一个多元线性回归,也就是y=B0+B1*x1+B 2*x2++Bn*n,其中y仍然是因变量,x1到n是自变量,B1到Bn是对 应的自变量的系数,B0是截距。每一个跟自变量相关的系数都表示了这个自变 量与因变量之间的关系,即如果要是大于零,说明它们是正相关的,如果要是 小于零,说明它们是负相关的,如果等于0,就表示它们不相关。怎么才能找到 合适的值呢?可以通过最小二乘法的扩展来计算出来从B0到β的值,甚至有许 多不是线性函数的非线性函数也可以转换成上面的形式来计算,具体的数学推导 我们这里就不在深入讨论了,因为Python同样可以帮我们做好。我们可以举个 例子,假设我们认为汽车的功率、重量、发动机尺寸和在高速公路上的百公里综 合油耗与汽车的售价之间存在着关联关系,这是一个典型的多元线性回归模型。 z df[['horsepower','curb-weight','engine-size','highway-mpg'] Fit the linear model using the four above-mentioned variables. multi_fit 1m.fit(2,df['price']) multi fit LinearRegression(copy_X=True,fit_intercept=True,n_jobs=1,normalize=False) 现在的因变量是汽车的价格,而它的自变量包含了四个变量,我们可以通过 线性回归的函数给出相应的结果,我们将数据集这四列装载到一个叫z的数据集
126.61208813,所以通过 P瀌瀇濻瀂瀁 的线性回归对象调用其 濹濼瀇 方法,就可以帮我们 自动去拟合出来两个数据集之间的线性关系。 如果自变量有多个,那就是一个多元线性回归,也就是 瀌=β0 + β1 * 瀋1 + β 2 * 瀋2 + … + β瀁 * 瀋瀁,其中 瀌 仍然是因变量,瀋1 到 瀋瀁 是自变量,β1 到β瀁 是对 应的自变量的系数,β0 是截距。每一个跟自变量相关的系数都表示了这个自变 量与因变量之间的关系,即β濼 如果要是大于零,说明它们是正相关的,如果要是 小于零,说明它们是负相关的,如果等于 0,就表示它们不相关。怎么才能找到 合适的值呢?可以通过最小二乘法的扩展来计算出来从β0 到β瀁 的值,甚至有许 多不是线性函数的非线性函数也可以转换成上面的形式来计算,具体的数学推导 我们这里就不在深入讨论了,因为 P瀌瀇濻瀂瀁 同样可以帮我们做好。我们可以举个 例子,假设我们认为汽车的功率、重量、发动机尺寸和在高速公路上的百公里综 合油耗与汽车的售价之间存在着关联关系,这是一个典型的多元线性回归模型。 现在的因变量是汽车的价格,而它的自变量包含了四个变量,我们可以通过 线性回归的函数给出相应的结果,我们将数据集这四列装载到一个叫 瀍 的数据集

中,然后通过调用拟合函数找到自变量z数据集与因变量price数据集之间的关 系,我们就可以得到它算出来的截距以及在四个变量上的β值。最后我们可以得 到pice和这四个参数之间的线性模型,这就是我们看到的最终的结果。 1m.intercept_ -15678,742628061467 lm.coef_ array([52.65851272, 4.69878948,81.95906216,33.58258185]) Price =-15678.74 +(52.66)horsepower +(4.70)*curb-weight +(81.96)* engine-size +(33.58)*highway-mpg 如果回归的时候我们发现对应的模型不是线性模型怎么办?例如,像多项式 函数描述的非线性的模型该如何处理?假设y=β0+B1*×+B2*xA2+β3* x八3,这时我们看到的,出现了高次(X平方和×立方),说明这个模型就不是线性 模型。这时在数学上的处理是引入新的变量,将x2和3引入,分别表示x平方 和x立方,把整个上面的公式就转换成了一个新的多元线性回归模型y=β0+ B1*X+β2*x2+B3*x3,通过这种方式来解决。 三、模型评估和可视化 我们是通过可视化来评估模型的。我们为什么要评估模型,原因是因为我们 想知道开发出来的模型能不能用做预测模型来预测未来的值。在评估的时候,我
中,然后通过调用拟合函数找到自变量 瀍 数据集与因变量 瀃瀅濼濶濸 数据集之间的关 系,我们就可以得到它算出来的截距以及在四个变量上的β值。最后我们可以得 到 瀃瀅濼濶濸 和这四个参数之间的线性模型,这就是我们看到的最终的结果。 P瀅濼濶濸 = -15678.74 + (52.66 ) * 濻瀂瀅瀆濸瀃瀂瀊濸瀅 + (4.70) * 濶瀈瀅濵-瀊濸濼濺濻瀇 + (81.96) * 濸瀁濺濼瀁濸-瀆濼瀍濸 + (33.58) * 濻濼濺濻瀊濴瀌-瀀瀃濺 如果回归的时候我们发现对应的模型不是线性模型怎么办?例如,像多项式 函数描述的非线性的模型该如何处理?假设 瀌 = β0 + β1 * 瀋 + β2 * 瀋^2 + β3 * 瀋^3,这时我们看到的,出现了高次(瀋 平方和 瀋 立方),说明这个模型就不是线性 模型。这时在数学上的处理是引入新的变量,将 瀋2 和 瀋3 引入,分别表示 瀋 平方 和 瀋 立方,把整个上面的公式就转换成了一个新的多元线性回归模型 瀌 = β0 + β1 * 瀋 + β2 * 瀋2 + β3 * 瀋3,通过这种方式来解决。 三、模型评估和可视化 我们是通过可视化来评估模型的。我们为什么要评估模型,原因是因为我们 想知道开发出来的模型能不能用做预测模型来预测未来的值。在评估的时候,我
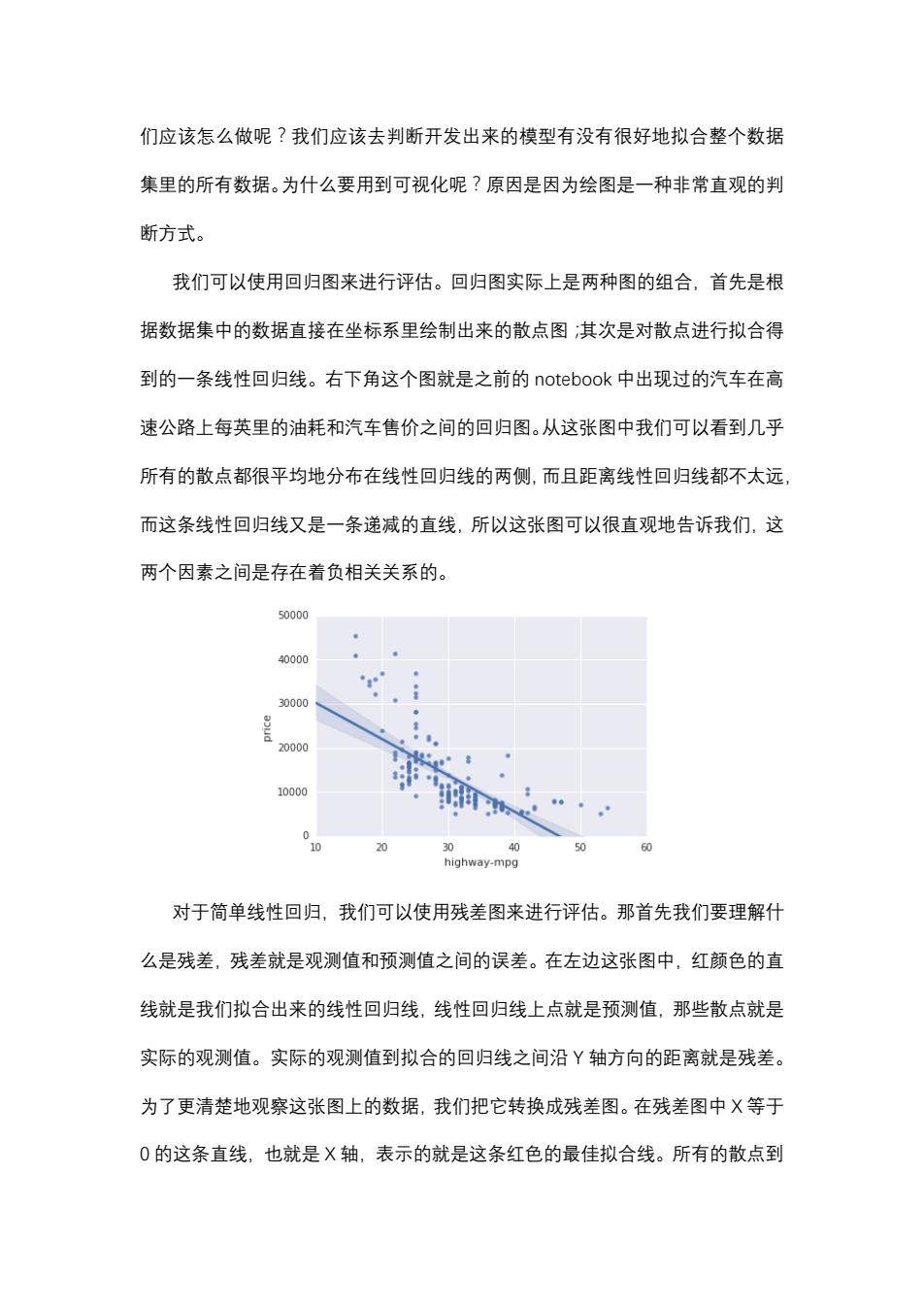
们应该怎么做呢?我们应该去判断开发出来的模型有没有很好地拟合整个数据 集里的所有数据。为什么要用到可视化呢?原因是因为绘图是一种非常直观的判 断方式。 我们可以使用回归图来进行评估。回归图实际上是两种图的组合,首先是根 据数据集中的数据直接在坐标系里绘制出来的散点图:其次是对散点进行拟合得 到的一条线性回归线。右下角这个图就是之前的notebook中出现过的汽车在高 速公路上每英里的油耗和汽车售价之间的回归图。从这张图中我们可以看到几乎 所有的散点都很平均地分布在线性回归线的两侧,而且距离线性回归线都不太远 而这条线性回归线又是一条递减的直线,所以这张图可以很直观地告诉我们,这 两个因素之间是存在着负相关关系的。 50000 40000 30000 20000 10000 0 20 0 40 50 60 highway-mpg 对于简单线性回归,我们可以使用残差图来进行评估。那首先我们要理解什 么是残差,残差就是观测值和预测值之间的误差。在左边这张图中,红颜色的直 线就是我们拟合出来的线性回归线,线性回归线上点就是预测值,那些散点就是 实际的观测值。实际的观测值到拟合的回归线之间沿Y轴方向的距离就是残差。 为了更清楚地观察这张图上的数据,我们把它转换成残差图。在残差图中X等于 0的这条直线,也就是X轴,表示的就是这条红色的最佳拟合线。所有的散点到
们应该怎么做呢?我们应该去判断开发出来的模型有没有很好地拟合整个数据 集里的所有数据。为什么要用到可视化呢?原因是因为绘图是一种非常直观的判 断方式。 我们可以使用回归图来进行评估。回归图实际上是两种图的组合,首先是根 据数据集中的数据直接在坐标系里绘制出来的散点图;其次是对散点进行拟合得 到的一条线性回归线。右下角这个图就是之前的 瀁瀂瀇濸濵瀂瀂濾 中出现过的汽车在高 速公路上每英里的油耗和汽车售价之间的回归图。从这张图中我们可以看到几乎 所有的散点都很平均地分布在线性回归线的两侧,而且距离线性回归线都不太远, 而这条线性回归线又是一条递减的直线,所以这张图可以很直观地告诉我们,这 两个因素之间是存在着负相关关系的。 对于简单线性回归,我们可以使用残差图来进行评估。那首先我们要理解什 么是残差,残差就是观测值和预测值之间的误差。在左边这张图中,红颜色的直 线就是我们拟合出来的线性回归线,线性回归线上点就是预测值,那些散点就是 实际的观测值。实际的观测值到拟合的回归线之间沿 Y 轴方向的距离就是残差。 为了更清楚地观察这张图上的数据,我们把它转换成残差图。在残差图中 X 等于 0 的这条直线,也就是 X 轴,表示的就是这条红色的最佳拟合线。所有的散点到