
五、协方差分析数学模型 y,=u+C,+B(x,-x)+ y-B(x,-x)=u+a+& y=ua+ 其中:B为x与y的总体直线回归系数
五、协方差分析数学模型 其中: 为x与y的总体直线回归系数 i j i j i i j i j i j i i j i j i i j y y ( x x ) y ( x x ) = + + − − = + + = + + − +

第二节单因素试验资料的协方差分析 设有k个处理、次重复的双变量试验资料 每处理组内皆有对观测值x、y,则该资料为 具kn对x、y观测值的单向分组资料,其数据 般模式如表10一1所示。 上一张下一张主页退出
第二节 单因素试验资料的协方差分析 设有k个处理、n次重复的双变量试验资料, 每处理组内皆有n对观测值x、y,则该资料为 具kn对x、y观测值的单向分组资料,其数据 一般模式如表10—1所示。 上一张 下一张 主 页 退 出
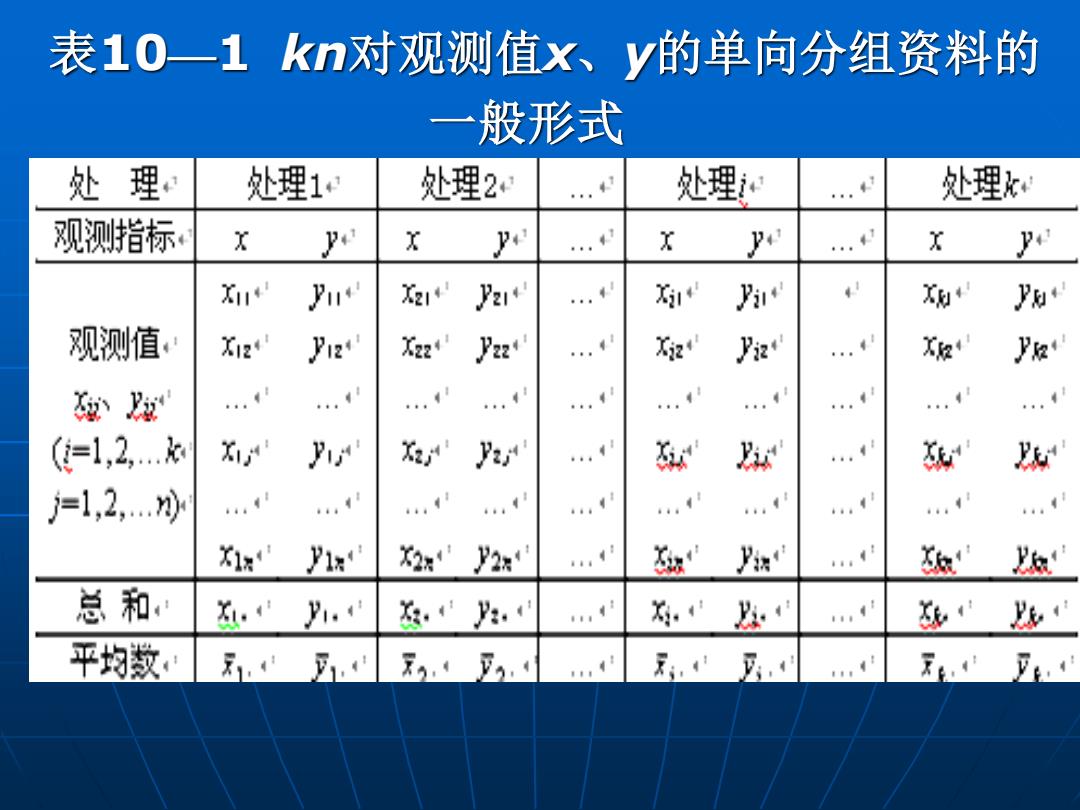
表10一1kn对观测值x、y的单向分组资料的 一般形式 处理 处理1 处理2 处理 处理k 观测指标 x P x P x P X y X214'y24 y乃 y阳 观测值 X12 y12 X22 乃2 Xiz Piz X取 ym a (=1,2… X 月 a =1,2,…炒 4 X1✉'1x X2✉'P2x 总和 .1,》 多 平均数. X2.42. 可
表10—1 kn对观测值x、y的单向分组资料的 一般形式

表10一1的x和y变量的自由度和平方和的剖分参 见单因素试验资料的方差分析方法一节。其乘积和的 剖分则为: 总变异的乘积和SP是x与x和y与.的离均 差乘积之和,即: SP=∑∑(x,-x)y,-) i=1j=1 ∑∑x, X..V.. (10-5) i=1j=1 kn =kn-1 上一张下一张主页退出
表10—1的x和y变量的自由度和平方和的剖分参 见单因素试验资料的方差分析方法一节。其乘积和的 剖分则为: 总变异的乘积和SPT是xji与 和yji与 的离均 差乘积之和,即: (10-5) =kn-1 x.. y.. k n x y x y SP x x y y k i n j i j i j k i n j T i j i j .. .. ( ..)( ..) 1 1 1 1 = − = − − = = = = T df 上一张 下一张 主 页 退 出

其中, x=∑x,y=之y i=1 i=1 x.=xkn ys-n
k n y y k n x x x x y y k i i k i i .. .. , .. .. .. ., .. ., 1 1 = = = = = = 其中