
3.1.1应力张量及其分解 72 平均正应力 m (11+02+)=30k (3-4) 应力张量可作如下分解: 13 033 一0m
平均正应力 = ( + + ) = (3 - 4) 3 1 3 1 m 1 1 2 2 3 3 k k 应力张量可作如下分解: 11 12 13 11 12 13 21 22 23 21 22 23 31 32 33 31 32 33 0 0 0 0 0 0 m m m m m m − = + − − 3.1.1 应力张量及其分解
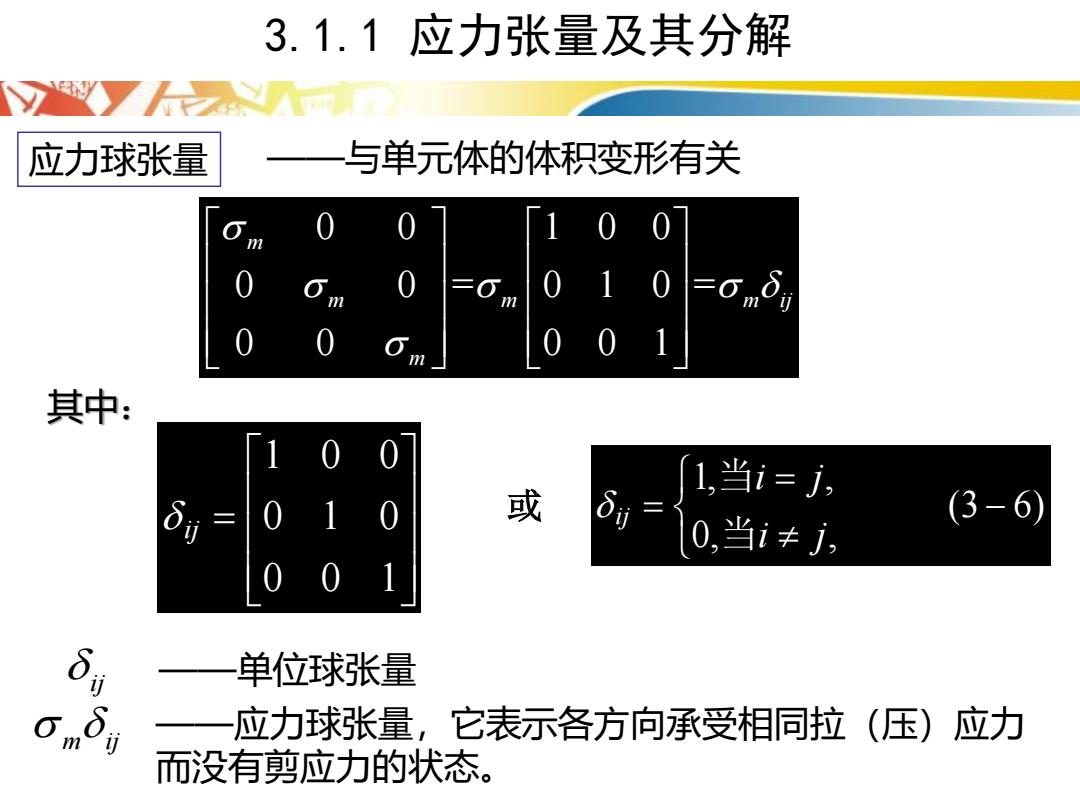
3.1.1应力张量及其分解 应力球张量 与单元体的体积变形有关 其中: 1,当i=j, 或 0,当i≠j。 (3-6) 单位球张量 应力球张量,它表示各方向承受相同拉(压)应力 m 而没有剪应力的状态
应力球张量 0 0 1 0 0 0 0 = 0 1 0 = 0 0 0 0 1 m m m m ij m ——与单元体的体积变形有关 其中: (3 6) 0, , 1, , − = = i j i j ij 当 当 = 0 0 1 0 1 0 1 0 0 ij 或 ij ——单位球张量 m ij ——应力球张量,它表示各方向承受相同拉(压)应力 而没有剪应力的状态。 3.1.1 应力张量及其分解
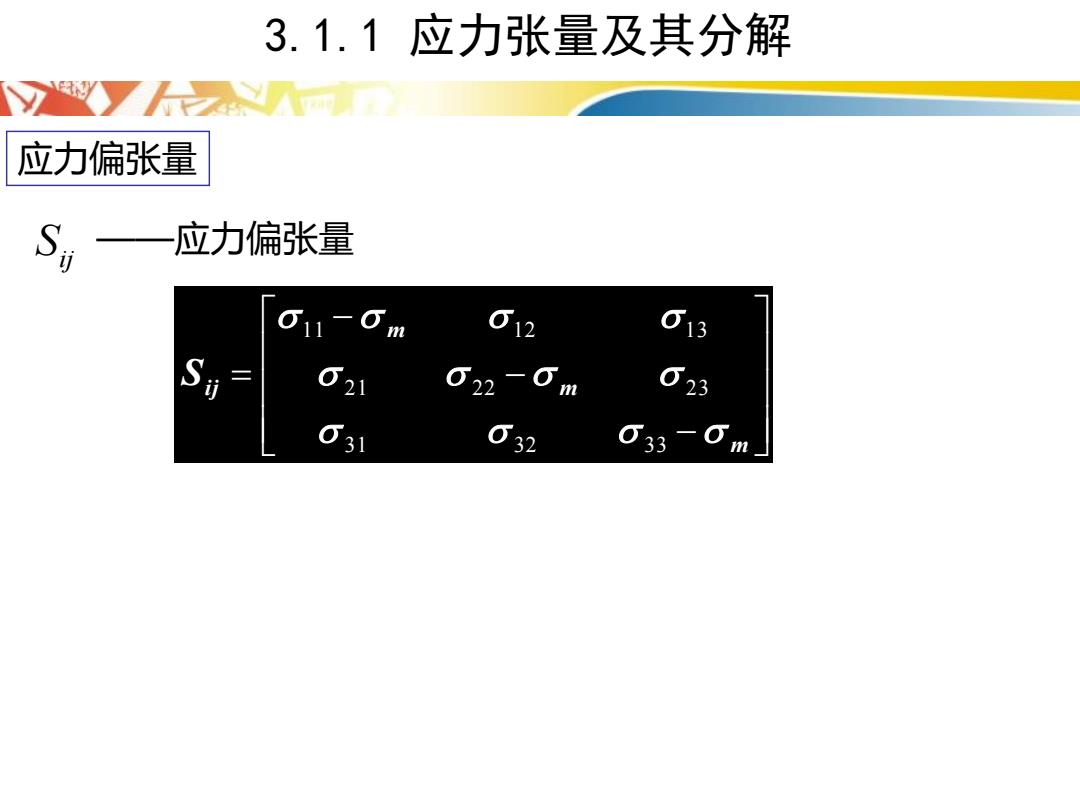
3.1.1应力张量及其分解 w了2m 应力偏张量 S,— 应力偏张量 012 12 3 032 033 -O
应力偏张量 ij S ——应力偏张量 − − − = m m m Si j 3 1 3 2 3 3 2 1 2 2 2 3 1 1 1 2 1 3 3.1.1 应力张量及其分解

3.1.1应力张量及其分解 应力张量分解: 用张量符号表示: =0m (3-5) 说明: 应力球张量 一与单元体的体积变形有关 应力偏张量 与单元体的形状改变有关 材料进入塑性后,单元体的体积变形是弹性的,只与应力球张量有 关;而与形状改变有关的塑性变形侧是由应力偏张量引起的
用张量符号表示: , (3 5) ij m ij ij = + − s 应力张量分解: 11 12 13 11 12 13 21 22 23 21 22 23 31 32 33 31 32 33 0 0 0 0 0 0 m m m m m m − = + − − 说明: 材料进入塑性后,单元体的体积变形是弹性的,只与应力球张量有 关;而与形状改变有关的塑性变形则是由应力偏张量引起的 。 应力球张量 应力偏张量 m ij ——与单元体的体积变形有关 ij S ——与单元体的形状改变有关 3.1.1 应力张量及其分解
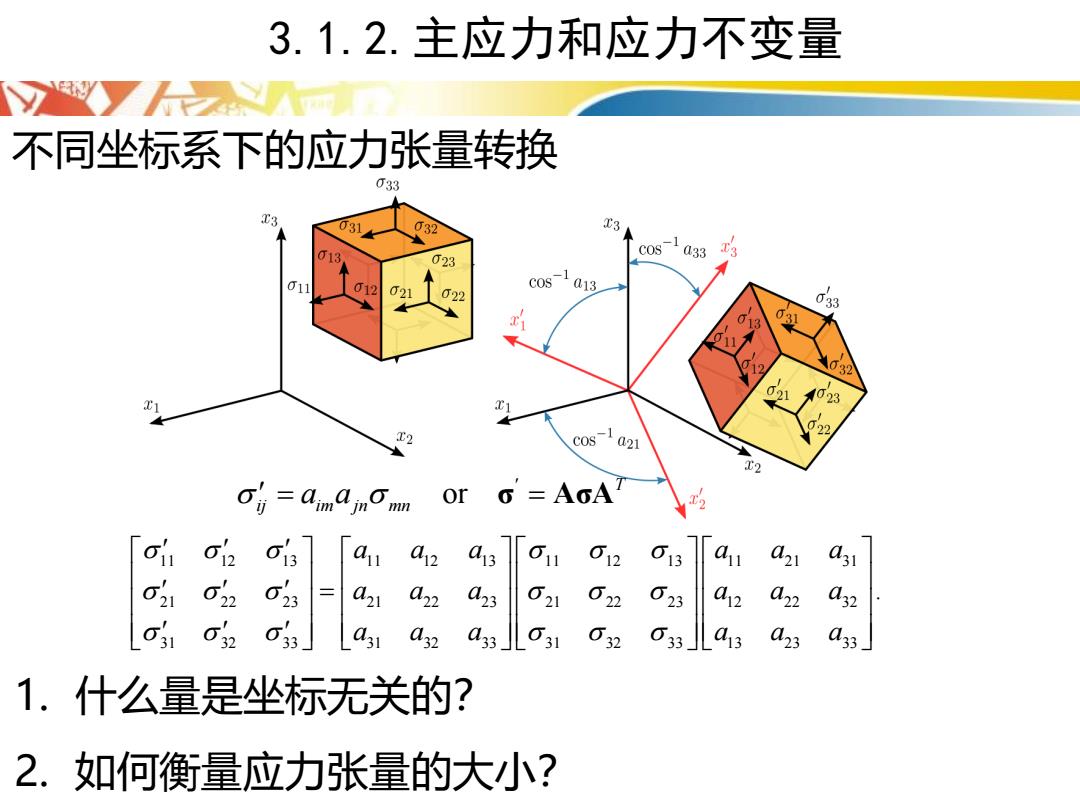
3.1.2.主应力和应力不变量 不同坐标系下的应力张量转换 033 032 713 023 cos-1a33 3 1 c0s-1a13 022 13 6 011 012 61 103 c0s-1a21 T2 or O=AcA a 3 02 3 av azi a31 0 6 a21 a22 03 61 62 623 a2 a22 a32 a31 a32 a33 031 032 033 a13 d23 1.什么量是坐标无关的? 2.如何衡量应力张量的大小?
3.1.2.主应力和应力不变量 11 12 13 11 12 13 11 12 13 11 21 31 21 22 23 21 22 23 21 22 23 12 22 32 31 32 33 31 32 33 31 32 33 13 23 33 . a a a a a a a a a a a a a a a a a a = or T ij im jn mn a a = = σ AσA 不同坐标系下的应力张量转换 1. 什么量是坐标无关的? 2. 如何衡量应力张量的大小?