
12.1.3放射性衰变系 在自然界出现的天然放射性核素,按其质量,可以划 分为Th、U和Ac三个系列。 其中Th、U和Ac是三个系列中半衰期最长的成员。它 们通过一系列的和B衰变,变成原子序数为82的铅的同位 素。 系与系间没有交错,即一个序列的核不能衰变为另一 序列的核。 Th4n系,包括13种核素,由232,Th0步衰变2082Pb; U4n十2)系,包括18种核素,由23,Ul4步衰变20“Pb: Ac4n十3)系,包括15种核素,由235,2U3步衰变27gAc 8步衰变207s2Pb。 括号中的数字表示一个特定系列的所有成员其质量数 都可以恰好被4整除,或者被4整除后的余数为2或3
12.1.3 放射性衰变系 在自然界出现的天然放射性核素,按其质量,可以划 分为Th、U和Ac三个系列。 其中Th、U和Ac是三个系列中半衰期最长的成员。它 们通过一系列的α和β衰变,变成原子序数为82的铅的同位 素。 系与系间没有交错,即一个序列的核不能衰变为另一 序列的核。 Th(4n)系,包括13种核素,由232 90Th 208 82Pb; U(4n+2)系,包括18种核素,由238 92U 206 82Pb; Ac(4n+3)系,包括15种核素,由235 92U 227 89Ac 207 82Pb。 括号中的数字表示一个特定系列的所有成员其质量数 都可以恰好被4整除,或者被4整除后的余数为2或3。 10步衰变 14步衰变 3步衰变 8步衰变

在发现了人造的铀后元素之后,又增添了镎系: Np(4n十1)系,包括15种核素,由24,4Pu2步衰变2372Np 11步衰变209s3Bi。 Np系与Th、U、Ac三系有明显的差别,它的最终产物 为20”s3Bi而不是82Pb。 系列的衰变步骤可根据系列的始末成员的质量和核电 荷及、B射线的知识所获得。例如,对Th系,假定放射了 a个a粒子和b个B粒子,则 质量变化数为232一208=4a,a=6; 核电荷变化为90一82=2a一b,b=4。 即2320Th经过6次α衰变和4次B衰变(共10步衰变)变为 2082Pb
系列的衰变步骤可根据系列的始末成员的质量和核电 荷及α、β射线的知识所获得。例如,对Th系,假定放射了 a个α粒子和b个β粒子,则 质量变化数为 232-208=4a,a=6; 核电荷变化为 90-82=2a-b,b=4。 即232 90Th经过6次α衰变和4次β衰变(共10步衰变)变为 208 82Pb。 在发现了人造的铀后元素之后,又增添了镎系: Np(4n+1)系,包括15种核素,由241 94Pu 237 92Np 209 83Bi。 Np系与Th、U、Ac三系有明显的差别,它的最终产物 为209 83Bi而不是82Pb。 11步衰变 2步衰变
h 6001460261108 221NP 217 213 209 U U 235 Ac 231 221Ac 223 219 206 215 表变核式 211 207 818283848586878889909192939495 TIPb Bi PoAt Rn Fr Ra Ac Th Pa U Np PuAm 四个放射性衰变系的衰变模式。其 中·是最稳定的核素,⊕是最终产物
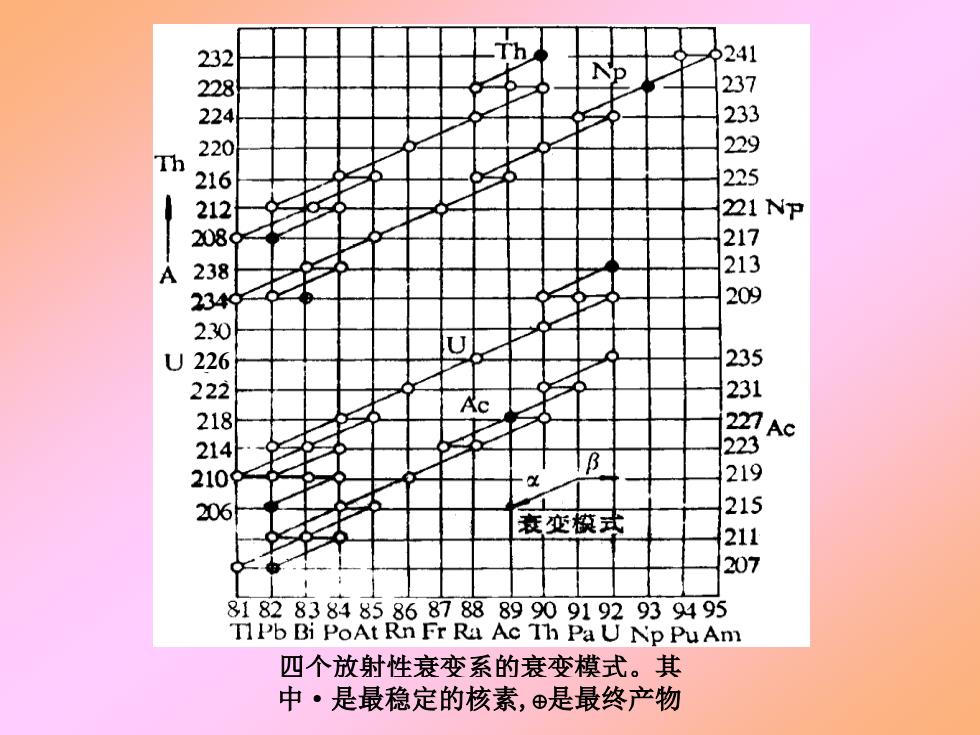
图 12.1 四个放射性衰变系的衰变模式。其 中·是最稳定的核素,是最终产物 图 12.1 四个放射性衰变系的衰变模式。其 中·是最稳定的核素,是最终产物 图 12.1 四个放射性衰变系的衰变模式。其 中·是最稳定的核素,是最终产物 226

12.2放射性衰变动力学 12.2.1衰变速率和半衰期 1放射性衰变定律 放射性衰变速率R(或放射性物质的放射活性A)正比于 放射核的数量N。由于R或A都是放射性核随时间t的变化 速率,所以 A=R=-dN/dtocN 或 A=R=-dN/dt=·N 式中为衰变常数,与核的本性有关,负号表明N随 时间的增加而减少,整理方程有 dNN=-·dt 1nN=-t+C 其中C为积分常数,当t=0,C=lnN,式中N为N的 初始值
12.2 放射性衰变动力学 12.2.1 衰变速率和半衰期 1 放射性衰变定律 放射性衰变速率R(或放射性物质的放射活性A)正比于 放射核的数量N。由于R或A都是放射性核随时间t的变化 速率,所以 A=R=-dN/dt∝N 或 A=R=-dN/dt=λ·N 式中λ为衰变常数,与核的本性有关,负号表明N随 时间的增加而减少,整理方程有 dN/N=-λ·dt 1nN=-λ·t+C 其中C为积分常数,当t=0,C=lnN0,式中N0为N的 初始值

经过变换,有 1nN-1nNo=-t 即 N-Noe-xt 或 t= 2.303 Ig N/N 这就是放射性衰变定律。 使用两套单位来计量衰变的速率: 居(里)C1,定义为一个放射源每秒发生3.700×1010 次衰变; 卢(瑟福)rd),定义为每秒衰变1×106次,显然, 1Ci=3.70X104rd
经过变换,有 1nN-1nN0 =-λ·t 即 N=N0 e-λt 或 t=- lg N/N0 这就是放射性衰变定律。 使用两套单位来计量衰变的速率: 居(里)(Ci),定义为一个放射源每秒发生3.700×1010 次衰变; 卢(瑟福)(rd),定义为每秒衰变1×106次,显然, 1 Ci=3.70×104 rd 2.303 λ