2.1关系模型的数据结构及其形式化定义 笛卡尔积可用二维表的形式表示: 姓 名 性 别 元组 李力 男 李力 女 王平 男 王平 女 刘伟 男 刘伟 女 同一域 笛卡尔积实际是一个二维表
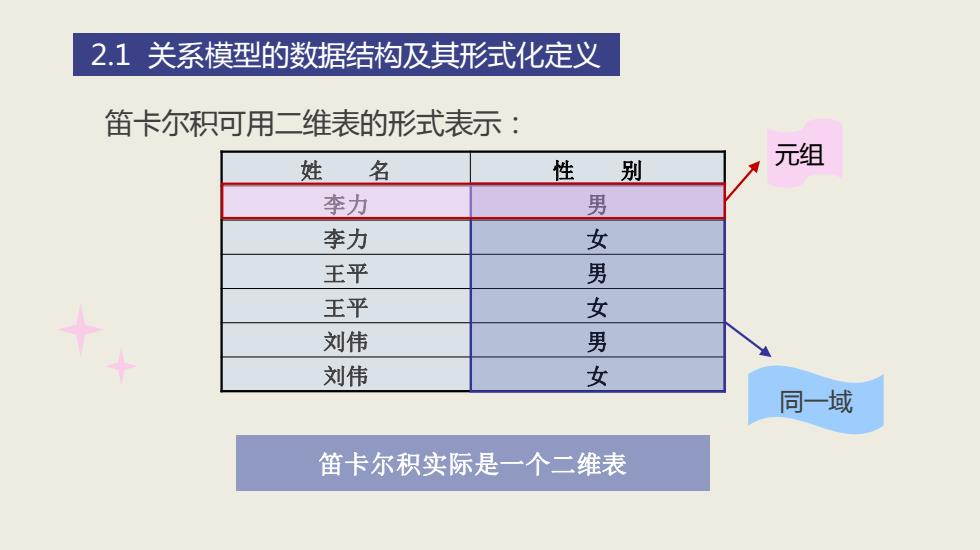
姓 名 性 别 李力 男 李力 女 王平 男 王平 女 刘伟 男 刘伟 女 笛卡尔积实际是一个二维表 元组 同一域 2.1 关系模型的数据结构及其形式化定义 笛卡尔积可用二维表的形式表示:

2.1关系模型的数据结构及其形式化定义 第2章 关系(Relation) 笛卡尔积D×D2×.×D的任一子集称为定义在域D,D2,·,Dn上的n元关系(Relation) 关系的名字 n是关系的目或度 R (D1,D2.,Dn) D1XD2笛卡尔积的子集(关系T1) 如,上例D1×D2笛卡尔积的某个子集 姓名 性 别 可以构成教师关系1,如表2.2所示 李力 男引 王平 女 刘伟 男
2.1 关系模型的数据结构及其形式化定义 第2章 R(D1,D2.,Dn) 笛卡尔积D1×D2×.×Dn的任一子集称为定义在域D1,D2,.,Dn上的n元关系(Relation) 关系的名字 n是关系的目或度 姓 名 性 别 李力 男 王平 女 刘伟 男 如,上例D1×D2笛卡尔积的某个子集 可以构成教师关系T1,如表2.2所示 D1×D2笛卡尔积的子集(关系T1) 关系(Relation)
2.1关系模型的数据结构及其形式化定义 第2章 在关系R中,当n=1时,称为单元关系。 当n=2时,称为二元关系,以此类推。 关系中的每个元素是关系中的元组,通常用表示, 关系中元组个数是关系的基数 由于关系是笛卡尔积的子集,因此, 也可以把关系看成一个二维表。 具有相同关系框架的关系称为同类关系。 属性 姓 名 性 别 元组 李力 男 属性的名字惟一 王平 女 刘伟 男 域
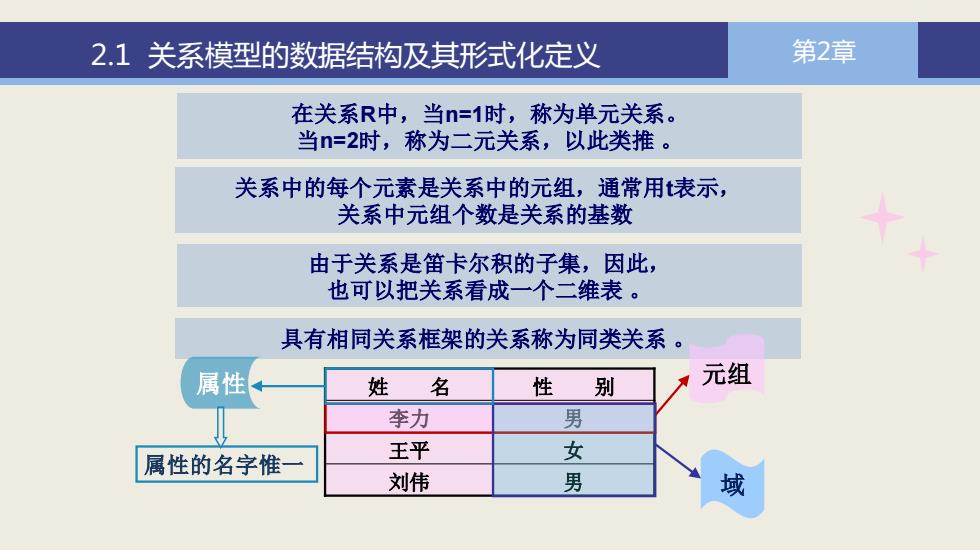
2.1 关系模型的数据结构及其形式化定义 第2章 在关系R中,当n=1时,称为单元关系。 当n=2时,称为二元关系,以此类推 。 关系中的每个元素是关系中的元组,通常用t表示, 关系中元组个数是关系的基数 由于关系是笛卡尔积的子集,因此, 也可以把关系看成一个二维表 。 具有相同关系框架的关系称为同类关系 。 姓 名 性 别 李力 男 王平 女 刘伟 男 元组 域 属性 属性的名字惟一
2.1关系模型的数据结构及其形式化定义 第2章 姓名 性别 李力 男 不符合实际意义的关系 李力 女 在关系模型中,关系可进一步定义为: 可变 不变 关系头(Heading)+关系体(Body) 由属性名的 关系结构中的 集合组成 内容或者数据
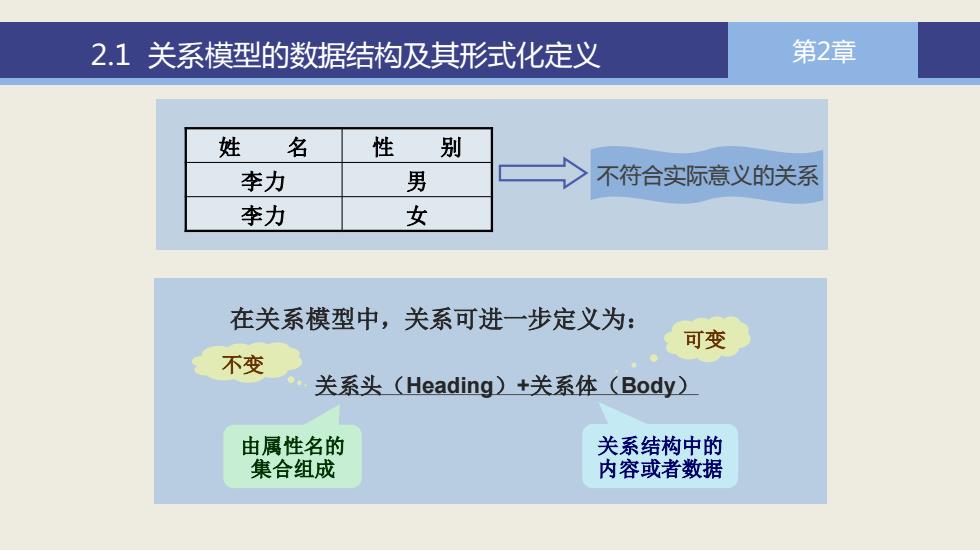
2.1 关系模型的数据结构及其形式化定义 第2章 姓 名 性 别 李力 男 李力 女 不符合实际意义的关系 由属性名的 集合组成 关系结构中的 内容或者数据 不变 可变 在关系模型中,关系可进一步定义为: 关系头(Heading)+关系体(Body)

2.1关系模型的数据结构及其形式化定义 第2章 2.1.2关系的性质 关系是一种规范化了的二维表中行的集合 每一列中的分量必须来自同一个域,必须是同一类型的数据。 ·不同的属性可来自同一个域,不同的属性必须有不同的名字。 ·列的顺序可以任意交换。 ·关系中元组的顺序(即行序)可任意。 ·关系中不允许出现相同的元组。 ·关系中每一分量必须是不可分的数据项
2.1 关系模型的数据结构及其形式化定义 第2章 2.1.2 关系的性质 关系是一种规范化了的二维表中行的集合 · 每一列中的分量必须来自同一个域,必须是同一类型的数据。 · 不同的属性可来自同一个域,不同的属性必须有不同的名字。 · 列的顺序可以任意交换。 · 关系中元组的顺序(即行序)可任意。 · 关系中不允许出现相同的元组。 · 关系中每一分量必须是不可分的数据项