上海交通大学：《大学物理》课程电子教案（PPT教学课件）静电场与物质的相互作用、电介质

**导体与静电场相互作用问题计算基本原则* √导体静电平衡的条件 导体内部 :0 √静电场基本方程 fE.ds=Σ9 ∮E.df-0 √电荷守恒定律 ∑g,=const

**导体与静电场相互作用问题计算基本原则** E 导体内部  0   qSE S 0 1 d      L lE 0d     i q i const. 导体静电平衡的条件 静电场基本方程 电荷守恒定律

[例题13-1两块近距离放置的导体平板，面积均为S,分别带 电q,和q2。求平板上的电荷分布。 解：电荷守恒： 01S+02S=94 91 2 03S+04S=92 由静电平衡条件，导体板内没有电场 E4 01020304 =0 28 2 26 260 04 B =0 280 280 260 28 01=04=9+9 2S 91-92 02=-03 2S

[例题13-1]两块近距离放置的导体平板，面积均为S，分别带 电q 1 和q2 。求平板上的电荷分布。 解： q1 q2 A B    qSS 121 由静电平衡条件，导体板内没有电场 0 2222 4321  oooo EA            41  2   3 0 2222 4321  ooOO EB         S qq 2  21  S qq 2  21  243    qSS 1 2 3 4 电荷守恒：

特例：当两平板带等量的相反电荷时， 91=-92=Q 01=04=0 41 42 02=-0 S 电荷只分布在两个平板的内表面！ 04 由此可知：两平板外侧电场强度为零， 内侧 E= A B Eo —这就是平板电容器。 01=04= 9+92 2S 02=-03= 91-92 2S END

END 特例：当两平板带等量的相反电荷时，   21  Qqq    41  2   3  0   S Q 电荷只分布在两个平板的内表面！ 由此可知：两平板外侧电场强度为零， 内侧 0   E  ——这就是平板电容器。 q1 q2 A B    41  2   3 S qq 2  21  S qq 2  21  1 2 3 4

§13.1.2.2导体空腔 本节讨论如图所示有空腔的导 体与静电场的相互作用问题。 9 包括： (1)导体空腔上的电荷分布特征 (2)空间电场分布特征

§13.1.2.2 13.1.2.2 导体空腔 包括： （1）导体空腔上的电荷分布特征 （2）空间电场分布特征 本节讨论如图所示有空腔的导 体与静电场的相互作用问题。 . q

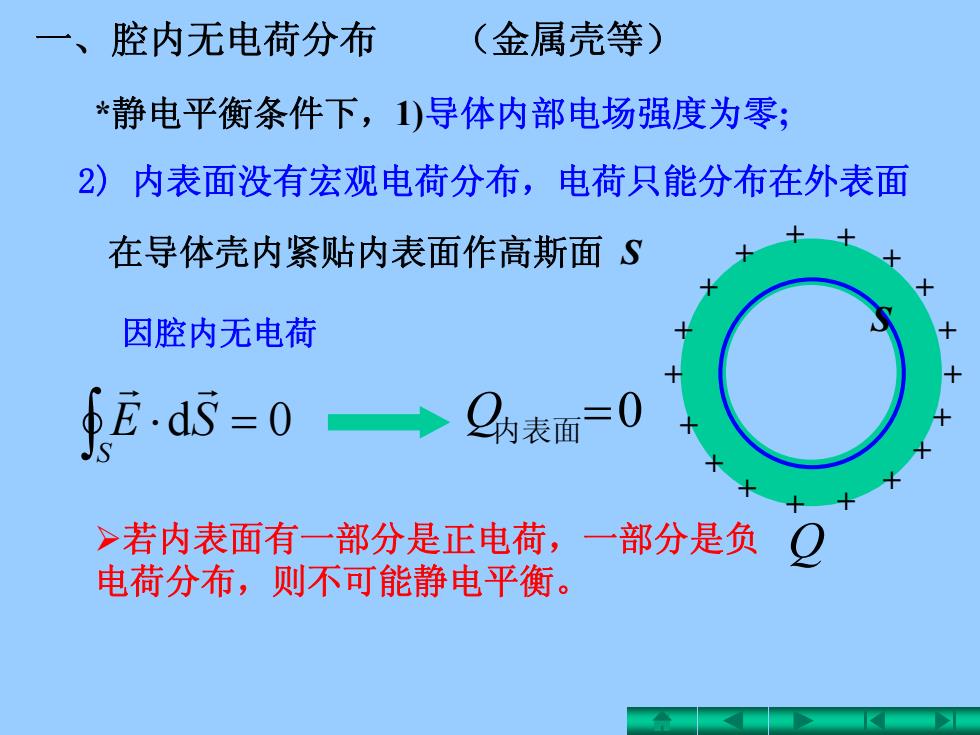
一、腔内无电荷分布 (金属壳等) *静电平衡条件下，1)导体内部电场强度为零； 2)内表面没有宏观电荷分布，电荷只能分布在外表面 在导体壳内紧贴内表面作高斯面S 因腔内无电荷 fE.dS=0→Q表面=0 >若内表面有一部分是正电荷，一部分是负Q 电荷分布，则不可能静电平衡

S  0d S SE  一、腔内无电荷分布 （金属壳等） 2) 内表面没有宏观电荷分布，电荷只能分布在外表面 在导体壳内紧贴内表面作高斯面 S Q内表面0 若内表面有一部分是正电荷，一部分是负 电荷分布，则不可能静电平衡。 *静电平衡条件下，1)导体内部电场强度为零; + + + + + + + + + + + + + + + + + + Q 因腔内无电荷