大连理工大学：《数据结构》课程教学课件（PPT讲稿）第六章 图

①② ③ ④ ⑤ 例 5 ①「0 7 0 3 3 8 ② 0 0 4 8 4 ③7 0 0 2 1 6 3 ④ 0 4 20 6 2 ⑤3 8 16 0」

 3 8 1 6 0 0 4 2 0 6 7 0 0 2 1 5 0 0 4 8 0 5 7 0 3       例 1 4 5 2 3 7 5 3 1 8 6 4 2

★关联矩阵一 表示顶点与边的关联关系的矩阵 定义：设G=(N,E)是有≥1个顶点，e≥0条边的图，G的关联矩 阵A是具有以下性质的nxe阶矩阵 1,顶点与边相连，且为尾 有向图：A[i,门=0，顶点与边不相连 -1,顶点与边相连，且为头 1,顶点与边相连 无向图：4i,刀= 0,顶点与边不相连

关联矩阵——表示顶点与边的关联关系的矩阵 ❖定义：设G=(V,E)是有n1个顶点，e0条边的图，G的关联矩 阵A是具有以下性质的ne阶矩阵      − = 顶点与 边相连，且 为头 顶点与 边不相连 顶点与 边相连，且 为尾 有向图： i j i i j i j i A i j 1, 0, 1, [ , ]    = ， 顶点与 边不相连 ， 顶点与 边相连 无向图： i j i j A i j 0 1 [ , ]

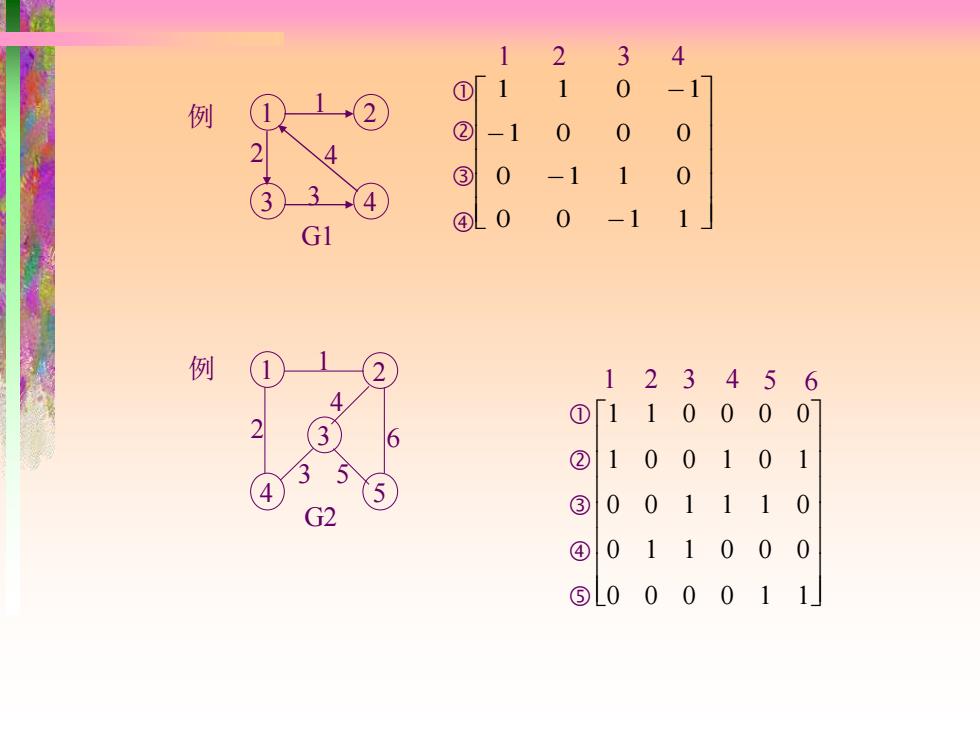
1 2 3 4 ①「1 1 0 -1 例 ② -1 0 0 0 0 -1 1 0 3 -11 G1 L00 例 2 123456 ①「110 00 07 6 ②10 0101 G2 ③001110 ④01 1000 ⑤L000 011

  − − − − 0 0 1 1 0 1 1 0 1 0 0 0  1 1 0 1  1 2 3 4 例 G1 24 13 1 2 3 4 例 1 5 3 2 4 G21 2 3 45 6   0 0 0 0 1 1 0 1 1 0 0 0 0 0 1 1 1 0 1 0 0 1 0 1 1 1 0 0 0 0 1 2 3 4 5 6

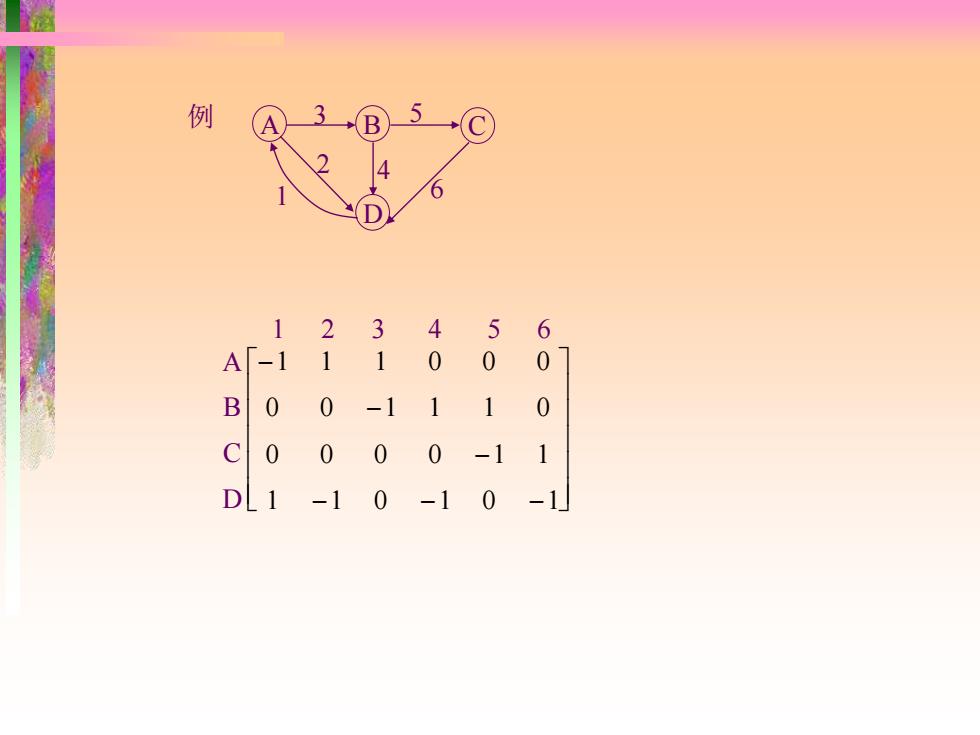
例 A 1 2 3 4 5 6 A「-1 1 1 0 0 0 B 0 0 -1 1 1 0 C 0 0 0 0 -1 1 -1 0 -1 0 -1

例 B D A C 1 2 3 4 5 6 A B C D 1 2 3 4 5 6               − − − − − − 1 1 0 1 0 1 0 0 0 0 1 1 0 0 1 1 1 0 1 1 1 0 0 0

特点 ●关联矩阵每列只有两个非零元素，是稀疏矩阵；越大，零 元素比率越大 ●无向图中顶点V的度TD个V)是关联矩阵A中第行元素之和 ●有向图中， ◆顶点V的出度是A中第i行中“1”的个数 ◆顶点V的入度是A中第行中“-1”的个数

❖特点 ⚫关联矩阵每列只有两个非零元素，是稀疏矩阵；n越大，零 元素比率越大 ⚫无向图中顶点Vi的度TD(Vi)是关联矩阵A中第i行元素之和 ⚫有向图中， ◆顶点Vi的出度是A中第i行中“1”的个数 ◆顶点Vi的入度是A中第i行中“-1”的个数