路径:1,2,3,5,6,3 例 路径长度:5 简单路径:1,2,3,5 ▣路:1,2,3,5,6,3,1 3 6 简单回路:3,5,6,3 G1 例 5 7 路径:1,2,5,7,6,5,2,3 路径长度:7 简单路径:1,2,5,7,6 4 6 回路:1,2,5,7,6,5,2,1 G2 简单回路:1,2,3,1
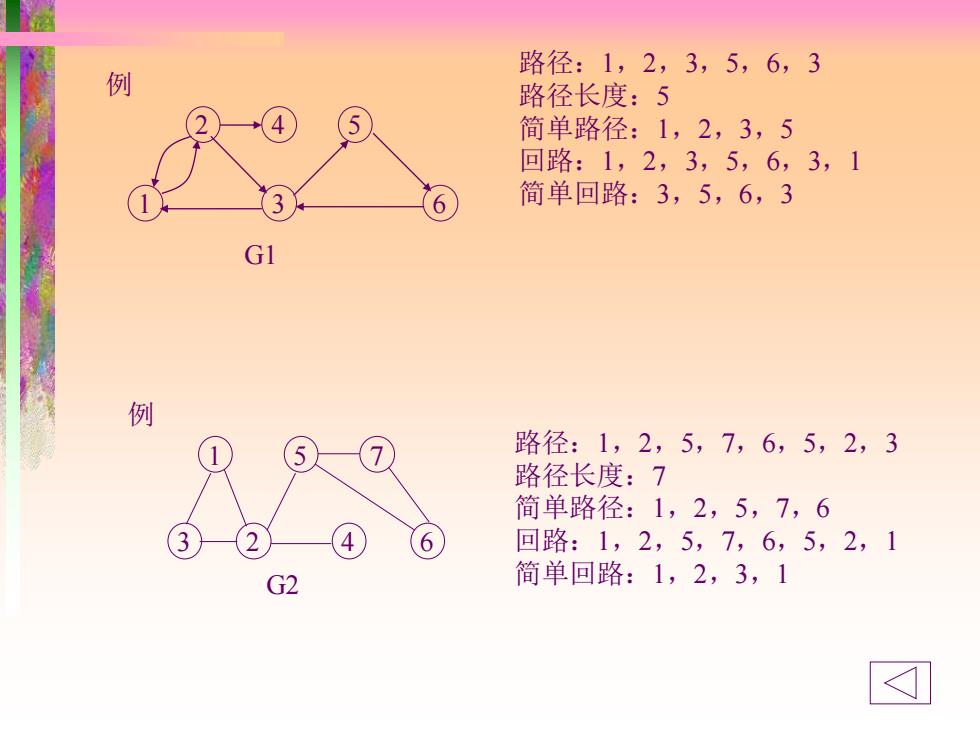
例 1 5 7 3 2 4 G2 6 例 2 4 5 1 3 6 G1 路径:1,2,3,5,6,3 路径长度:5 简单路径:1,2,3,5 回路:1,2,3,5,6,3,1 简单回路:3,5,6,3 路径:1,2,5,7,6,5,2,3 路径长度:7 简单路径:1,2,5,7,6 回路:1,2,5,7,6,5,2,1 简单回路:1,2,3,1
例 4 5 连通图 3 6 例 5 强连通图 6 例 5 非连通图 连通分量 3 6
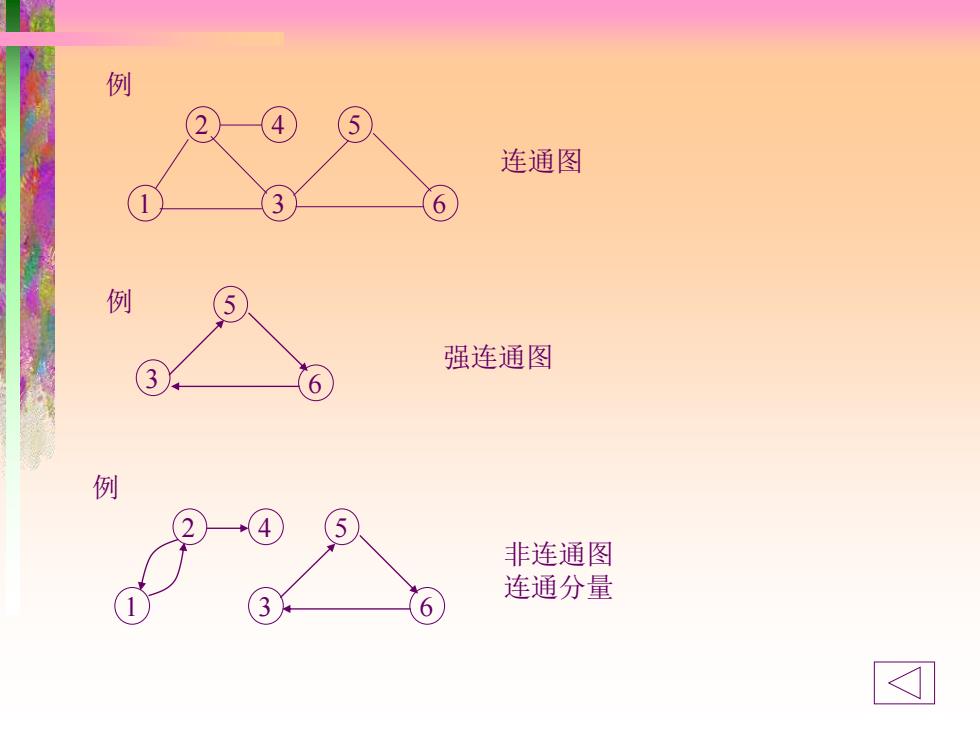
连通图 例 2 4 5 1 3 6 强连通图 3 5 6 例 非连通图 连通分量 例 2 4 5 1 3 6
§6.2图的存储结构 ★多重链表 例 V4☑ V2 3 4 V3 G1 例 2 G2 Vs
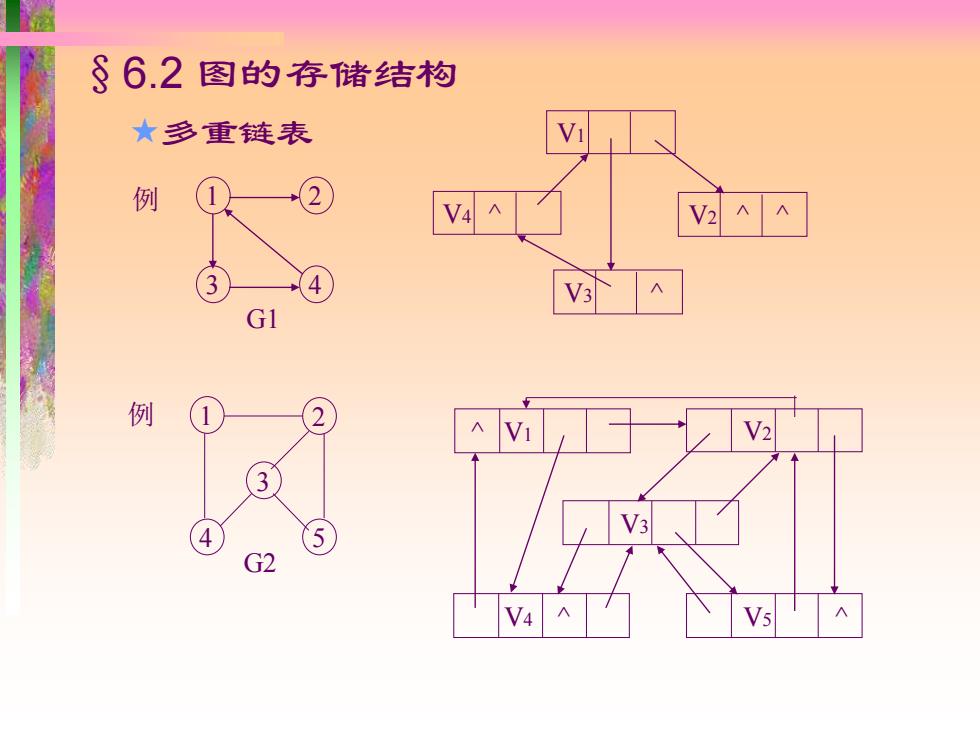
§6.2 图的存储结构 多重链表 例 G1 2 4 1 3 例 1 5 3 2 4 G2 V1 V4 ^ V2 ^ ^ V3 ^ ^ V1 V2 V4 ^ V5 ^ V3

★邻接矩阵一表示顶点间相联关系的矩阵 定义:设G=(N,E)是有≥1个顶点的图,G的邻接矩阵A是具有 以下性质的n阶方阵 1,若(N,V)减<V,V,>∈E(G) A,]= 0,其它 ①②③ ④ ①「0 11 0 例 2 ② 0 0 0 0 ③ 0 0 01 ④L1 00 0 GI ①②③④ ⑤ 例 2 ①「01 01 0 ②10 1 01 ③ 0 1 011 5 ④101 0 0 G2 ⑤011 0 0
邻接矩阵——表示顶点间相联关系的矩阵 ❖定义:设G=(V,E)是有n1个顶点的图,G的邻接矩阵A是具有 以下性质的n阶方阵 = 0,其它 1,若(v , v )或 v , v E(G) [ , ] i j i j A i j 例 G1 2 4 1 3 例 1 5 3 2 4 G2 0 1 1 0 0 1 0 1 0 0 0 1 0 1 1 1 0 1 0 1 0 1 0 1 0 1 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0

冬特点: ●无向图的邻接矩阵对称,可压缩存储;有个顶点的无向图 需存储空间为n(n+1)/2 ●有向图邻接矩阵不一定对称;有个顶点的有向图需存储空 间为n2 ●无向图中顶点V的度TDV)是邻接矩阵A中第i行元素之和 ●有向图中, ◆顶点V的出度是A中第行元素之和 ◆顶点V的入度是A中第列元素之和 ●网络的邻接矩阵可定义为: 0,若(V,V)或<V,V,>∈E(G) A[i,刀= 0,其它
❖特点: ⚫无向图的邻接矩阵对称,可压缩存储;有n个顶点的无向图 需存储空间为n(n+1)/2 ⚫有向图邻接矩阵不一定对称;有n个顶点的有向图需存储空 间为n² ⚫无向图中顶点Vi的度TD(Vi)是邻接矩阵A中第i行元素之和 ⚫有向图中, ◆顶点Vi的出度是A中第i行元素之和 ◆顶点Vi的入度是A中第i列元素之和 ⚫网络的邻接矩阵可定义为: = 0,其它 ,若(v , v )或 v , v E(G) [ , ] i j i j i j A i j