
第8卷第5期 智能系统学报 VoL.8 No.5 2013年10月 CAAI Transactions on Intelligent Systems 0ct.2013 D0:10.3969/j.issn.1673-4785.201110007 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.TP.20130929.1049.003.html 线性插值框架下矩阵步态识别的性能分析 贲晛烨,张鹏,潘婷婷,王科俊 (1.山东大学信息科学与工程学院,山东济南250100:2.哈尔滨工程大学自动化学院,黑龙江哈尔滨150001) 摘要:针对现有的步态周期检测方法检测效果不佳以及行走速度变化对步态识别性能有很大影响的问题,提出的 基于矩的步态周期检测方法中,Zernike矩需要人体居中、尺度归一的前期预处理过程,而伪Zernike矩具有能描述运 动图像的特点,它可以避免人体居中、尺度归一等处理,以便直接测试步态的周期性.根据行走时的两帧之间的特征 取决于前一帧和后一帧的特征,提出了基于线性插值的矩阵步态识别算法框架,并且将投影特征、Hough变换特征、 Trace变换特征和Fan-Beam映射特征应用在CASIA(B)步态库上,验证了框架的有效性,为解决步态识别问题带来 新的方法与思路这种基于线性插值的矩阵步态识别特征本质上是一种权值不同的能量形式. 关键词:步态识别:矩阵步态识别:线性插值框架;步态周期检测;Zernike矩;伪Zernike矩 中图分类号:TP391.41文献标志码:A文章编号:1673-4785(2013)05-0415-11 中文引用格式:贲晛烨,张鹏,潘婷婷,等.线性插值框架下矩阵步态识别的性能分析[J】.智能系统学报,2013,8(5):415425. 英文引用格式:BEN Xianye,ZHANG Peng,PAN Tingting,etal.Performance analysis of matrix gait recognition under linear in- terpolation framework[J].CAAI Transactions on Intelligent Systems,2013,8(5):415-425. Performance analysis of matrix gait recognition under linear interpolation framework BEN Xianye',ZHANG Peng',PAN Tingting',WANG Kejun2 (1.School of Information Science and Engineering,Shandong University,Ji'nan 250100,China;2.College of Automation,Harbin Engineering University,Harbin 150001,China) Abstract:The existing gait period detection methods are not ideal and the performance of gait recognition is signifi- cantly influenced by walking speed.Several novel gait period detection methods based on moments are proposed in this paper.The Zernike moment requires preprocessing including the assurance that the image of the human body is proportioned normally and is centered properly;the pseudo-Zernike moment may directly describe the motion im- age,and it may avoid the need for such processing of making the image of the human body centered and sized nor- mally,so as to directly detect gait periodicity.As the features of one frame are only decided by those of the prior and the rear frames in walking,a framework for a matrix gait recognition algorithm based on linear interpolation is proposed.Subsequently,the projection features,Hough transform feature,Trace transform feature and Fan-Beam mapping feature are applied to the CASIA(B)gait database to prove the validity of the gait recognition framework. This brings new methods and understanding for solving gait recognition problems.This matrix gait recognition feature based on linear interpolation is essentially an energy form with different weighted values. Keywords:gait recognition;matrix gait recognition;linear interpolation framework;gait period detection;Zernike moment;pseudo-Zernike moment 步态识别是在人没有觉察的远距离情况下,通 特征具有稳定性、普遍性、可采集性和惟一性,因此 过捕捉动态与静态信息来进行身份识别.由于步态 可用于不同场合下的身份识别与认证).Nixon等] 收稿日期:2011-10-19.网络出版日期:2013-09-29 总结了南安普敦大学2002年之前研发的步态识别 基金项目:国家自然科学基金资助项目(61201370):高等学校博士学 技术,同时预言了步态应用于生物特征识别的潜能, 科点专项科研基金资助项目(20120131120030):中国博土 后科学基金面上项目(2013M530321):山东省博土后创新 2005年,Boulgouris等I)首先将步态识别与其他生 项目专项资金项目(201303100):山东大学自主创新基金 物特征识别做了比较,提出步态识别可以作为多生 资助项目(2012GN043,2012DX007). 通信作者:贲現烨.E-mail:benxianyeye@l63.com 物特征识别技术的一部分,接着给出了步态识别系
第 8 卷第 5 期 智 能 系 统 学 报 Vol.8 №.5 2013 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2013 DOI:10.3969 / j.issn.1673 ̄4785.201110007 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20130929.1049.003.html 线性插值框架下矩阵步态识别的性能分析 贲晛烨1 ꎬ张鹏1 ꎬ潘婷婷1 ꎬ王科俊2 (1.山东大学 信息科学与工程学院ꎬ山东 济南 250100ꎻ 2.哈尔滨工程大学 自动化学院ꎬ黑龙江 哈尔滨 150001) 摘 要:针对现有的步态周期检测方法检测效果不佳以及行走速度变化对步态识别性能有很大影响的问题ꎬ提出的 基于矩的步态周期检测方法中ꎬZernike 矩需要人体居中、尺度归一的前期预处理过程ꎬ而伪 Zernike 矩具有能描述运 动图像的特点ꎬ它可以避免人体居中、尺度归一等处理ꎬ以便直接测试步态的周期性.根据行走时的两帧之间的特征 取决于前一帧和后一帧的特征ꎬ提出了基于线性插值的矩阵步态识别算法框架ꎬ并且将投影特征、Hough 变换特征、 Trace 变换特征和 Fan ̄Beam 映射特征应用在 CASIA(B)步态库上ꎬ验证了框架的有效性ꎬ为解决步态识别问题带来 新的方法与思路.这种基于线性插值的矩阵步态识别特征本质上是一种权值不同的能量形式. 关键词:步态识别ꎻ矩阵步态识别ꎻ线性插值框架ꎻ步态周期检测ꎻZernike 矩ꎻ伪 Zernike 矩 中图分类号:TP391.41 文献标志码:A 文章编号:1673 ̄4785(2013)05 ̄0415 ̄11 中文引用格式:贲晛烨ꎬ张鹏ꎬ潘婷婷ꎬ等.线性插值框架下矩阵步态识别的性能分析[J]. 智能系统学报ꎬ 2013ꎬ 8(5): 415 ̄425. 英文引用格式:BEN Xianyeꎬ ZHANG Pengꎬ PAN Tingtingꎬ et al. Performance analysis of matrix gait recognition under linear in ̄ terpolation framework[J]. CAAI Transactions on Intelligent Systemsꎬ 2013ꎬ 8(5): 415 ̄425. Performance analysis of matrix gait recognition under linear interpolation framework BEN Xianye 1 ꎬ ZHANG Peng 1 ꎬ PAN Tingting 1 ꎬ WANG Kejun 2 (1. School of Information Science and Engineeringꎬ Shandong Universityꎬ Ji’ nan 250100ꎬ Chinaꎻ 2. College of Automationꎬ Harbin Engineering Universityꎬ Harbin 150001ꎬ China) Abstract:The existing gait period detection methods are not ideal and the performance of gait recognition is signifi ̄ cantly influenced by walking speed. Several novel gait period detection methods based on moments are proposed in this paper. The Zernike moment requires preprocessing including the assurance that the image of the human body is proportioned normally and is centered properlyꎻ the pseudo ̄Zernike moment may directly describe the motion im ̄ ageꎬ and it may avoid the need for such processing of making the image of the human body centered and sized nor ̄ mallyꎬ so as to directly detect gait periodicity. As the features of one frame are only decided by those of the prior and the rear frames in walkingꎬ a framework for a matrix gait recognition algorithm based on linear interpolation is proposed. Subsequentlyꎬ the projection featuresꎬ Hough transform featureꎬ Trace transform feature and Fan ̄Beam mapping feature are applied to the CASIA(B) gait database to prove the validity of the gait recognition framework. This brings new methods and understanding for solving gait recognition problems. This matrix gait recognition feature based on linear interpolation is essentially an energy form with different weighted values. Keywords:gait recognitionꎻ matrix gait recognitionꎻ linear interpolation frameworkꎻ gait period detectionꎻ Zernike momentꎻ pseudo ̄Zernike moment 收稿日期:2011 ̄10 ̄19. 网络出版日期:2013 ̄09 ̄29. 基金项目:国家自然科学基金资助项目(61201370)ꎻ高等学校博士学 科点专项科研基金资助项目(20120131120030)ꎻ中国博士 后科学基金面上项目(2013M530321)ꎻ山东省博士后创新 项目专项资金项目( 201303100)ꎻ山东大学自主创新基金 资助项目(2012GN043ꎬ2012DX007). 通信作者:贲晛烨. E ̄mail: benxianyeye@ 163.com. 步态识别是在人没有觉察的远距离情况下ꎬ通 过捕捉动态与静态信息来进行身份识别.由于步态 特征具有稳定性、普遍性、可采集性和惟一性ꎬ因此 可用于不同场合下的身份识别与认证[1] .Nixon 等[2] 总结了南安普敦大学 2002 年之前研发的步态识别 技术ꎬ同时预言了步态应用于生物特征识别的潜能. 2005 年ꎬBoulgouris 等[3] 首先将步态识别与其他生 物特征识别做了比较ꎬ提出步态识别可以作为多生 物特征识别技术的一部分ꎬ接着给出了步态识别系

416 智能系统学报 第8卷 统在其中的组成结构,最后给出了步态识别中隐马 右大腿、左腿肚和右腿肚6个部分,然后对每一部 尔可夫模型的统计方法、步态周期检测、基于模型的 分采用椭圆来拟合,最后采用椭圆参数的欧式距 方法、外观方法、时间序列的频域变换、降维方法、模 离或马氏距离进行身份识别.鉴于时间归一化存 板匹配方法.2012年,贲現烨等从人体测量学数 在较为复杂的调整过程,而关键帧所含的信息量 据、空间时间数据、运动学数据、动力学数据和视频 不足,本文提出基于Zernike矩(或者伪Zernike 流数据方面总结了步态识别的各种方法.在视频流 矩)的步态周期检测算法,并在一个完整的步态周 数据的计算机视觉的各种方法中,行人行走速度的 期内采用线性插值框架下的矩阵步态识别方法, 变化会影响步态识别的性能,样本的采样只能选取 最后分析和总结识别性能, 部分速率,因此样本间的匹配呈动态特性.就此, 1 Boulgouris等提出2种时间归一化方法,即动态时间 步态周期检测 规整(dynamic time warping,DTW))和线性时间归 首先提取视频中单帧图像进行灰度变换,选择 一(linear time normalization,LTN)[6.田光见等f]和 不含人体的图像作为原始背景图像,然后通过实时 Hog等[8)都是采用DTW进行步态匹配,而且都是 更新的背景减除法提取人体目标,根据Kapur嫡阈 在时间域上进行.DTW和LTN可捕捉步态的时空特 值法对图像序列进行二值化处理,利用数学形态学 性,但是计算较为复杂,而且特征数据较多.Nandini 方法填充二值化图像的空洞,通过单连通分析提取 等)提出关键帧对行走速度变化而言是鲁棒的,是 人的轮廓,将人体轮廓放置在图像中间,图像的大小 最大信息的压缩索引.BenAbdelkader等[o]采用关键 统一归一到64×64大小),最后检测被分割出的人 帧的自相似图(self-similarity plot,SSP)作为步态的 体,去除包含不完整人体的冗余帧),图1所示为 特征于仕琪等)使用关键帧的傅里叶描述子来表 视频图像处理的结果.之后再逐帧计算Zernike矩 达步态特征,该方法不需要周期对齐.徐俊红等[] (或伪Zernike矩),作为分隔步态周期的依据,即起 将关键帧的步态分成头部、躯干和下肢(膝关节以 始帧为第1次出现局部极值,终止帧为第3次出现 上和膝关节以下)4个部分或者头、躯干、左大腿、 局部极值的前一帧。 图1步态图像预处理的结果 Fig.1 Results of gait images preprocessing l.l基于Zernike矩的步态周期检测 力强.在Zernike矩中,阶次较低的代表了图像的低 Zernike矩就是图像函数f(x,y)在正交基函 频特征,阶次较高的代表了图像的高频特征,因此, 数Vm(P,9)上的投影.在单位圆外趋于零的连续图 用其提取的特征还可以反映一定的动态特性.测试 像函数的n阶m重Zernike矩为 如图1所示的步态序列,采用前面所述的图像序列 2n=+1 ∬fx,y)Va(p,)dxdy.(1) 预处理方法,逐帧计算Zernike矩Zo的模数,测试 下2+3261 结果如图2所示.由于Zernike矩定义的特征只具有 对于一个数字图像,积分被求和代替,式(1)就 旋转不变性,为了获取尺度和平移不变量,步态序列 变为 图像还需要标准化处理, 名=”告Σ,.0+≤1 ×10 为了计算给定图像的Zernike矩,把图像的中心 作为原点,其他点的坐标被映射到单位圆内,即x2+ y2≤1,落在单位圆外的那些点不参与计算, 10 2030 40 50 60 Zernike矩具有以下优点:1)旋转不变性;2)信 帧数 息表达的冗余性小,所提取特征的相关性和冗余性 (a)未经人体居中、大小归一等步骤 小:3)容易构造高阶不变矩:4)鲁棒性好,抗噪声能
统在其中的组成结构ꎬ最后给出了步态识别中隐马 尔可夫模型的统计方法、步态周期检测、基于模型的 方法、外观方法、时间序列的频域变换、降维方法、模 板匹配方法.2012 年ꎬ贲晛烨等[4] 从人体测量学数 据、空间时间数据、运动学数据、动力学数据和视频 流数据方面总结了步态识别的各种方法.在视频流 数据的计算机视觉的各种方法中ꎬ行人行走速度的 变化会影响步态识别的性能ꎬ样本的采样只能选取 部分速率ꎬ因此样本间的匹配呈动态特性. 就此ꎬ Boulgouris 等提出 2 种时间归一化方法ꎬ即动态时间 规整(dynamic time warpingꎬ DTW) [5]和线性时间归 一(linear time normalizationꎬ LTN) [6] .田光见等[7]和 Hong 等[8]都是采用 DTW 进行步态匹配ꎬ而且都是 在时间域上进行.DTW 和 LTN 可捕捉步态的时空特 性ꎬ但是计算较为复杂ꎬ而且特征数据较多.Nandini 等[9]提出关键帧对行走速度变化而言是鲁棒的ꎬ是 最大信息的压缩索引.BenAbdelkader 等[10]采用关键 帧的自相似图(self ̄similarity plotꎬ SSP)作为步态的 特征.于仕琪等[11]使用关键帧的傅里叶描述子来表 达步态特征ꎬ该方法不需要周期对齐.徐俊红等[12] 将关键帧的步态分成头部、躯干和下肢(膝关节以 上和膝关节以下)4 个部分或者头、躯干、左大腿、 右大腿、左腿肚和右腿肚 6 个部分ꎬ然后对每一部 分采用椭圆来拟合ꎬ最后采用椭圆参数的欧式距 离或马氏距离进行身份识别.鉴于时间归一化存 在较为复杂的调整过程ꎬ而关键帧所含的信息量 不足ꎬ 本 文 提 出 基 于 Zernike 矩 ( 或 者 伪 Zernike 矩)的步态周期检测算法ꎬ并在一个完整的步态周 期内采用线性插值框架下的矩阵步态识别方法ꎬ 最后分析和总结识别性能. 1 步态周期检测 首先提取视频中单帧图像进行灰度变换ꎬ选择 不含人体的图像作为原始背景图像ꎬ然后通过实时 更新的背景减除法提取人体目标ꎬ根据 Kapur 熵阈 值法对图像序列进行二值化处理ꎬ利用数学形态学 方法填充二值化图像的空洞ꎬ通过单连通分析提取 人的轮廓ꎬ将人体轮廓放置在图像中间ꎬ图像的大小 统一归一到 64×64 大小[1] ꎬ最后检测被分割出的人 体ꎬ去除包含不完整人体的冗余帧[13] ꎬ图 1 所示为 视频图像处理的结果.之后再逐帧计算 Zernike 矩 (或伪 Zernike 矩)ꎬ作为分隔步态周期的依据ꎬ即起 始帧为第 1 次出现局部极值ꎬ终止帧为第 3 次出现 局部极值的前一帧. 图 1 步态图像预处理的结果 Fig.1 Results of gait images preprocessing 1.1 基于 Zernike 矩的步态周期检测 Zernike 矩[14]就是图像函数 f(xꎬy) 在正交基函 数 V ∗ nm(ρꎬθ) 上的投影.在单位圆外趋于零的连续图 像函数的 n 阶 m 重 Zernike 矩为 Znm = n + 1 π ∬ x 2+y 2≤1 f(xꎬy)V ∗ nm(ρꎬθ)dxdy . (1) 对于一个数字图像ꎬ积分被求和代替ꎬ式(1)就 变为 Znm = n + 1 π ∑x ∑y f(xꎬy)V ∗ nm(ρꎬθ)ꎬx 2 + y 2 ≤ 1. 为了计算给定图像的 Zernike 矩ꎬ把图像的中心 作为原点ꎬ其他点的坐标被映射到单位圆内ꎬ即 x 2 + y 2 ≤ 1ꎬ 落在单位圆外的那些点不参与计算. Zernike 矩具有以下优点:1)旋转不变性ꎻ2)信 息表达的冗余性小ꎬ所提取特征的相关性和冗余性 小ꎻ3)容易构造高阶不变矩ꎻ4)鲁棒性好ꎬ抗噪声能 力强.在 Zernike 矩中ꎬ阶次较低的代表了图像的低 频特征ꎬ阶次较高的代表了图像的高频特征ꎬ因此ꎬ 用其提取的特征还可以反映一定的动态特性.测试 如图 1 所示的步态序列ꎬ采用前面所述的图像序列 预处理方法ꎬ逐帧计算 Zernike 矩 Z20 的模数ꎬ测试 结果如图 2 所示.由于 Zernike 矩定义的特征只具有 旋转不变性ꎬ为了获取尺度和平移不变量ꎬ步态序列 图像还需要标准化处理. (a)未经人体居中、大小归一等步骤 416 智 能 系 统 学 报 第 8 卷

第5期 贲硯烨,等:线性插值框架下矩阵步态识别的性能分析 ·417- ×10 10 10 10203040 5060 帧数 10 2030 40 5060 帧数 (b)经人体居中、大小归一等步骤 图2使用Z如的模数的检测效果 (a)未经人体居中、大小归一等步骤 Fig.2 Detection results using the modulus of Zernike moment Z2o ×10 10 1.2基于伪Zernike矩的步态周期检测 伪Zernike矩[s]的离散化公式为 20 3040 5060 帧数 三三R_pep(-jm,Nx,以 (b)经人体居中、大小归一等步骤 图3使用Z。的模数的检测效果 式中:p=√x2+y2表示极距,0表示极角,fx, Fig.3 Detection results using the modulus of pseudo- Zernike moment Zo y)(-1≤x≤1,-1≤y≤1)表示以坐标原点为 圆心的单位圆的灰度图像, ×103 2.5 Rm(p)= 2.0 n-1ml (2n+1-s)! (a!(-m!(m1! 1.0 0.5 p-6±VB-4c 10 2030 4050 60 2a 帧数 伪Zernike矩的优点如下:l)旋转不变性;2)鲁 棒性好,即对形状的微小改变和噪声具有鲁棒性,同 图4使用Z的模数的检测效果 Zernike矩相比,在相同阶的情况下,伪Zernike矩具 Fig.4 Detection results using the modulus of pseudo- Zernike moment Z 有更多的低阶矩,低阶矩越多,抗噪声的能力就越 强,例如当阶为5时,伪Zernike矩有21个矩,而 2 线性插值的矩阵步态识别算法框架 Zernike矩只有12个矩;3)信息表达的冗余性小:4) 信息表达的高效性,一幅图像可以用很少的伪 根据人行走时2帧之间的特征决定于前一帧和 后一帧的特征,采用牛顿线性插值法将离散的步态 Zernike矩集合很好地表示,且具有较小的均方误 序列模拟成近似连续步态,为实现识别阶段快速的 差;5)多层次表达,相关的一组伪Zernike矩的小集 匹配,通过构造特征模板将一个周期的步态序列图 合就可以有效地表示一个模式的全部形状,其中低 像表征为矩阵.牛顿线性插值法可表达成两点式,即 阶矩描述的是一个模式的整体形状,而高阶矩描述 的是模式的细节:6)能描述运动图像,可用于运动 g(x)=f(xo)- +)二和 0-x1 x1-x0 图像序列分析. 式中:(xof(xo)与(x1f(x1)表示直线上的2 仍然测试如图1所示的步态序列,采用前述图 个点 像序列预处理方法,逐帧计算伪Zernike矩Z。的模 令f。表示第n幅步态单帧图像,F。是此图像对 数,测试结果如图3所示.利用伪Zernike矩的优点 应的特征,即t时刻恰好对应第n幅步态图像: 6),在前述预处理的标准中心化之前逐帧计算伪 F(t)=F,t=n. 通过牛顿线性插值构造出第n帧和第n+1帧 Zernike矩Z的模数,测试结果如图4所示. 之间的特征为
(b)经人体居中、大小归一等步骤 图 2 使用 Z20 的模数的检测效果 Fig. 2 Detection results using the modulus of Zernike moment Z20 1.2 基于伪 Zernike 矩的步态周期检测 伪 Zernike 矩[ 15 ]的离散化公式为 Z p nm = n + 1 π ∑ 1 x = -1∑ 1 y = -1 Rnm(ρ)exp( - jmθxy)f(xꎬy). 式中: ρ = x 2 + y 2 表示极距ꎬ θxy 表示极角ꎬ f(xꎬ y)( - 1 ≤ x ≤ 1ꎬ - 1 ≤ y ≤ 1) 表示以坐标原点为 圆心的单位圆的灰度图像ꎬ Rnm(ρ) = ∑ n-| m | s = 0 (( - 1) s (2n + 1 - s)! s! (n - m - s)! (n + m + 1 - s)! × ρ n-s - b ± b 2 - 4ac 2a ). 伪 Zernike 矩的优点如下:1)旋转不变性ꎻ2)鲁 棒性好ꎬ即对形状的微小改变和噪声具有鲁棒性ꎬ同 Zernike 矩相比ꎬ在相同阶的情况下ꎬ伪 Zernike 矩具 有更多的低阶矩ꎬ低阶矩越多ꎬ抗噪声的能力就越 强ꎬ例如当阶为 5 时ꎬ伪 Zernike 矩有 21 个矩ꎬ而 Zernike 矩只有 12 个矩ꎻ3)信息表达的冗余性小ꎻ4) 信息表 达 的 高 效 性ꎬ 一 幅 图 像 可 以 用 很 少 的 伪 Zernike 矩集合很好地表示ꎬ且具有较小的均方误 差ꎻ5)多层次表达ꎬ相关的一组伪 Zernike 矩的小集 合就可以有效地表示一个模式的全部形状ꎬ其中低 阶矩描述的是一个模式的整体形状ꎬ而高阶矩描述 的是模式的细节ꎻ6) 能描述运动图像ꎬ可用于运动 图像序列分析. 仍然测试如图 1 所示的步态序列ꎬ采用前述图 像序列预处理方法ꎬ逐帧计算伪 Zernike 矩 Z p 10 的模 数ꎬ测试结果如图 3 所示.利用伪 Zernike 矩的优点 6)ꎬ在前述预处理的标准中心化之前逐帧计算伪 Zernike 矩 Z p 53 的模数ꎬ测试结果如图 4 所示. (a)未经人体居中、大小归一等步骤 (b)经人体居中、大小归一等步骤 图 3 使用 Z p 10 的模数的检测效果 Fig.3 Detection results using the modulus of pseudo ̄ Zernike moment Z p 10 图 4 使用 Z p 53 的模数的检测效果 Fig.4 Detection results using the modulus of pseudo ̄ Zernike moment Z p 53 2 线性插值的矩阵步态识别算法框架 根据人行走时 2 帧之间的特征决定于前一帧和 后一帧的特征ꎬ采用牛顿线性插值法将离散的步态 序列模拟成近似连续步态ꎬ为实现识别阶段快速的 匹配ꎬ通过构造特征模板将一个周期的步态序列图 像表征为矩阵.牛顿线性插值法可表达成两点式ꎬ即 g(x) = f(x0 ) x - x1 x0 - x1 + f(x1 ) x - x0 x1 - x0 . 式中: (x0 ꎬf(x0 )) 与 (x1 ꎬf(x1 )) 表示直线上的 2 个点. 令 f n 表示第 n 幅步态单帧图像ꎬ Fn 是此图像对 应的特征ꎬ即 t 时刻恰好对应第 n 幅步态图像: F(t) = Fn ꎬ t = n. 通过牛顿线性插值构造出第 n 帧和第 n+1 帧 之间的特征为 第 5 期 贲晛烨ꎬ等:线性插值框架下矩阵步态识别的性能分析 417
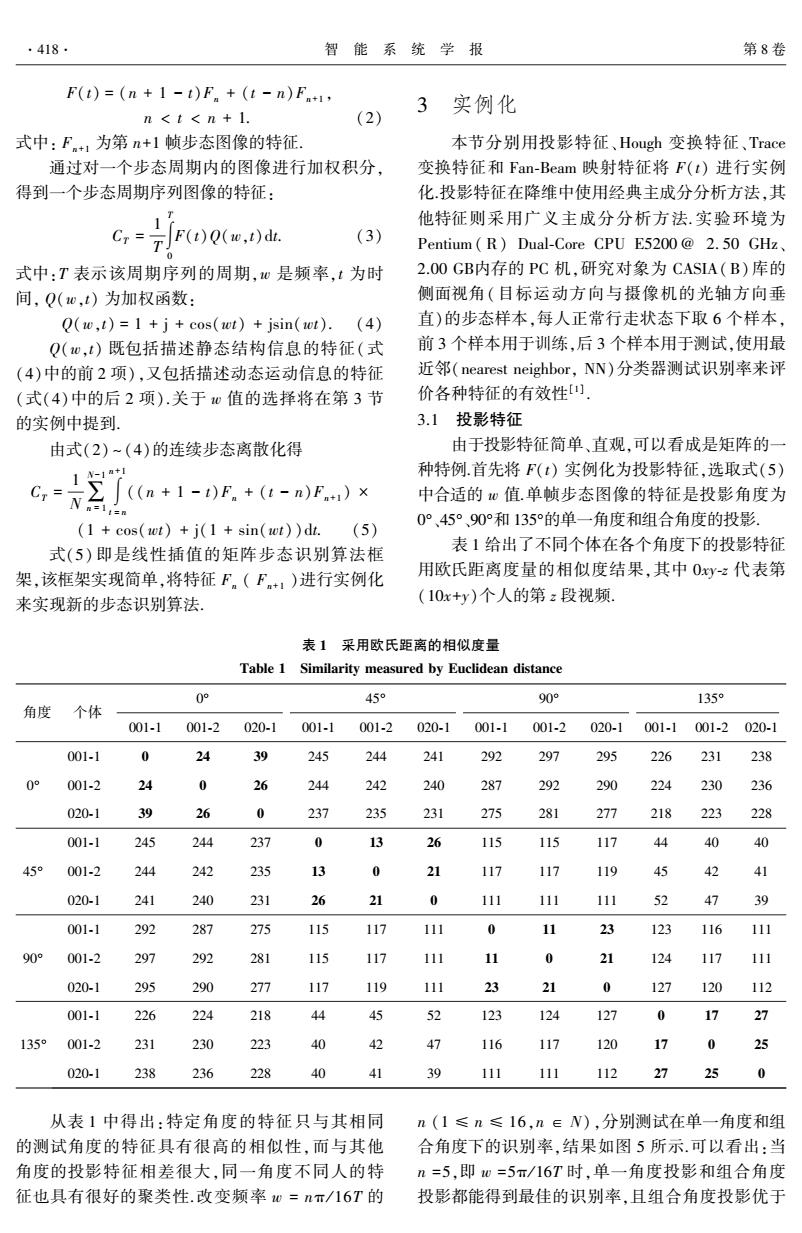
.418 智能系统学报 第8卷 F(t)=(n+1-t)F.+(t-n)Fa1, 3 实例化 n<t<n+1. (2) 式中:F+1为第n+1帧步态图像的特征 本节分别用投影特征、Hough变换特征、Trace 通过对一个步态周期内的图像进行加权积分, 变换特征和Fan-Beam映射特征将F(t)进行实例 得到一个步态周期序列图像的特征: 化.投影特征在降维中使用经典主成分分析方法,其 他特征则采用广义主成分分析方法.实验环境为 G,=7F()0(o,)d (3) Pentium(R)Dual-Core CPU E5200@2.50GHz、 式中:T表示该周期序列的周期,心是频率,t为时 2.O0GB内存的PC机,研究对象为CASIA(B)库的 间,Q(w,t)为加权函数: 侧面视角(目标运动方向与摄像机的光轴方向垂 Q(w,t)=1 +j+cos(wt)+jsin(wt).(4) 直)的步态样本,每人正常行走状态下取6个样本, Q(0,t)既包括描述静态结构信息的特征(式 前3个样本用于训练,后3个样本用于测试,使用最 (4)中的前2项),又包括描述动态运动信息的特征 近邻(nearest neighbor,NN)分类器测试识别率来评 (式(4)中的后2项).关于心值的选择将在第3节 价各种特征的有效性[). 的实例中提到. 3.1投影特征 由式(2)~(4)的连续步态离散化得 由于投影特征简单、直观,可以看成是矩阵的一 1 A-1n+I 种特例.首先将F(t)实例化为投影特征,选取式(5) 之J(n+1-)F.+(t-n)F)× Cr= 中合适的心值.单帧步态图像的特征是投影角度为 (1 cos(wt)+j(1 sin(wt))dt.(5) 0°、45°、90°和135°的单一角度和组合角度的投影. 式(5)即是线性插值的矩阵步态识别算法框 表1给出了不同个体在各个角度下的投影特征 架,该框架实现简单,将特征F。(F+1)进行实例化 用欧氏距离度量的相似度结果,其中0xy-z代表第 来实现新的步态识别算法, (10x+y)个人的第z段视频。 表1采用欧氏距离的相似度量 Table 1 Similarity measured by Euclidean distance 0° 45 90° 135 角度 个体 001-1 001-2 020-1 001-1 001-2 020-1 001-1 001-2 020-1 001-1 001-2 020-1 001-1 24 39 245 244 241 292 297 295 226 231 238 0° 001-2 24 0 26 244 242 240 287 292 290 224 230 236 020-1 39 26 235 231 275 281 277 218 223 228 001-1 245 244 237 26 115 115 117 44 40 40 45° 001-2 244 242 235 117 117 119 45 42 41 020-1 241 240 2 52 47 39 001-1 292 287 275 115 23 123 116 111 90° 001-2 297 292 28 11 117 11 21 124 117 111 020-1 295 290 2 127 120 112 001-1 226 224 218 45 52 123 124 127 17 27 1359 001-2 231 230 223 40 42 47 116 117 120 17 0 25 020-1 238 236 228 40 41 39 111 111 112 27 25 0 从表1中得出:特定角度的特征只与其相同 n(1≤n≤16,n∈N),分别测试在单一角度和组 的测试角度的特征具有很高的相似性,而与其他 合角度下的识别率,结果如图5所示.可以看出:当 角度的投影特征相差很大,同一角度不同人的特 n=5,即0=5π/16T时,单一角度投影和组合角度 征也具有很好的聚类性.改变频率o=nπ/16T的 投影都能得到最佳的识别率,且组合角度投影优于
F(t) = (n + 1 - t)Fn + (t - n)Fn+1 ꎬ n < t < n + 1. (2) 式中: Fn+1 为第 n+1 帧步态图像的特征. 通过对一个步态周期内的图像进行加权积分ꎬ 得到一个步态周期序列图像的特征: CT = 1 T ∫ T 0 F(t)Q(wꎬt)dt. (3) 式中:T 表示该周期序列的周期ꎬw 是频率ꎬt 为时 间ꎬ Q(wꎬt) 为加权函数: Q(wꎬt) = 1 + j + cos(wt) + jsin(wt). (4) Q(wꎬt) 既包括描述静态结构信息的特征(式 (4)中的前 2 项)ꎬ又包括描述动态运动信息的特征 (式(4)中的后 2 项).关于 w 值的选择将在第 3 节 的实例中提到. 由式(2) ~ (4)的连续步态离散化得 CT = 1 N∑ N-1 n = 1 ∫ n+1 t = n ((n + 1 - t)Fn + (t - n)Fn+1 ) × (1 + cos(wt) + j(1 + sin(wt))dt. (5) 式(5) 即是线性插值的矩阵步态识别算法框 架ꎬ该框架实现简单ꎬ将特征 Fn ( Fn+1 )进行实例化 来实现新的步态识别算法. 3 实例化 本节分别用投影特征、Hough 变换特征、Trace 变换特征和 Fan ̄Beam 映射特征将 F(t) 进行实例 化.投影特征在降维中使用经典主成分分析方法ꎬ其 他特征则采用广义主成分分析方法. 实验环境为 Pentium ( R) Dual ̄Core CPU E5200 @ 2. 50 GHz、 2.00 GB内存的 PC 机ꎬ研究对象为 CASIA(B)库的 侧面视角(目标运动方向与摄像机的光轴方向垂 直)的步态样本ꎬ每人正常行走状态下取 6 个样本ꎬ 前 3 个样本用于训练ꎬ后 3 个样本用于测试ꎬ使用最 近邻(nearest neighborꎬ NN)分类器测试识别率来评 价各种特征的有效性[1] . 3.1 投影特征 由于投影特征简单、直观ꎬ可以看成是矩阵的一 种特例.首先将 F(t) 实例化为投影特征ꎬ选取式(5) 中合适的 w 值.单帧步态图像的特征是投影角度为 0°、45°、90°和 135°的单一角度和组合角度的投影. 表 1 给出了不同个体在各个角度下的投影特征 用欧氏距离度量的相似度结果ꎬ其中 0xy ̄z 代表第 (10x+y)个人的第 z 段视频. 表 1 采用欧氏距离的相似度量 Table 1 Similarity measured by Euclidean distance 角度 个体 0° 001 ̄1 001 ̄2 020 ̄1 45° 001 ̄1 001 ̄2 020 ̄1 90° 001 ̄1 001 ̄2 020 ̄1 135° 001 ̄1 001 ̄2 020 ̄1 0° 001 ̄1 0 24 39 245 244 241 292 297 295 226 231 238 001 ̄2 24 0 26 244 242 240 287 292 290 224 230 236 020 ̄1 39 26 0 237 235 231 275 281 277 218 223 228 45° 001 ̄1 245 244 237 0 13 26 115 115 117 44 40 40 001 ̄2 244 242 235 13 0 21 117 117 119 45 42 41 020 ̄1 241 240 231 26 21 0 111 111 111 52 47 39 90° 001 ̄1 292 287 275 115 117 111 0 11 23 123 116 111 001 ̄2 297 292 281 115 117 111 11 0 21 124 117 111 020 ̄1 295 290 277 117 119 111 23 21 0 127 120 112 135° 001 ̄1 226 224 218 44 45 52 123 124 127 0 17 27 001 ̄2 231 230 223 40 42 47 116 117 120 17 0 25 020 ̄1 238 236 228 40 41 39 111 111 112 27 25 0 从表 1 中得出:特定角度的特征只与其相同 的测试角度的特征具有很高的相似性ꎬ而与其他 角度的投影特征相差很大ꎬ同一角度不同人的特 征也具有很好的聚类性.改变频率 w = nπ / 16T 的 n (1 ≤ n ≤ 16ꎬn ∈ N) ꎬ分别测试在单一角度和组 合角度下的识别率ꎬ结果如图 5 所示.可以看出:当 n =5ꎬ即 w =5π/ 16T 时ꎬ单一角度投影和组合角度 投影都能得到最佳的识别率ꎬ且组合角度投影优于 418 智 能 系 统 学 报 第 8 卷
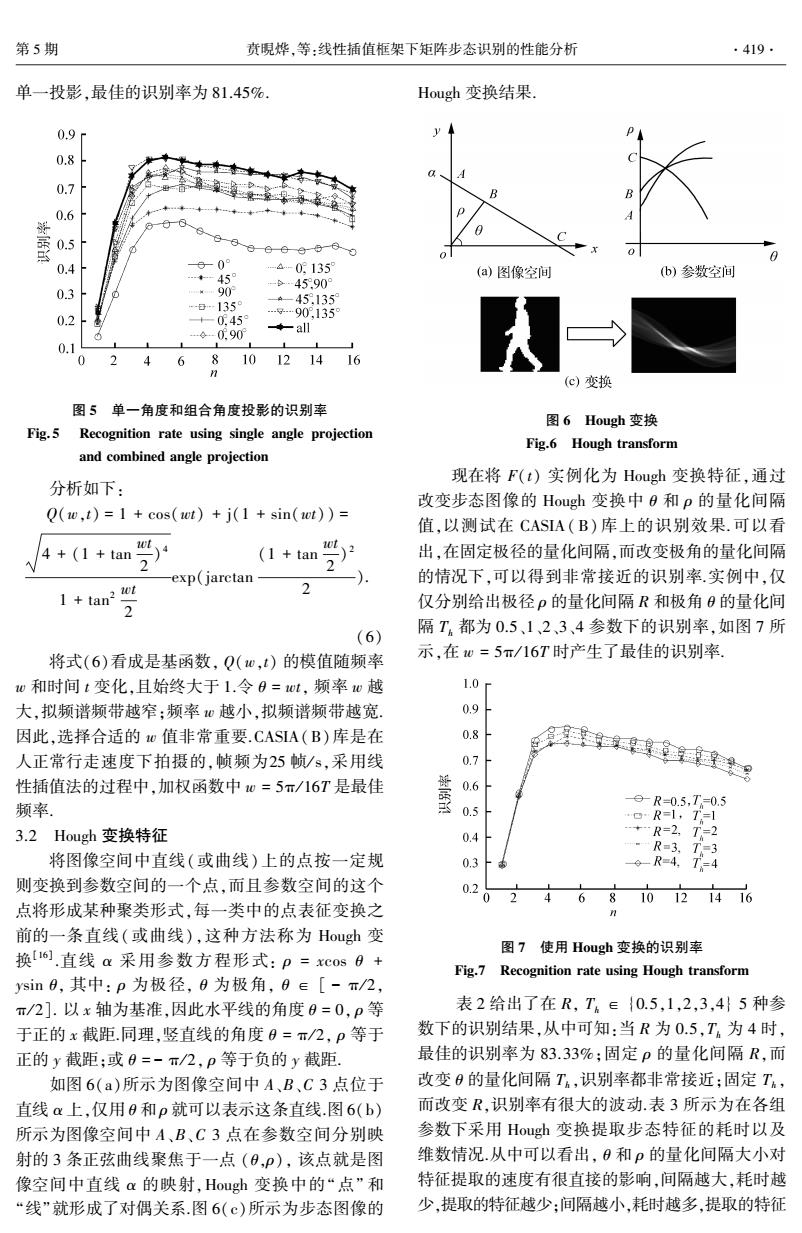
第5期 贲硯烨,等:线性插值框架下矩阵步态识别的性能分析 419. 单一投影,最佳的识别率为81.45%. Hough变换结果. 0.9r y 0.8 0.7 0.6 季 0.5 0 0.4 60° -4-0135 …◆-459 (a)图像空间 b)参数空间 -6-45909 0.3 -日…1359 445135 0.2 +-0.459 …g909,135 …g-0.90 ◆all 0.1 1 0 46810121416 (c)变换 图5单一角度和组合角度投影的识别率 图6 Hough变换 Fig.5 Recognition rate using single angle projection Fig.6 Hough transform and combined angle projection 现在将F(t)实例化为Hough变换特征,通过 分析如下: 改变步态图像的Hough变换中0和p的量化间隔 Q(w,t)=1 cos(wt)+j(1 sin(wt))= 值,以测试在CASIA(B)库上的识别效果.可以看 4+(1+tan2 1+am学 出,在固定极径的量化间隔,而改变极角的量化间隔 exp(jarctan 的情况下,可以得到非常接近的识别率.实例中,仅 1+tan? 2 仅分别给出极径p的量化间隔R和极角8的量化间 隔T都为0.5、1、2、3、4参数下的识别率,如图7所 (6) 将式(6)看成是基函数,Q(w,t)的模值随频率 示,在0=5π/16T时产生了最佳的识别率. w和时间t变化,且始终大于1.令0=wt,频率w越 1.0r 大,拟频谱频带越窄:频率心越小,拟频谱频带越宽. o 因此,选择合适的地值非常重要.CASIA(B)库是在 0.8 人正常行走速度下拍摄的,帧频为25帧/s,采用线 0.7 生痒g 性插值法的过程中,加权函数中0=5π/16T是最佳 薹 0.6 频率。 05 9R-0.5,T=0.5 oR=1,T=1 3.2 Hough变换特征 0.4 +R=2,T=2 R=3,T3 将图像空间中直线(或曲线)上的点按一定规 0.3 6-R=4,T4 则变换到参数空间的一个点,而且参数空间的这个 0.2 0 6 810121416 点将形成某种聚类形式,每一类中的点表征变换之 前的一条直线(或曲线),这种方法称为Hough变 换[16].直线a采用参数方程形式:p=xCos0+ 图7使用Hough变换的识别率 Fig.7 Recognition rate using Hough transform ysin0,其中:p为极径,0为极角,0e[-π/2, π/2].以x轴为基准,因此水平线的角度0=0,p等 表2给出了在R,T∈{0.5,1,2,3,4}5种参 于正的x截距.同理,竖直线的角度0=π/2,p等于 数下的识别结果,从中可知:当R为0.5,T。为4时, 正的y截距;或0=-π/2,p等于负的y截距. 最佳的识别率为83.33%;固定p的量化间隔R,而 如图6(a)所示为图像空间中A、B、C3点位于 改变0的量化间隔T,识别率都非常接近;固定T, 直线α上,仅用0和p就可以表示这条直线.图6(b) 而改变R,识别率有很大的波动.表3所示为在各组 所示为图像空间中A、B、C3点在参数空间分别映 参数下采用Hough变换提取步态特征的耗时以及 射的3条正弦曲线聚焦于一点(0,P),该点就是图 维数情况.从中可以看出,0和p的量化间隔大小对 像空间中直线α的映射,Hough变换中的“点”和 特征提取的速度有很直接的影响,间隔越大,耗时越 “线”就形成了对偶关系.图6(©)所示为步态图像的 少,提取的特征越少:间隔越小,耗时越多,提取的特征
单一投影ꎬ最佳的识别率为 81.45%. 图 5 单一角度和组合角度投影的识别率 Fig. 5 Recognition rate using single angle projection and combined angle projection 分析如下: Q(wꎬt) = 1 + cos(wt) + j(1 + sin(wt)) = 4 + (1 + tan wt 2 ) 4 1 + tan 2 wt 2 exp(jarctan (1 + tan wt 2 ) 2 2 ). (6) 将式(6)看成是基函数ꎬ Q(wꎬt) 的模值随频率 w 和时间 t 变化ꎬ且始终大于 1.令 θ = wtꎬ 频率 w 越 大ꎬ拟频谱频带越窄ꎻ频率 w 越小ꎬ拟频谱频带越宽. 因此ꎬ选择合适的 w 值非常重要.CASIA(B)库是在 人正常行走速度下拍摄的ꎬ帧频为25 帧/ sꎬ采用线 性插值法的过程中ꎬ加权函数中 w = 5π/ 16T 是最佳 频率. 3.2 Hough 变换特征 将图像空间中直线(或曲线) 上的点按一定规 则变换到参数空间的一个点ꎬ而且参数空间的这个 点将形成某种聚类形式ꎬ每一类中的点表征变换之 前的一条直线(或曲线)ꎬ这种方法称为 Hough 变 换[16] .直线 α 采用参数方程形式: ρ = xcos θ + ysin θꎬ 其中: ρ 为极径ꎬ θ 为极角ꎬ θ ∈ [ - π/ 2ꎬ π/ 2]. 以 x 轴为基准ꎬ因此水平线的角度 θ = 0ꎬ ρ 等 于正的 x 截距.同理ꎬ竖直线的角度 θ = π/ 2ꎬ ρ 等于 正的 y 截距ꎻ或 θ = - π/ 2ꎬ ρ 等于负的 y 截距. 如图 6(a)所示为图像空间中 A、B、C 3 点位于 直线 α 上ꎬ仅用 θ 和 ρ 就可以表示这条直线.图 6(b) 所示为图像空间中 A、B、C 3 点在参数空间分别映 射的 3 条正弦曲线聚焦于一点 (θꎬρ)ꎬ 该点就是图 像空间中直线 α 的映射ꎬHough 变换中的“点” 和 “线”就形成了对偶关系.图 6(c)所示为步态图像的 Hough 变换结果. 图 6 Hough 变换 Fig.6 Hough transform 现在将 F(t) 实例化为 Hough 变换特征ꎬ通过 改变步态图像的 Hough 变换中 θ 和 ρ 的量化间隔 值ꎬ以测试在 CASIA(B) 库上的识别效果. 可以看 出ꎬ在固定极径的量化间隔ꎬ而改变极角的量化间隔 的情况下ꎬ可以得到非常接近的识别率.实例中ꎬ仅 仅分别给出极径 ρ 的量化间隔 R 和极角 θ 的量化间 隔 Th 都为 0.5、1、2、3、4 参数下的识别率ꎬ如图 7 所 示ꎬ在 w = 5π/ 16T 时产生了最佳的识别率. 图 7 使用 Hough 变换的识别率 Fig.7 Recognition rate using Hough transform 表 2 给出了在 Rꎬ Th ∈ {0.5ꎬ1ꎬ2ꎬ3ꎬ4} 5 种参 数下的识别结果ꎬ从中可知:当 R 为 0.5ꎬTh 为 4 时ꎬ 最佳的识别率为 83.33%ꎻ固定 ρ 的量化间隔 Rꎬ而 改变 θ 的量化间隔 Th ꎬ识别率都非常接近ꎻ固定 Th ꎬ 而改变 Rꎬ识别率有很大的波动.表 3 所示为在各组 参数下采用 Hough 变换提取步态特征的耗时以及 维数情况.从中可以看出ꎬ θ 和 ρ 的量化间隔大小对 特征提取的速度有很直接的影响ꎬ间隔越大ꎬ耗时越 少ꎬ提取的特征越少ꎻ间隔越小ꎬ耗时越多ꎬ提取的特征 第 5 期 贲晛烨ꎬ等:线性插值框架下矩阵步态识别的性能分析 419