
第8卷第5期 智能系统学报 Vol.8 No.5 2013年10月 CAAI Transactions on Intelligent Systems 0ct.2013 D0:10.3969/j.issn.1673-4785.201212012 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.TP.20130929.1040.001.html 浸入与不变方法原理 及其在非线性自适应控制中的应用 刘振,谭湘敏,易建强,袁如意,范国梁 (中国科学院自动化研究所综合信息系统研究中心,北京100190) 摘要:非线性系统理论的实际工程需求和复杂性使其成为控制学科中最具吸引力和挑战性的研究领域,为此介绍 了一种新的非线性控制律设计方法一浸入与不变(I&)理论该方法首先选择一个比被控系统维数低的(局部)渐 近稳定的目标系统,然后设计浸入映射和控制律,使得原系统在控制律作用下的动态轨迹都是目标系统在浸入映射 下的像,并且该控制律能够保持目标系统的像为不变吸引流形,且使闭环轨迹有界.针对未知点质量模型,设计了一 种新的非线性浸入与不变自适应控制律,实现了对参考指令的精确跟踪将其与基于确定等价原则的自适应控制律 相比较,仿真结果表明,所设计的浸入与不变控制律能够更好地处理带有未知参数的系统 关键词:非线性控制:浸人与不变理论:自适应控制:控制律:未知点质量系统 中图分类号:TP273文献标志码:A文章编号:1673-4785(2013)05-0400-08 中文引用格式:刘振,谭湘敏,易建强,等浸入与不变方法原理及其在非线性自适应控制中的就用[J].智能系统学报,2013,8(5): 400-407. 英文引用格式:LIU Zhen,TAN Xiangmin,YI Jianqiang,etal.Immersion and invariance theory and its applications in nonlinear adaptive control[J].CAAI Transactions on Intelligent Systems,2013,8(5):400-407. Immersion and invariance theory and its application in nonlinear adaptive control LIU Zhen,TAN Xiangmin,YI Jiangiang,YUAN Ruyi,FAN Guoliang Integrated Information System Research Center,Institute of Automation,Chinese Academy of Sciences,Beijing 100190,China) Abstract:The actual engineering demands and the complexities of the nonlinear system theory have led it to become the most attractive and challenging research field in control subjects,therefore,a new nonlinear control law design method-immersion and invariance (I&I)theory has been introduced.With this method,a (partially)asymptoti- cally stable system with a dimension less than that of the controlled system is firstly selected as the target system, then the immersion mapping and control law are designed to make the controlled dynamics of the original system is an immersion image of the target system.In addition,the control law can keep the image of the target system as an invariant and attractive manifold,and render the trajectory of the closed-loop system bounded.Focusing on the un- known point mass model,a new nonlinear immersion and invariance adaptive control law is designed for realizing the precise tracking of a reference command.Compared with the adaptive control law based on the certainty-equiva- lent principle,the simulation results show that the proposed I&I adaptive control law is quite effective for processing a system with unknown parameters. Keywords:nonlinear control;immersion and invariance theory;adaptive control;control law;unknown point mass system 非线性是自然界和工程技术领域里普遍存在的 际工程对象进行精确建模.任何一个实际的物理系 现象.由于各种各样的原因,人们总是无法对一个实 统都是非线性的,而所谓的线性只是对非线性的一 种简化或近似,或说是非线性的一种特例.控制科学 收稿日期:2012-12-06.网络出版日期:2013-09-29. 发展至今,线性系统控制理论已经具有了相当完美 基金项目:国家自然科学基金资助项目(61273149,61203003):科技 部创新方法工作专项项目(2012M010200). 的理论框架,并且在工程实践中也有着成功的应用. 通信作者:谭湘敏.E-mail:minxiangtan(@163.com
第 8 卷第 5 期 智 能 系 统 学 报 Vol.8 №.5 2013 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2013 DOI:10.3969 / j.issn.1673 ̄4785.201212012 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20130929.1040.001.html 浸入与不变方法原理 及其在非线性自适应控制中的应用 刘振ꎬ谭湘敏ꎬ易建强ꎬ袁如意ꎬ范国梁 (中国科学院自动化研究所 综合信息系统研究中心ꎬ北京 100190) 摘 要:非线性系统理论的实际工程需求和复杂性使其成为控制学科中最具吸引力和挑战性的研究领域ꎬ为此介绍 了一种新的非线性控制律设计方法———浸入与不变(I&I)理论.该方法首先选择一个比被控系统维数低的(局部)渐 近稳定的目标系统ꎬ然后设计浸入映射和控制律ꎬ使得原系统在控制律作用下的动态轨迹都是目标系统在浸入映射 下的像ꎬ并且该控制律能够保持目标系统的像为不变吸引流形ꎬ且使闭环轨迹有界.针对未知点质量模型ꎬ设计了一 种新的非线性浸入与不变自适应控制律ꎬ实现了对参考指令的精确跟踪.将其与基于确定等价原则的自适应控制律 相比较ꎬ仿真结果表明ꎬ所设计的浸入与不变控制律能够更好地处理带有未知参数的系统. 关键词:非线性控制ꎻ浸入与不变理论ꎻ自适应控制ꎻ控制律ꎻ未知点质量系统 中图分类号:TP273 文献标志码:A 文章编号:1673 ̄4785(2013)05 ̄0400 ̄08 中文引用格式:刘振ꎬ谭湘敏ꎬ易建强ꎬ等.浸入与不变方法原理及其在非线性自适应控制中的就用[J]. 智能系统学报ꎬ 2013ꎬ 8(5): 400 ̄407. 英文引用格式:LIU Zhenꎬ TAN Xiangminꎬ YI Jianqiangꎬ et al. Immersion and invariance theory and its applications in nonlinear adaptive control[J]. CAAI Transactions on Intelligent Systemsꎬ 2013ꎬ 8(5): 400 ̄407. Immersion and invariance theory and its application in nonlinear adaptive control LIU Zhenꎬ TAN Xiangminꎬ YI Jianqiangꎬ YUAN Ruyiꎬ FAN Guoliang (Integrated Information System Research Centerꎬ Institute of Automationꎬ Chinese Academy of Sciencesꎬ Beijing 100190ꎬ China) Abstract:The actual engineering demands and the complexities of the nonlinear system theory have led it to become the most attractive and challenging research field in control subjectsꎬ thereforeꎬ a new nonlinear control law design method—immersion and invariance (I&I) theory has been introduced. With this methodꎬ a (partially) asymptoti ̄ cally stable system with a dimension less than that of the controlled system is firstly selected as the target systemꎬ then the immersion mapping and control law are designed to make the controlled dynamics of the original system is an immersion image of the target system. In additionꎬ the control law can keep the image of the target system as an invariant and attractive manifoldꎬ and render the trajectory of the closed ̄loop system bounded. Focusing on the un ̄ known point mass modelꎬ a new nonlinear immersion and invariance adaptive control law is designed for realizing the precise tracking of a reference command. Compared with the adaptive control law based on the certainty ̄equiva ̄ lent principleꎬ the simulation results show that the proposed I&I adaptive control law is quite effective for processing a system with unknown parameters. Keywords:nonlinear controlꎻ immersion and invariance theoryꎻ adaptive controlꎻ control lawꎻ unknown point mass system 收稿日期:2012 ̄12 ̄06. 网络出版日期:2013 ̄09 ̄29. 基金项目:国家自然科学基金资助项目( 61273149ꎬ61203003)ꎻ科技 部创新方法工作专项项目(2012IM010200). 通信作者:谭湘敏. E ̄mail: minxiangtan@ 163.com. 非线性是自然界和工程技术领域里普遍存在的 现象.由于各种各样的原因ꎬ人们总是无法对一个实 际工程对象进行精确建模.任何一个实际的物理系 统都是非线性的ꎬ而所谓的线性只是对非线性的一 种简化或近似ꎬ或说是非线性的一种特例.控制科学 发展至今ꎬ线性系统控制理论已经具有了相当完美 的理论框架ꎬ并且在工程实践中也有着成功的应用

第5期 刘振,等:浸入与不变方法原理及其在非线性自适应控制中的应用 ·401- 但其必须建立被控对象或过程的精确线性模型的局 假设3(隐流形)下面集合恒等成立: 限极大地制约了其进一步的发展.随着科学技术的 M={x(t)∈R"Ip(x)=0}= 进步,传统的线性控制理论已经越来越难以满足对 {x(t)∈R"Ix=π(5),专∈R}. 系统控制性能的要求;因此,对非线性系统控制理论 假设4(流形吸引性与轨迹有界性)存在系统 的研究,具有重要的理论意义和迫切的现实需求, 从20世纪80年代以来,非线性系统理论得到 i=2Ux)+g(x)(x,2), 了蓬勃的发展.这一期间,以A.Isidori教授为代表 x=f(x)+g(x)ψ(x,z), (3) 的非线性系统理论先驱们将微分几何等现代数学工 各个状态都是有界的,且满足: 具成功应用到控制理论中.正如他在文献[1]中所预 lim (t)=0. (4) 言:用微分几何法研究非线性系统所取得的成功,就 像50年代用拉氏变换及复变函数理论对单输入单 那么,x,就是闭环系统(5)的(局部)渐近稳定平衡 输出系统的研究,或60年代用线性代数对多变量系 点,也称为浸入与不变稳定 统的研究一样.微分几何方法的引入,给控制理论带 x=f(x)+g(x)(x,z). (5) 来了突破性进展,诸多基于微分几何方法的控制理 详细证明过程可参考文献[2-3]。 论被相继提出,并得到了广泛应用, 从上面的叙述中可以看出,一个系统的I&I镇 2003年,意大利学者A.Astol6等采用微分几何 定可以分2步实现首先,选择一个比原系统维数严 的概念提出了一种新的非线性系统控制方法一浸入 格低的(局部)渐近稳定的目标系统,找到一个浸入 与不变(immersion and invariance,l&I)[2).与通常 映射x=π(专),使得假设2成立;其次,设计控制 的非线性系统镇定需要Lyapunov函数不同,I&I方 律,使得流形M为不变吸引流形,并且闭环系统有 法不需要构造Lyapunov函数.该方法通过选择浸入 界.显然,应用&方法时,需要根据目标系统的选 映射和设计控制律,使得被控系统的任何轨迹都是 取,通过求解偏微分方程进而确定浸入映射π(·), 目标系统在该浸入映射下的像,并且设计的控制律 而这往往是比较困难的幸运的是,很多情况下根据 能够使目标系统的像为不变吸引流形,从而保证整 原系统和控制目标物理原理及系统理论的知识来选 个系统的稳定性该方法虽然提出时间不长,但由于 择目标系统可以大大简化该问题.该方法特别适用 其显著的非线性自适应性能,已经被广泛应用到各 于对被控对象的降阶系统设计稳定控制器的情 个方面s1本文专门讨论1&I方法的基本原理、设 形23].图1是1&I方法的一个形象描述,原系统是 计方法及其在自适应理论上的拓展,并将其应用到 一个n维系统(图中n=3),按照I&I理论,目标系 未知点质量系统的自适应控制上, 统可以选择1到n-1维任何一种情况.而基于Lya- 1 浸入与不变稳定理论 punov直接法的控制器设计方法可以看作是I&I方 法的一个特例,但设计控制律时需要选择Lyapunov 1.1基本原理 函数V(x),该函数正定且其导数7=ax(V)<0.从 设系统 I&I理论的角度看,I&I方法是将一个在原点渐近稳 x=f(x)+g(x)u. (1)》 定的一维目标系统V=α(V)浸入到高维的原系统中 式中:系统状态x∈R",输入u∈Rm, 1维目标系统 考虑系统(1)的镇定问题,即寻找状态反馈控 (如渐进收敛的Lyapunov函数系统) 制律u=v(x),使x.为闭环系统的(局部)渐近稳 n维原系统 0P-a0<0g 定平衡点.假设存在如下映射: x-Ax)+g(x)u Tx ()系统浸入 a(·):R”→R,T(·):R”→R",c(·):R→Rm, 2维日标系统 π(). p():R"→R"P,(·,·):Rax(ap)→Rm, n-l维目标系统 其中p<n,使得下面的4个假设成立[创 () ξ=a(5) 系统浸入 假设1(目标系统)存在系统专=α(专),专∈ 全局吸引的 不变流形亚() R”,具有(局部)渐近稳定平衡点专。,且x。= π(5,) 假设2(浸入条件)对于所有专∈R”,有 图1浸入与不变方法 dT Fig.1 Graphical illustration of the immersion and in- f八π())+g(π())c(π(专))= 话a(5).(2) variance approach
但其必须建立被控对象或过程的精确线性模型的局 限极大地制约了其进一步的发展.随着科学技术的 进步ꎬ传统的线性控制理论已经越来越难以满足对 系统控制性能的要求ꎻ因此ꎬ对非线性系统控制理论 的研究ꎬ具有重要的理论意义和迫切的现实需求. 从 20 世纪 80 年代以来ꎬ非线性系统理论得到 了蓬勃的发展.这一期间ꎬ以 A. Isidori 教授为代表 的非线性系统理论先驱们将微分几何等现代数学工 具成功应用到控制理论中.正如他在文献[1]中所预 言:用微分几何法研究非线性系统所取得的成功ꎬ就 像 50 年代用拉氏变换及复变函数理论对单输入单 输出系统的研究ꎬ或 60 年代用线性代数对多变量系 统的研究一样.微分几何方法的引入ꎬ给控制理论带 来了突破性进展ꎬ诸多基于微分几何方法的控制理 论被相继提出ꎬ并得到了广泛应用. 2003 年ꎬ意大利学者 A. Astolfi 等采用微分几何 的概念提出了一种新的非线性系统控制方法—浸入 与不变( immersion and invarianceꎬ I&I) [2 ̄4] .与通常 的非线性系统镇定需要 Lyapunov 函数不同ꎬI&I 方 法不需要构造 Lyapunov 函数.该方法通过选择浸入 映射和设计控制律ꎬ使得被控系统的任何轨迹都是 目标系统在该浸入映射下的像ꎬ并且设计的控制律 能够使目标系统的像为不变吸引流形ꎬ从而保证整 个系统的稳定性.该方法虽然提出时间不长ꎬ但由于 其显著的非线性自适应性能ꎬ已经被广泛应用到各 个方面[5 ̄12] .本文专门讨论 I&I 方法的基本原理、设 计方法及其在自适应理论上的拓展ꎬ并将其应用到 未知点质量系统的自适应控制上. 1 浸入与不变稳定理论 1.1 基本原理 设系统 ̇x = f(x) + g(x)u. (1) 式中:系统状态 x ∈ R n ꎬ输入 u ∈ R m . 考虑系统(1)的镇定问题ꎬ即寻找状态反馈控 制律 u = v(x) ꎬ使 x∗ 为闭环系统的(局部)渐近稳 定平衡点.假设存在如下映射: α():R p → R p ꎬπ():R p → R n ꎬc():R p → R m ꎬ φ():R n → R n-p ꎬψ(ꎬ):R n×(n-p) → R m ꎬ 其中 p < n ꎬ使得下面的 4 个假设成立[3] . 假设 1(目标系统) 存在系统 ̇ξ =α(ξ)ꎬξ ∈ R p ꎬ 具有 ( 局 部) 渐 近 稳 定 平 衡 点 ξ∗ꎬ 且 x∗ = π(ξ ∗) . 假设 2(浸入条件) 对于所有 ξ ∈ R p ꎬ 有 f(π(ξ) ) + g(π(ξ) ) c(π(ξ) ) = ∂π ∂ξ α(ξ). (2) 假设 3(隐流形) 下面集合恒等成立: M = x(t) ∈ R n { | φ(x) = 0} = x(t) ∈ R n | x = π(ξ)ꎬ ξ ∈ R p { } . 假设 4(流形吸引性与轨迹有界性) 存在系统 ̇z = ∂φ ∂x (f(x) + g(x)ψ(xꎬz))ꎬ ̇x = f(x) + g(x)ψ(xꎬz)ꎬ (3) 各个状态都是有界的ꎬ且满足: lim t→¥ z(t) = 0. (4) 那么ꎬx∗就是闭环系统(5)的(局部)渐近稳定平衡 点ꎬ也称为浸入与不变稳定. ̇x = f(x) + g(x)ψ(xꎬz). (5) 详细证明过程可参考文献[2 ̄3]. 从上面的叙述中可以看出ꎬ一个系统的 I&I 镇 定可以分 2 步实现.首先ꎬ选择一个比原系统维数严 格低的(局部)渐近稳定的目标系统ꎬ找到一个浸入 映射 x = π(ξ)ꎬ 使得假设 2 成立ꎻ其次ꎬ设计控制 律ꎬ使得流形 M 为不变吸引流形ꎬ并且闭环系统有 界.显然ꎬ应用 I&I 方法时ꎬ需要根据目标系统的选 取ꎬ通过求解偏微分方程进而确定浸入映射 π()ꎬ 而这往往是比较困难的.幸运的是ꎬ很多情况下根据 原系统和控制目标物理原理及系统理论的知识来选 择目标系统可以大大简化该问题.该方法特别适用 于对被控对象的降阶系统设计稳定控制器的情 形[2 ̄3] .图 1 是 I&I 方法的一个形象描述ꎬ原系统是 一个 n 维系统(图中 n = 3)ꎬ按照 I&I 理论ꎬ目标系 统可以选择 1 到 n-1 维任何一种情况.而基于 Lya ̄ punov 直接法的控制器设计方法可以看作是 I&I 方 法的一个特例ꎬ但设计控制律时需要选择Lyapunov 函数 V(x)ꎬ 该函数正定且其导数 V = α(V) < 0.从 I&I 理论的角度看ꎬI&I 方法是将一个在原点渐近稳 定的一维目标系统 V = α(V) 浸入到高维的原系统中. 图 1 浸入与不变方法 Fig.1 Graphical illustration of the immersion and in ̄ variance approach 第 5 期 刘振ꎬ等:浸入与不变方法原理及其在非线性自适应控制中的应用 401
·402· 智能系统学报 第8卷 1.2简单示例 按照上述的推导过程,可取 下面通过一个简单的例子来详细说明I&I镇定 K(x1,)=rxi+2. 的方法考虑系统: 式中:1≥1,12>0最终的1&I镇定控制律为 x1=f八x1,x2)=-x1-xi+x1x2, 山1=-(T1x+T2)x2 (6) (x2=u. 另外,原系统(6)的状态方程显然满足“下三 角”形式,因此可参考文献[l3],设计一种Backstep 式中:系统状态x=(x1,x,)T∈R,控制输入u∈R. ping控制律为 简单地计算可以得出,=(x,0)=-x1-x在 u=-2x-3x2+2x-2xx2 原点是渐近稳定的,因此可取目标系统为专=一专- 2种控制律的仿真结果如图2~4所示.初始状 (参考文献[2],这是对于此类系统选取目标系统 态都选为x=(4,3),其中图2和图3中I&I控制 的通常方法) 律的参数选为r1=1,2=2.可以看出,采用I&I方法 选择π,()=专,则偏微分方程(2)可以记为 设计的控制律不仅形式更为简单,而且镇定效果也 -ξ-E+π2(5)E=-5-53, 很出色.图4是I&I方法在不同参数下对应的状态 aπ2(5) 轨迹图,阴影部分代表不变流形z=0,轨迹图显示 ()= 出不同参数下该流形都具有不变性和吸引性. 通过第1个方程求出π2()=0.因此隐流形可以表 6 示为p(x)=x2: …Backstepping控制律 至此,假设1、假设2和假设3都已验证成立.根 1&1控制律 据式(3),流形外(off-he-manifold)动态方程可以表 示为:=元2=山.取u=-K(x1,x)z,其中K(x1, 6 P 10 x2)≥k>0,于是闭环系统的状态方程可以表示为 tis (a)状态x, 1=-1-x+x2, 15 x2=-K(x1,x2)x2, (7) 10 --…Backstepping控制律 1&I控制律 2=-K(x1,x2)z. 从式(7)的最后2个方程可以看出x2和z收敛 到零,因此式(4)成立.下面只需证明x,有界即可完 41s6 10 成I&I镇定设计.取 12 b)状态x W(1,x2)=V(x)+2近, 图2状态x的变化曲线 求导得 Fig.2 Time histories of the states x ×10 3 /,0)+ av W= av ,-K(x,x)x≤ --Backstepping控制律 I&I控制律 ,0)+y(x,)+ axi 1 av2 4 6 8 10 (8) tis y(x1)ax -K(x1,x2)x2 (a)全局 式中:y(x1)>0. ×10 取V(x1)=x/2,简单地推导可以得出,当取 -…Backstepping控制律 y(x1)=1,K(x1,x2)-x>0时,有W<0.至此可 一1&I控制律 证明x,有界,于是假设4成立.从式(8)可以看出, V(x1)不必选取x,=f八x1,0)的Lyapunov函数,而只 0.04 0.080.12 0.160.20 t/s 需保证V(x1)≥0,然后适当选取y和K使W<0即 (b)局部 可.在某些情况下,保证后者要比选取Lyapunov函 图3输入u的变化曲线 数简单 Fig.3 Time histories of the control input u
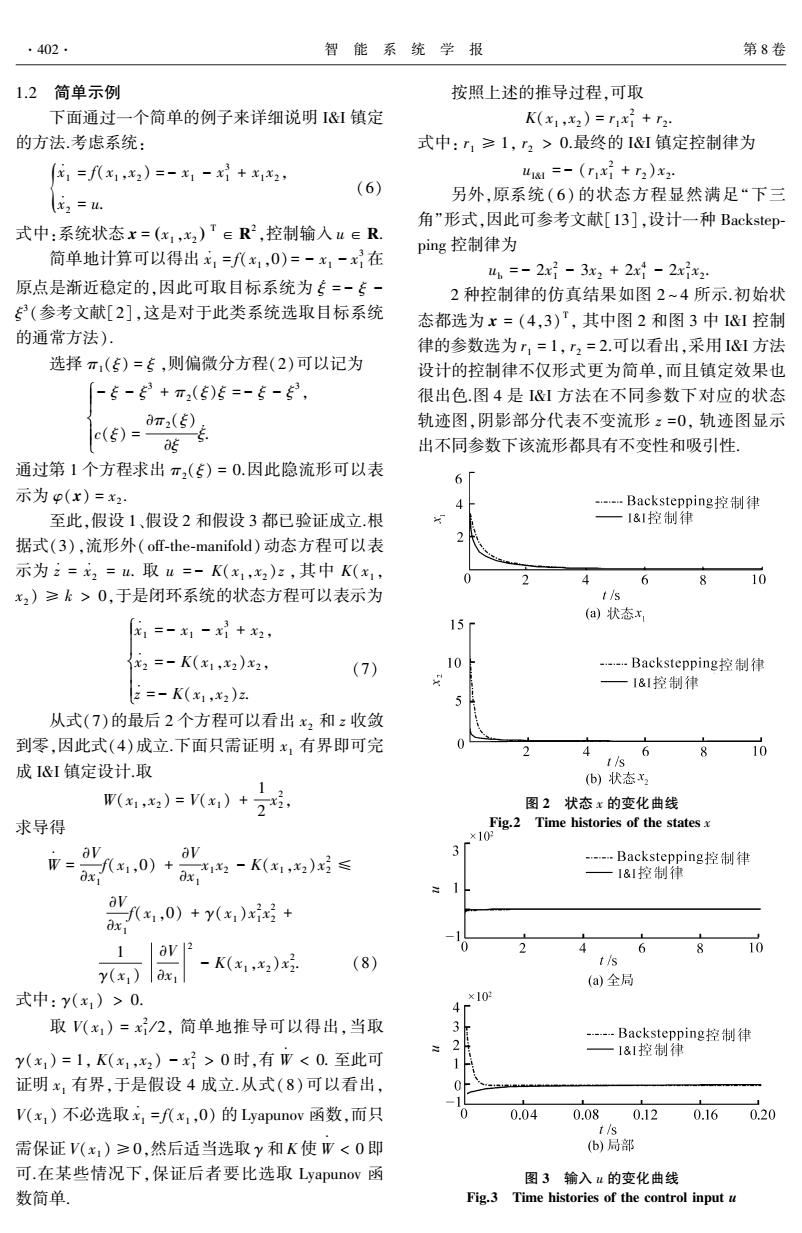
1.2 简单示例 下面通过一个简单的例子来详细说明 I&I 镇定 的方法.考虑系统: ̇x1 = f(x1 ꎬx2 ) = - x1 - x 3 1 + x1 x2 ꎬ ̇x2 { = u. (6) 式中:系统状态 x = x1 ꎬx2 ( ) T ∈ R 2 ꎬ控制输入 u ∈ R. 简单地计算可以得出 ̇x1 = f(x1 ꎬ0) = - x1 - x 3 1 在 原点是渐近稳定的ꎬ因此可取目标系统为 ̇ξ = - ξ - ξ 3 (参考文献[2]ꎬ这是对于此类系统选取目标系统 的通常方法). 选择 π1(ξ) = ξ ꎬ则偏微分方程(2)可以记为 - ξ - ξ 3 + π2(ξ)ξ = - ξ - ξ 3 ꎬ c(ξ) = ∂π2(ξ) ∂ξ ̇ξ. ì î í ï ï ïï 通过第 1 个方程求出 π2(ξ) = 0.因此隐流形可以表 示为 φ(x) = x2 . 至此ꎬ假设 1、假设 2 和假设 3 都已验证成立.根 据式(3)ꎬ流形外(off ̄the ̄manifold)动态方程可以表 示为 ̇ z = ̇x2 = u. 取 u = - K(x1 ꎬx2 )z ꎬ其中 K(x1 ꎬ x2 ) ≥ k > 0ꎬ于是闭环系统的状态方程可以表示为 ̇x1 = - x1 - x 3 1 + x2 ꎬ ̇x2 = - K(x1 ꎬx2 )x2 ꎬ ̇ z = - K(x1 ꎬx2 )z. ì î í ï ï ï ï (7) 从式(7)的最后 2 个方程可以看出 x2 和 z 收敛 到零ꎬ因此式(4)成立.下面只需证明 x1 有界即可完 成 I&I 镇定设计.取 W(x1 ꎬx2 ) = V(x1 ) + 1 2 x 2 2 ꎬ 求导得 W = ∂V ∂x1 f(x1 ꎬ0) + ∂V ∂x1 x1 x2 - K(x1 ꎬx2 )x 2 2 ≤ ∂V ∂x1 f(x1 ꎬ0) + γ(x1 )x 2 1 x 2 2 + 1 γ(x1 ) ∂V ∂x1 2 - K(x1 ꎬx2 )x 2 2 . (8) 式中: γ(x1 ) > 0. 取 V(x1 ) = x 2 1 / 2ꎬ 简单地推导可以得出ꎬ当取 γ(x1 ) = 1ꎬ K(x1 ꎬx2 ) - x 2 1 > 0 时ꎬ有 W < 0. 至此可 证明 x1 有界ꎬ于是假设 4 成立.从式(8)可以看出ꎬ V(x1 ) 不必选取 ̇x1 = f(x1 ꎬ0) 的 Lyapunov 函数ꎬ而只 需保证 V(x1 ) ≥0ꎬ然后适当选取 γ 和 K 使 W < 0 即 可.在某些情况下ꎬ保证后者要比选取 Lyapunov 函 数简单. 按照上述的推导过程ꎬ可取 K(x1 ꎬx2 ) = r1 x 2 1 + r2 . 式中: r1 ≥ 1ꎬ r2 > 0.最终的 I&I 镇定控制律为 uI&I = - (r1 x 2 1 + r2 )x2 . 另外ꎬ原系统( 6) 的状态方程显然满足“下三 角”形式ꎬ因此可参考文献[13]ꎬ设计一种 Backstep ̄ ping 控制律为 ub = - 2x 2 1 - 3x2 + 2x 4 1 - 2x 2 1 x2 . 2 种控制律的仿真结果如图 2 ~ 4 所示.初始状 态都选为 x = (4ꎬ3) T ꎬ 其中图 2 和图 3 中 I&I 控制 律的参数选为 r1 = 1ꎬ r2 = 2.可以看出ꎬ采用 I&I 方法 设计的控制律不仅形式更为简单ꎬ而且镇定效果也 很出色.图 4 是 I&I 方法在不同参数下对应的状态 轨迹图ꎬ阴影部分代表不变流形 z =0ꎬ 轨迹图显示 出不同参数下该流形都具有不变性和吸引性. 图 2 状态 x 的变化曲线 Fig.2 Time histories of the states x 图 3 输入 u 的变化曲线 Fig.3 Time histories of the control input u 402 智 能 系 统 学 报 第 8 卷

第5期 刘振,等:浸入与不变方法原理及其在非线性自适应控制中的应用 ·403. 制方法与传统的基于确定等价原则的自适应控制方 -片=1.'2=2 法的不同。 -…1=5,2=2 …=1.2=5 考虑系统: x=01x2+02x+u. (9) 0 式中:日,02∈R是未知常数,设计控制律使闭环系 -1 统(9)在原点渐近稳定平衡. 4 如果采用基于确定等价原则的自适应控制方 2 法,可以设计状态反馈控制律和参数估计自适应律: 1 2 3 0 0 u=-0x2-02x-cx, 61=w1,a2=w2 图4状态轨迹 Fig.4 Trajectories of the states 式中:c>0.选择Lyapunov函数: 2浸入与不变自适应控制 Wxa.4)=+ 2(0-8,)2+ 2.1基本原理 2(0-6)3 1 对于系统(1),若函数f(·)和g(·)中含有未 式中:r1>0,12>0,求导整理得 知参数0∈R?,那么系统的镇定问题就变成含有未 知参数的自适应控制问题.定义如下假设: V=(0,-0)(x3-r1w)+ 假设5(可镇定性) 存在一个参数化的函数 (02-02)(x2-r2w2)-cx2 v(x,0),0∈R,使得系统 因此自适应律可以选为 x=f.(x)Af(x)+g(x)v(x,0) 13 01 有一个全局渐近稳定的平衡点x=x 如果系统(1)满足假设5,并且能找到函数 ,=2 B(·)和ω(·),使得如下扩展系统: (x=f(x)+g(x)v(x,0+B(x)), 此时有V=-cx2. i=w(x,0). 上述方法可以保证(x,0,02)=0是全局渐近 关于目标系统:专=f.()是I&I稳定的,那么系 稳定的.但它的一个缺点是参数估计误差-日的动 统(1)就被称为自适应浸入与不变(I&I)可镇定 态变化过程无法调节,而这一估计误差有时会严重 的 影响到闭环系统的瞬态响应.而&I自适应镇定可 在I&I自适应方法中,系统的未知参数0用0+ 以很好地解决这个问题。 B(x)来估计,相比传统的基于确定等价原则的自适 考虑如下扩展系统: 应控制方法多出额外一项B(x).B(x)的引入使得 x=0x2+02x+u, 整个参数估计律由单一的积分作用转变为比例积分 作用,设计估计律时更加灵活有效.另外,&I理论通 a=: (10) 过保持流形的不变性与吸引性来保证整个系统的稳 02=0: 定性,该思想同样也可以应用到参数估计自适应律 定义流形: 的设计上.通常在I&I自适应设计中选取未知参数 M={(x,01,02)∈R310,-01+B,(x)=0, 的估计值和真实值之间的差值作为不变流形,通过 保持该流形的不变与吸引性,可以保证估计误差有 02-02+B2(x)=0} 界甚至收敛到零。 式中:B,(x)和B2(x)是待选取的函数.若该流形能 2.2简单示例 够保持不变性,系统(10)的第1个式子可以表示为 下面通过一个简单的例子来说明I&I自适应控 x=(a+B,(x))x2+(a2+B2(x)x+u.(11)
图 4 状态轨迹 Fig.4 Trajectories of the states 2 浸入与不变自适应控制 2.1 基本原理 对于系统(1)ꎬ若函数 f() 和 g() 中含有未 知参数 θ ∈ R q ꎬ那么系统的镇定问题就变成含有未 知参数的自适应控制问题.定义如下假设: 假设 5(可镇定性) 存在一个参数化的函数 υ(xꎬθ)ꎬ θ ∈ R q ꎬ使得系统 x = f∗(x) f(x) + g(x)υ(xꎬθ) 有一个全局渐近稳定的平衡点 x = x∗. 如果系统 ( 1) 满足假设 5ꎬ 并且能找到函数 β() 和 ω()ꎬ 使得如下扩展系统: : x = f(x) + g(x)υ(xꎬθ ^ + β(x))ꎬ θ ^ = ω(xꎬθ ^ ). { 关于目标系统 ΣT : ̇ξ = f∗(ξ) 是 I&I 稳定的ꎬ那么系 统(1) 就被称为自适应浸入与不变( I&I) 可镇定 的[2] . 在 I&I 自适应方法中ꎬ系统的未知参数 θ 用 θ ^ + β(x) 来估计ꎬ相比传统的基于确定等价原则的自适 应控制方法多出额外一项 β(x). β(x) 的引入使得 整个参数估计律由单一的积分作用转变为比例积分 作用ꎬ设计估计律时更加灵活有效.另外ꎬI&I 理论通 过保持流形的不变性与吸引性来保证整个系统的稳 定性ꎬ该思想同样也可以应用到参数估计自适应律 的设计上.通常在 I&I 自适应设计中选取未知参数 的估计值和真实值之间的差值作为不变流形ꎬ通过 保持该流形的不变与吸引性ꎬ可以保证估计误差有 界甚至收敛到零. 2.2 简单示例 下面通过一个简单的例子来说明 I&I 自适应控 制方法与传统的基于确定等价原则的自适应控制方 法的不同. 考虑系统: ̇x = θ1 x 2 + θ2 x + u. (9) 式中: θ1 ꎬθ2 ∈ R 是未知常数ꎬ设计控制律使闭环系 统(9)在原点渐近稳定平衡. 如果采用基于确定等价原则的自适应控制方 法ꎬ可以设计状态反馈控制律和参数估计自适应律: u = - ^θ1 x 2 - ^θ2 x - cxꎬ ^θ 1 = ω1 ꎬ ^θ 2 = ω2 . ì î í ïï ï 式中: c > 0.选择 Lyapunov 函数: V(xꎬ ^θ1 ꎬ ^θ2 ) = 1 2 x 2 + 1 2 r1 ( ^θ1 - θ1 ) 2 + 1 2 r2 ( ^θ2 - θ2 ) 2 . 式中: r1 > 0ꎬr2 > 0ꎬ求导整理得 V = ( ^θ1 - θ1 )(x 3 - r1ω1 ) + ( ^θ2 - θ2 )(x 2 - r2ω2 ) - cx 2 . 因此自适应律可以选为 ω1 = 1 r1 x 3 ꎬ ω2 = 1 r2 x 2 . ì î í ï ïï ï ï 此时有 V = - cx 2 . 上述方法可以保证 (xꎬ ^θ1 ꎬ ^θ2 ) = 0 是全局渐近 稳定的.但它的一个缺点是参数估计误差 ^θ - θ 的动 态变化过程无法调节ꎬ而这一估计误差有时会严重 影响到闭环系统的瞬态响应.而 I&I 自适应镇定可 以很好地解决这个问题. 考虑如下扩展系统: ̇x = θ1 x 2 + θ2 x + uꎬ ^θ 1 = ω1 ꎬ ^θ 2 = ω2 . ì î í ï ï ï ï ïï (10) 定义流形: M = (xꎬ ^θ1 ꎬ ^θ2 ) ∈ R 3 | ^θ1 - θ 1 { + β1(x) = 0ꎬ ^θ2 - θ 2 + β2(x) = 0} . 式中: β1(x) 和 β2(x) 是待选取的函数.若该流形能 够保持不变性ꎬ系统(10)的第 1 个式子可以表示为 ̇x = ( ^θ1 + β1(x))x 2 + ( ^θ2 + β2(x))x + u. (11) 第 5 期 刘振ꎬ等:浸入与不变方法原理及其在非线性自适应控制中的应用 403
·404 智能系统学报 第8卷 此时,系统(11)中的各个参数都是已知的,因 式中:r>0,代入式(16),有 此可以设计控制律: V=-r(z1x2+2x)2≤0 u=-cx-(01+B,(x))x2-(02+B2(x)x 至此,采用I&I自适应方法的控制律设计完毕 式中:c>0. 2种控制律的仿真结果如图5和图6.初始状态 现在只需设计自适应律ω1、ω2和额外项 为x=3,未知参数的真值为(01,02)=(5,3),但初 B,(x)、B2(x),使得M流形具有不变性和吸引性, 始估计值都选为零.基于确定等价原则的自适应控 就可以保证闭环系统在原点是渐近稳定的流形外 制律参数选为71=r2=1,c=2,1&I自适应控制律参 数选为r=1,c=2.从图中可以看出,I&I自适应控制 的方程为 器比传统的自适应控制器镇定效果更佳,而且对未 1=a-01+B,(x), 知参数的估计也更为准确.需要说明的是,&I自适 (12) a2=02-02+B2(x). 应控制中,参数估计值并不能绝对收敛到真值,有关 这个问题可参见文献[12,14] 对式(12)求导,得 那(x) 6 =0+ (0,+B,(x)-1)x2+ …传统自适应控制 Ox 18I自适应控制 (02+B,(x)-22)x+u), (13) aβ2(x) 2=w2+ ar(8,+B,()-)2+ 0 0.51.01.52.0 2.53.0 3.54.0 t/s (02+B2(x)-22)x+u) (a)状态x 选取 -50 …传统自适应控制 aB,(x) (a+B(x)x2+(a+B2(x)x+u), -100 一1&自适应控制 x -1505 B2(x) -200月 (色+B,(x)x2+(a,+B,(x)x+u). ax -250 0.51.01.52.02.53.03.54.0 (14) 11s 将式(14)代入式(13),得 (b)输人u aB (x) 图5状态x及输入u的变化曲线 21 Ox (ax2+2x), Fig.5 Time histories of the states x and the control input u (15) a那2(x) (z1x2+z2x). 15r 对于式(l5),考虑Lyapunov函数: 10 传统自适应控制 I&I自适应控制 1 V(z1,2)= 0 0.51.01.52.02.53.03.54.0 有 t/s =-9,(x) (a)参数估计0 (21x2+22x)a1- ax a那2(x (21x2+2x)22 (16) Ox …传统自适应控制 取 一1&1自适应控制 aB,(x) 0 0.51.01.52.02.53.03.54.0 =x2, t/s dx (b)参数估计a, aβ2(x) =rX. 图6参数估计曲线 ax Fig.6 Parameter estimate curves
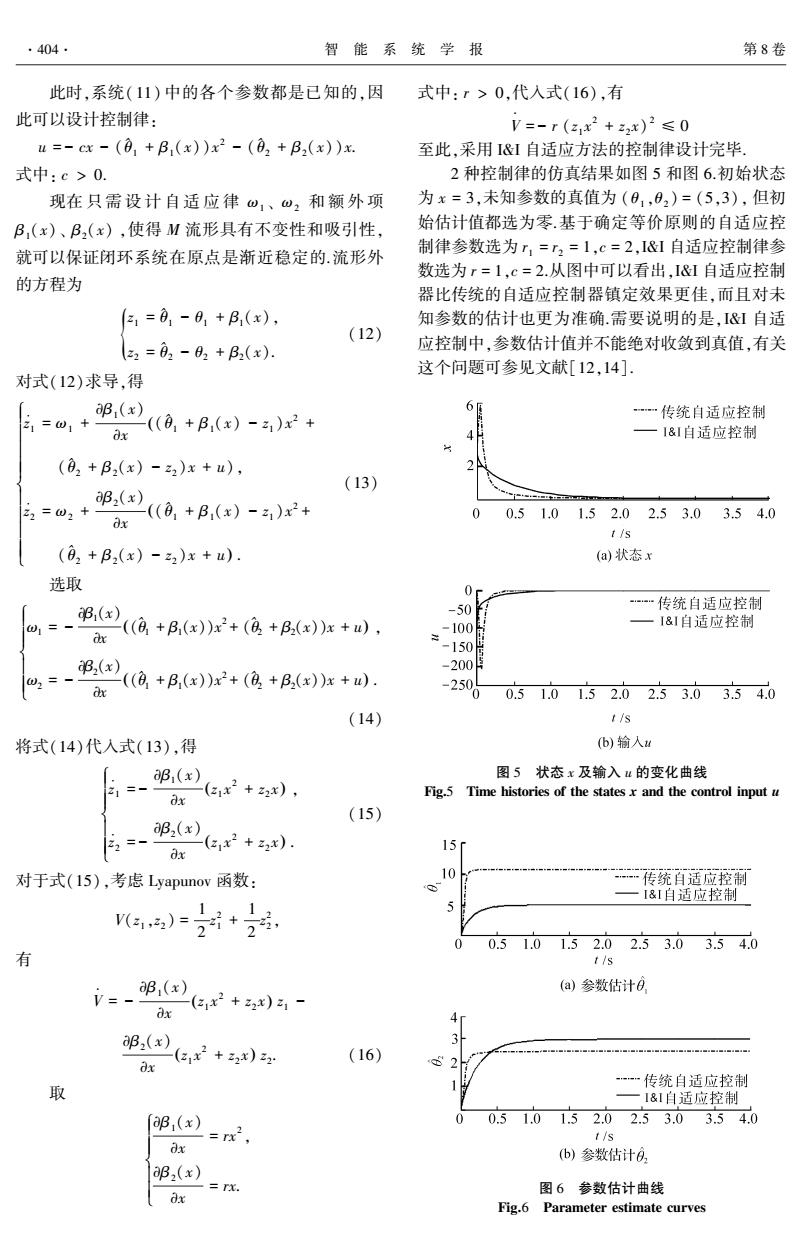
此时ꎬ系统(11) 中的各个参数都是已知的ꎬ因 此可以设计控制律: u = - cx - ( ^θ1 + β1(x))x 2 - ( ^θ2 + β2(x))x. 式中: c > 0. 现在 只 需 设 计 自 适 应 律 ω1 、 ω2 和 额 外 项 β1(x)、 β2(x) ꎬ使得 M 流形具有不变性和吸引性ꎬ 就可以保证闭环系统在原点是渐近稳定的.流形外 的方程为 z1 = ^θ1 - θ1 + β1(x)ꎬ z2 = ^θ2 - θ2 { + β2(x). (12) 对式(12)求导ꎬ得 ̇ z1 = ω1 + ∂β1(x) ∂x ( ^θ1 + β1(x) - z1 )x 2 ( + ( ^θ2 + β2(x) - z2 )x + u)ꎬ ̇ z2 = ω2 + ∂β2(x) ∂x ( ^θ1 + β1(x) - z1 )x 2 ( + ( ^θ2 + β2(x) - z2 )x + u) . ì î í ï ï ï ïï ï ï ï ïï (13) 选取 ω1 = - ∂β1(x) ∂x ( ^θ1 + β1(x))x 2 ( + ( ^θ2 + β2(x))x + u) ꎬ ω2 = - ∂β2(x) ∂x ( ^θ1 + β1(x))x 2 ( + ( ^θ2 + β2(x))x + u) . ì î í ï ïï ï ï (14) 将式(14)代入式(13)ꎬ得 ̇ z1 = - ∂β1(x) ∂x z1 x 2 + z2 ( x) ꎬ ̇ z2 = - ∂β2(x) ∂x z1 x 2 + z2 ( x) . ì î í ï ïï ï ï (15) 对于式(15)ꎬ考虑 Lyapunov 函数: V(z1 ꎬz2 ) = 1 2 z 2 1 + 1 2 z 2 2 ꎬ 有 V = - ∂β1(x) ∂x z1 x 2 + z2 ( x) z1 - ∂β2(x) ∂x z1 x 2 + z2 ( x) z2 . (16) 取 ∂β1(x) ∂x = rx 2 ꎬ ∂β2(x) ∂x = rx. ì î í ï ïï ï ï 式中: r > 0ꎬ代入式(16)ꎬ有 V = - r (z1 x 2 + z2 x) 2 ≤ 0 至此ꎬ采用 I&I 自适应方法的控制律设计完毕. 2 种控制律的仿真结果如图 5 和图 6.初始状态 为 x = 3ꎬ未知参数的真值为 (θ 1 ꎬθ 2 ) = (5ꎬ3)ꎬ 但初 始估计值都选为零.基于确定等价原则的自适应控 制律参数选为 r1 = r2 = 1ꎬc = 2ꎬI&I 自适应控制律参 数选为 r = 1ꎬc = 2.从图中可以看出ꎬI&I 自适应控制 器比传统的自适应控制器镇定效果更佳ꎬ而且对未 知参数的估计也更为准确.需要说明的是ꎬI&I 自适 应控制中ꎬ参数估计值并不能绝对收敛到真值ꎬ有关 这个问题可参见文献[12ꎬ14]. 图 5 状态 x 及输入 u 的变化曲线 Fig.5 Time histories of the states x and the control input u 图 6 参数估计曲线 Fig.6 Parameter estimate curves 404 智 能 系 统 学 报 第 8 卷