
物理化学解题思路和方法 又因为是循环过程体系熵变为0,即 △S体=0 所以 △S=△S体+△S环<0 这一结果显然违背了嫡增加原理,因此是假设不能成立,故Clausius说法是正确的. 【例1.2-2】今有0.1mol液体乙醚和0.397molN2(g),在308K、p°,它们占有体积为 10dm3.现经一等温过程后,乙醚液体全部气化,气体混合物可视为理想混合气体,其体积仍为 10dm3.求始态和终态体系熵差及过程的性质(已知p°、308K乙醚气化热为25.104k·mol-, 乙酵的正常沸点为308K) 解析308K是乙醚正常沸点,但在本题条件下上述过程并不是平衡相变,因为终态压力 显然不会是力°.但我们可以利用状态函数特点,将原过程分为三个可逆过程(见图18). 乙鞋045乙Ahs乙陆(4s 0.1mod乙雕(g) 308K 308K 308K p9 0.397 mol Na(g L308K,10dm3 图1-8 过程①为等温等压平衡相变 △s=H,A5=0lx25104·K1=8.149J·K 308 过程②为理想气体等温可逆膨胀 p==0.1×8314×308=25607Pa 10×103 45=aRn102592=1.143JK 过程③为308K,10dm3的乙酵(g)和308K、10dm3的八2(g)混合.根据理想气体等温等 容混合公式,△S=0. 总的过程 △S体=△1S+△2S+△3S=9.29JK1 △S环的求算关键在于求实际过程中体系吸的热量.这时就不能用所设计的三个过程的方 法来求(为什么?).因为实际过程为等容过程,所以 △S乐=-号=-'=-4H-A(pY -H eVBv ≈-9+7 =(-8.149+0.83月·K-1 =-7.32J·K-‘ 计算中忽略了液体体积,所以 △S=△S体+△S环=1.97J小K-1>0 根据嫡增加原理,判定该过程为不可逆过程. 22

第1章热力学基本定律 问题(1)为何在计算△S环中,△H等于设计过程中△H?(2)此题可否用△F判断过 程方向性? 【例1.23】计算图19所示各过程中理想气体的熵变,其中(5)图是抽去中间隔板, (6)图是等温下抽去中间隔板。 (1)等温 1 mol N2 nol A 1 mol N2+1 mol Ar (2)等温 2 mol N2 (3)等温 mol N 1 mol Ar 1 mol N2+1mol Ar (4)等温 mol N 1 mol N 2 mol N2 (5)绝热 1 mol O2.1 mol Na 293K 288K (6) 1 mol N2 2 mol N2 3 mol N2 T20T 力,几 图1-9 解析(1)该过程为等温等压混合过程,则 △S=-nR1n}+ln2)=2Rn2=11.53JK1 (2)该过程为同种气体等温等压混合,△S=0,混合前后气体状态未变 (3)过程为等温等容混合,△S=0. (4)过程可看做理想气体等温压缩过程,混合前后气体状态发生了改变.压力由p→2p, 体积由2V→V. △S=nRin(p/p=2×8.314×ln7J·K-1=-11.53J·K-1 (5)过程可设想为:(i)通过透热壁传热,终态温度为288K,其熵变为△1S;()然后再抽 去透热壁,进行等温等压混合△2S. △S=△1S+△2S CC) =(6.27×10-3+11.53)J·K-1 =11.54J·K-1 Cv,m(0)=Cv.m(N2)=5R/2 (6)过程是等温不等压混合,无现成公式.可设想中间隔板可左右滑动,因此过程首先达 到两边压力平衡,平衡时压力为1.5力°,然后再抽去隔板,此时为同种气体等温等压混合,所以 △S=△S左+△S右 =n)Rin5+n')Rn子 23

物理化学解题思路和方法 =1.41JK 由本题求算可知,计算的关键在于分析混合前后体系的状态是否改变,如改变又是如何变 的等.因此混合嫡是由各气体混合而产生的说法是不全面的 【例1.24】求下列化学反应的嫡变,并用嫡增加原理判断该反应在298K、p°下能否发 生?若升温到633K,反应能否发生? C2H50H(g,298K,p)+C,H(g,298K.b”)+HO(g,298K.b5) 已知反应的△.H(298K)=46.024 kJ.mol1 C2HOH(g) CH(g) HO(g) s(298K)/(J.K.mol-) 282.0 219.5 188.7 C.m(298 K)/(Jmol-1K) 73.26 43.56 33.58 解析△S体=(219.5+188.7-282.0)J小K-1mol1=126.2JK1mol1 △S=-H8K-6824小olrK=-154.4J-K-I.mol △S=△S体+△S环=-28.2J小K1mol1<0 所以据嫡增加原理,该反应在298K、力°下不能发生, 若升温到633K,应该用变温过程求算体系的△S和△H. 4,S(633K)=4S(298K)+ r63k△Cd=128.7JK1mo 298K 633K a,H633K)=△,H298K)+j30R△C.adT=44.7W·mo- △S环=-△其=4.710J·K1,mor1=-70.61J·K-1.m0 633 △S=(128.7-70.61)JK1·mol1=58.1J.K-1.m0l1>0 据嫡增加原理,反应在633K、力°下能发生. 【例1.2-5】将351K、p的1mol液体乙醇,在等温下始终对抗0.5p的恒外压蒸发为同 温的0.5p乙醇蒸气.请根据计算判断该过程是否为可逆过程.已知乙醇正常沸点为351K, 其AHm=39.53kmo1,液态密度p=0.7600gcm3,并假设蒸气为理想气体 解析判断过程是否可逆,可用熵函数,但必须是绝热封闭体系或孤立体系,本题不是绝 热,因此只能用孤立体系来判断,但此时特别注意不能仅仅以体系的熵变(△S体)来判断,而应 用△S体+△S环作为孤立体系熵变来判断是否为可逆过程.该方法是一个普遍适用的方法.另 外特别注意,该体系在始终态压力发生了改变且有相 1mol乙(g) 351K0.5p 变.而正常沸点是指压力为力下的液气间相变据以 上分析,先写出始、终状态,再设计可逆过程就可求算 △S体,△S环的求算关键在于把实际过程(不是设计的 过程)热效应Q求得,由于环境是一大热源,因此它 失、得有限量的热并不形响其温度值,可视过程为可 351KP0 逆,△S环=-Q/T(T为热源温度,即环境温度),示意 图1-10中:①为正常沸点下的可逆相变△15,②为可 图1.10 逆等温膨胀42S.①和②为设计的可逆过程
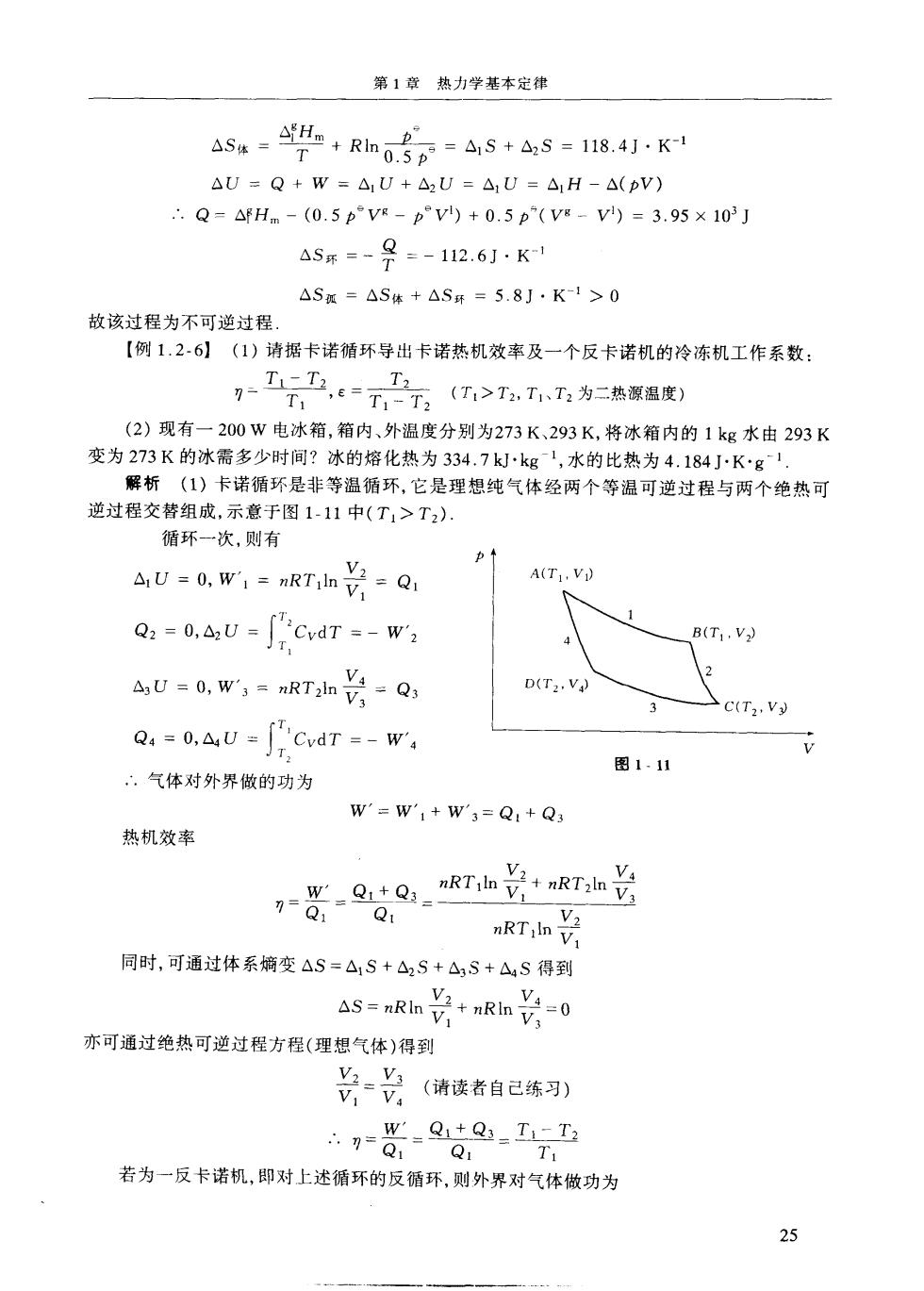
第1背热力学基本定律 △S-华+Rn0名6=45+aS=184:K △U=Q+w=△1U+△2U=△U=△1H-△(bV) .Q-△Hm-(0.5pv-p°Vl)+0.5p(Vg-V)=3.95×103J △5环=-号=-112.6J·K △S覆=△S体+△S环=5.8J·K-1>0 故该过程为不可逆过程 【例1.2-6】(1)请据卡诺循环导出卡诺热机效率及一个反卡诺机的冷冻机工作系数: 7-,e=:T>为三热 T (2)现有一200W电冰箱,箱内、外温度分别为273K、293K,将冰箱内的1kg水由293K 变为273K的冰需多少时间?冰的熔化热为334.7kkg',水的比热为4.184J小Kg1. 解析(1)卡诺循环是非等温循环,它是理想纯气体经两个等湿可逆过程与两个绝热可 逆过程交替组成,示意于图1-11中(T1>T2). 循环一次,则有 AU=0,w,=aRTh÷=Qi A(TL.V) Q:=0,4U=∫Cvdr=-w2 B(T:.V) aU=0,w,=nRTh长-Q D(T2.V) C(T2,V Q.=0.AU=["'CvdT =-W', .气体对外界做的功为 图1.11 W=w'1+w'3=Q1+Q3 热机效率 kTin 同时,可通过体系熵变△S=△1S+△2S+△,S+△S得到 AS=nRh÷+nRh÷=0 亦可通过绝热可逆过程方程(理想气体)得到 片光:(请读者自已练习列 9g-8g,2 若为一反卡诺机,即对上述循环的反循环,则外界对气体做功为

物理化学解题思路和方法 w=aRT.n兰+aRr,h号 ·气体从低温热源吸热 g=-Q=nRTh号 ·气体从高温热源吸热 g1=-Q=aRTh长 (该值为负,实际上为放热).在此循环中消耗外界功将热从低温热源传到了高温热源】 =0=r 12 (2)由e表达式 w. =293572273K[1000g×(293K-273K)×4.184J·K1·g 273K +1kg×(334.7×103J·kgl)] =6.15×103J 需时1=6,5x101=30.8s 200Js 【例1.2】请根据熵增加原理论证“在一个封闭体系的任一给定的平衡态附近总有这 样的态存在,从给定的平衡态出发不可能经绝热可逆过程到达此态”, 解析给定的平衡态附近某一态为非平衡态,从平衡态到非平衡态为不可逆过程,据熵增 加原理△S>0,若可用绝热可逆过程达到该态,则△S=0二者矛盾,故用绝热可逆过程达到该 态是不可能的 【例1.2.8】某-一密闭容器中隔板两边各盛子molO2(g)和子molN2(g),它们都是理想气 且温度压力都为T、力.抽出中间隔板,两气体则混合. (1)求混合嫡变及混合前后微观状态数之比. (2)若将混合后体系微观状态数作为1,问N2O2同时集中回到始态时的概率有多大? 解析(1)过程为等温等压混合过程 n0.1 j n ((.291 n(N) 据Boltzmann关系式 △s=kh8,8=et=2m 问题若容器中隔板两边皆为O2(g)或N2(g),请向△xS又如何? (2)01=e3.83×10”,概率非常之小,可视为根本不可能发生。 【例1.2-9】在一绝热箱中有两块用绝热板隔开的各为1m©l的银,温度分别为273K与 323K,在273~323K间银的等压摩尔热容为Cp.m=24.48JK-mol1.求: (1)抽去隔板后两块银达热平衡的熵变; 26