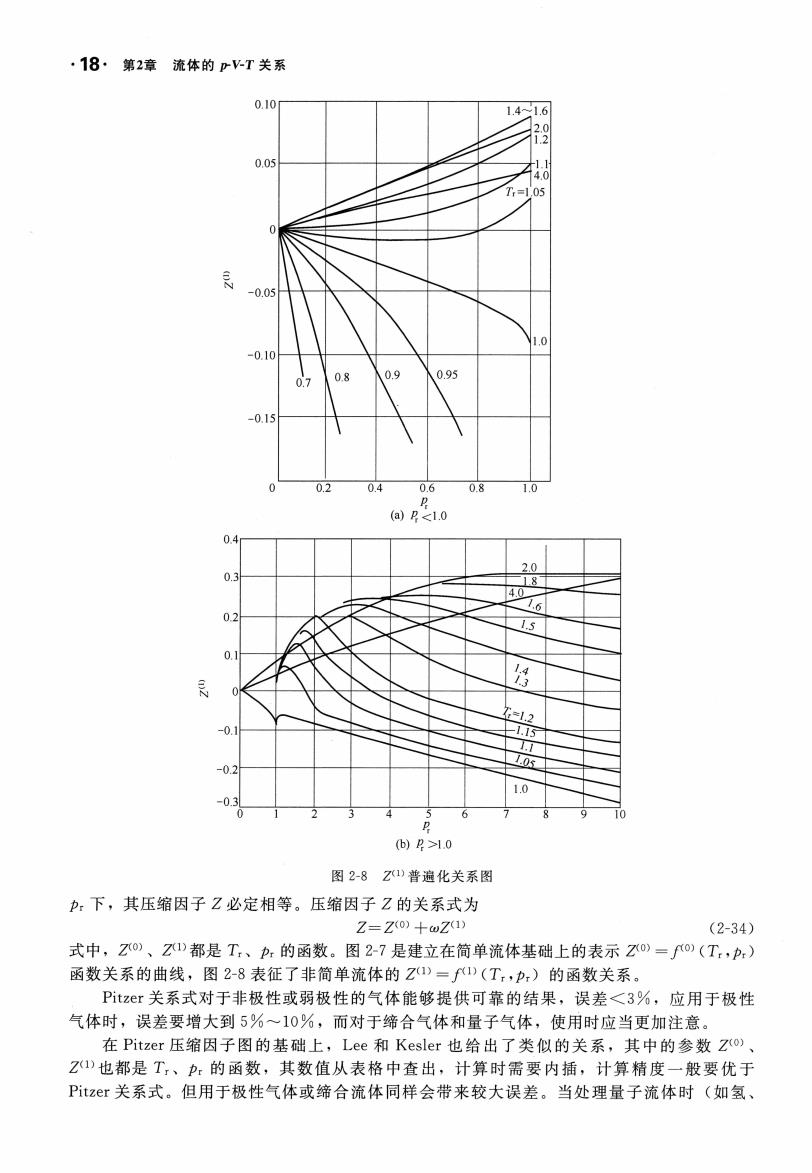
18·第2章流体的pT关系 141.6 0.8 02 04 0.6 0.8 a)R21.0 I.s 6 (b)2>10 图2-8Z1)普遍化关系图 力:下,其压缩因子Z必定相等。压缩因子Z的关系式为 Z=Z八0)+wZ八(1) (2-34) 式中,Z0)、Z都是T、p,的函数。图2-7是建立在简单流体基础上的表示Z0)=o(T,p) 函数关系的曲线,图2-8表征了非简单流体的Z1》一)(T,p)的函数关系。 Ptzr关系式对于非极性或弱极性的气体能够提供可靠的结果,误差<3%,应用于极性 气体时,误差要增大到5%~10%,而对于缔合气体和量子气体,使用时应当更加注意。 在Pitzer压缩因子图的基础上,Lee和Kesler也给出了类似的关系,其中的参数Zo) Z也都是T,、p:的函数,其数值从表格中查出,计算时需要内插,计算精度一般要优于 Pitzer关系式。但用于极性气体或缔合流体同样会带来较大误差。当处理量子流体时(如氢
.18. 章流体的 ~V-T 关系 N 0.2 AU AU MPHa< ( ) 21 AU 1.0 0.4 N (b) 月>1. Zo 普遍化关系图 下,其压缩因子 必定相等。压缩因子 的关系式为 z=z<o) ωzO ) (2-34) 式中 (l)都是 Pr 的函数 -7 是建立在简单流体基础上的表示 o) = 1'0) (汇,户r) 函数关系的曲线,图 2-8 表征了非简单流体的 Zω= j<ll (T ρr) 的函数关系。 er 关系式对于非极性或弱极性的气体能够提供可靠的结果,误差 <3% ,应 用于极性 气体时,误差要增大到 5%~ O% ,而对于缔合气体和量子气体,使用时应当更加注意 Pitzer 压缩因子图的基础上, Lee Kesl 也给出了类似的关系,其中的 参数 z< o) (l)也都是 Pr 的函数,其数值从表格中查出,计算时需要内插,计算精度一般要优于 Pitzer 关系式 但用于极性气体或缔合流体同样会带来较大误差 。当处 量子流体 时(如 氢

2.4普遍化状态方程·19 氢、氖),其对比性质的计算要特别处理,即使用与温度有关的“有效临界参数”进行计算。 【例2-4】利用Pitzer提出的普遍化压缩因子关联式,计算水在973.1K及2.5MPa下的 压缩因子,并与实验值Z-0.97进行比校。 解:在题给条件下,水的对比温度、对比压力分别为 T,=1.50, p:=1.13 水的偏心因子为w=0.345,由图2-7与图2-8分别查出 Z0)=0.898, Z八1)=0.08 根据式(2-34)得 Z=Z0)+mZ1)=0.898+0.345×0.08=0.926 本题计算结果比以Z。作为第三参数的压缩因子图求出的值为好。 2.4普遍化状态方程 所谓普遍化状态方程是指用对比参数T,、p、V,代替变量T、力、V,消去状态方程中反 映气体特性的常数,适用于任何气体的状态方程。 2.4.1普编化第二维里系数 将T=T,T、p=p,p:代入舍项维里方程式(2-10b)中得到 2-1+器-1+() (2-35) 式中,票是无量钢的,称作普遍化第二维里系数 由于对于指定的气体,B仅仅是温度的函数,与压力无关,Pitzer提出如下的关联式: -B +B() (2-36) 式中,Bo和B1)都只是对比温度的函数,表示为 Bo)=0.083-0.422/T.6 (2-37a) B=0.139-0.172/T (2-37b) 由于二阶舍项维里方程只适用于中、低压力下, 普遍化第二维里系数的使用必然也是有限制的。并且 普遍化维里系数使用 可以发现:式(2-34)和式(2-35)均将压缩因子Z表 示为(T,四)的函数。有人建议,两种方法的选 择可以根据其对比温度和对比压力参照图29。但这 普遍化压缩因子使用区 种选择依据没有经过严格的考核和证明。也有人研究 指出:当对比温度大于3以后,两种方法的计算结果 6 差异不大。随着对比温度降低,适用普遍化第二维里 系数的压力范围也将缩小。当对于温度到达0.7时, 图2-9普化关系式适用区域 适用压力应小于饱和蒸气压。 【例2-5】试计算正丁烷在510K和2.5MPa时的摩尔体积。已知实验值为1480.7cm㎡3·mol- (1)使用理想气体状态方程计算;(2)使用Pitzer三参数压缩因子图计算;(3)使用普遍
2.4 普遍化状态方程 .19. 氨、氛) ,其对比性质的计算要特别处理, 即使用 与温度有关的"有效临界参数"进行计算。 【例 2-4 利用 Pitzer 提出的普遍化压缩因子关联式, 算水在 973 .1K 2. MPa 下的 压缩因子,并与实验值 0.97 进行 较。 解:在题给条件下,水的对比 温度、对比压力分别为 Tr= l. 50 , Pr= l. 13 水的偏心因子为 ω=0 345 ,由图 2-7 与图 分别查出 Z <O) = O. 898 , Z(l) = O. 08 根据式 (2 34) Z=Z<O) ωZO l =0. 898 345 X O. 08=0. 926 本题计算结采比以 作为第三参数的 压缩因子图求出的值为好 2.4 普遍化状态方程 所谓普遍化状态方程是指用对比参数 ρr 代替变量 消去状态方程中反 映气体特性的常数,适用于任何气体的状态方程 2.4.1 普遍化第二维里系数 代入舍项维里方程式 (2 b) 中得到 (2-35) RT ~'RT / 式中, EZi是无量纲的,称作普遍化第二维里系数 RTc 由于对于指定的气体 仅仅是温度的函数,与压力无关, Pitzer 提出如下的关联式 Bpc _ ::_c <O) ωB (l RTc 式中 (O) (]) 都只是对比温度的函数,表示为 B(Ol = 0. 083 422 T~' 6 B(!) = 0.139 - 0.172/1;, 2 由于 舍项维里方程只适用于中、低压力下, 4 遍化第二维里系数的使用必然也是有 限制的 并且 3 2 3 Pr 可以发现:式 (2 34) 和式 (2 35) 均将压缩 示为 扣, 的函数。有人建议,两种方 的选 择可 以根据其对比温度和对 压力参照图 2-9 。但这 种选择依据没有 过严格的考核和证 也有人研 指出: 当对 比温度大 ,两种方法的计算结果 差异不大 随着对比温度降低,适用普遍化第 维里 系数的压力范围也将缩小 当对于温度到达 时, 适用压力应小于饱和蒸气压。 -9 普遍化关系式适用区域 ( 2-36) (2-37a) (2-37b) 8 【例 -5 试计算正丁;比在 510K 孔1P 时的 尔体和、 已知 实验值 1480 cm • mo] (1)使用 理想气体状态 方程计算 (2) 使用 Pitzer 三参数压缩 因子围计算 (3) 使用普遍

·20·第2章流体的PT关系 化第二维里系数计算。 解: (1)使用理想气体状态方程: v_RT_8.314X510-1696.1cm·mol1 2.5 (2)首先从附录三中查出其临界参数:T。=425.12K,九=3.796MPa,w=0.199,乙。=0.274 工=2=120,A-286=0.650 510 由图2-7和图2-8查得 Z八0)=0.865. Z1)=0.038 Z=Z0)+uZ1)=0.865+0.199×0.038=0.873 V=ZRT_0.873×8314×510=1480.7cm,mol- 2.5 (3)由式(2-37a)和式(2-37b)计算得 Bo)=0.083-0.422/(1.200)1.6=-0.232 B1)=0.139-0.172/(1.200)42=0.059 由式(2-36)得 0=Bo+Bm=-0.232+0.199×0.059=-0.20 由式(2-35)得 Z=1+(-020)×是器=a879 V-2RT_0.879×8314X510=1489.1m·mol1 25 结果表明,对于本题使用两种对比态法的计算偏差在1%以内。 【例2-6】试计算0.4536kmol甲烷贮存于2f3(0.0566m3)的钢瓶内,当温度为122℉ (323.15K)时钢瓶承受的压力。已知实验值为18.75×105Pa。 (I)使用理想气体状态方程计算;(2)使用Redlich-Kwong方程计算;(3)使用对比态 原理进行计算。 解: (1)根据理想气体状态方程: (2)首先从附录三中查出甲烷的临界参数为:T。=190.56K,p。=4.599MPa,m=0.011。 将Te、p:值代入式(2-14a)和式(2-14b)得 a=0.42748X(83142×190.56》2=3.207Pa·m5·Ka5·mol- 4.599×10° 6=0.08664×8.314X190.56=2.9847×10-5m·mol-1 4.599X105 代入式(2-13)得 8.314X323.15 3.2207 ♪=0.0566/453.6-2.9847×10-(323.15)43×(0.0566/453.6)×(0.0566/453.6+2.9847X10 =19.01×106Pa (3)由于此题压力比较高,易选用压缩因子图进行计算;但此时缺少压力,无法计算对 比压力p,必须进行试差计算。 1
.20. 章流体的 p- V-T 关系 化第二维里系数计算。 解: (1)使用理想气体状态方程: RT 8. 314 X 510 _ n^n _ ? v= 一一= ~. V4^~ '_' V4V = 1696. 1cm3 • mol- 1 P 2. 5 (2) 首先从附录三中查出其临界参数: Tc =425. 12K =3.796肌1P ω=0.199 Zc=0. 274 T 51o 一一一一 1. 200 , 425. 12 2. 5 =一一一 =0 659 3. 796 由图 2-7 和图 查得 Z<O) =0. 865 , ZOl = 0. 038 <O) ωZO l = 0. 865 + 0. 199 X 0. 038 =0. 873 ZRT O. 873 X 8. 314 X510 v= 一一一 _V '~ 4~ "V 480.7cm mol- 1 ρ2. 5 (3) 由式 (2-37a) 和式 (2-37b) 算得 B<Ol =0. 83 0.422 1. 200) 1. 6= 232 B(l) = 0. 139 17 1. 200 )4. 2=0. 059 由式 (2-36) Bp::_c =Bn{< 川门0) +ωB(l ) =一 232 +0 199 X O. 059= 220 RTc 由式 (2 35) O. 659 Z=l+( 0.220) 一一一一 =0 879 1. 200 ZRT O. 879 X8. 314 X 510 一一一 v . V I V /"::- .L -r / " V.LV = 1489. l cm3 • mol- 1 2. 5 结采表明 ,对于本题使用两种对 比态法的计 算偏差 以内 【例 2-6 试计算 0.4536kmol 比贮存 2ft ( 0. 0566m3 )的钢瓶 ,当温度为 22 (323. 15K) 时钢瓶承受的压力 已知实验值为 75X 10 Pa (1)使用理想气体状态方程计算 (2) 使用 dlich K wong 方程计算; (3) 使用对 比态 原理进行计算 解: (1)根据理想气体状态方程 R T 8. 314 X 323.15 ^_ _^ . . _^" ,= (() ()r:;('.('./ 1. 53 X 100 Pa (2) 首先从附录三中查出甲 的临界参数为: Tc= 190. 56K , 99MP =0 011 值代入 4a) 和式 (2 14b 0. 42748 X (8.314) 2 X (1 90. 56) 2. 5 V. V' V^4^ ./ ~"'4 VV VV/ 3. 2207Pa . m6 • KO. 5 . mol- 2 4. 599 X 106 O. 08664 X 8. 314X 190. 56 b= v . VVV~ ~ '::'^ v ~" . vv = 2. 9847 X 10- 5 m3 • mol-1 4. 599 X 100 代入式 (2 3) &314 X 323. 15 3. 2207 0. 0566/ 453. 6- 2. 9847 X lO- 5 (323.1 X (0.0566/453.6) X (0.0566/ 453.6+2. 9847 X 10- 5) = 19. Ol X 106Pa (3) 由于此题压 力比较高,易选用压缩因子图进行计算;但此时缺少压力户,无法计算对 比压力扣,必须进行试差计 算。 ZRT 23 .1 ε 一一一 ,V: V^4_ '^'^' . _ v: 4^V, = 21. 53 X 106 Z V (0. 0566/ 453. 6)

2.4普遍化状态方程·21· 又p=p:p,=4.599X106p,故 p,=4.682或Z-0.2137p, 可以省先根位Z=1,则根据T一瓷号-1.695和-46的,麦图27卡图28得到 Z0、Z)。使用式(2-34)进行计算,得到一个新的Z,由这个新Z值得到一个新p,值。这 样反复计算,直到两步的Z值没有明显变化为止。最后可以得到Z=0.890,p,=4.14。则 RT_8.314X323.15×0.890=10,16×100Pa p=V (0.0566/453.6) 结果表明:三参数压缩因子图及RK方程均能给出比较好的结果,而理想气体状态方程的 计算误差则高达14.6%。 【例2-7】将20×105Pa、478.6K的NH3,由3m3压缩至0.15m3。若终温为450.2K, 压力是多少?已知NHa的格界参数及偏心因子分别为:T。=405.65K,p=112.78×105Pa, V.=72.6×10-5m3·mol-1,w=0.252。 解:始态时 -高-18 20×105 m-112.78X10=0.177 由于压力较低,可以使用普遍化第二维里系数计算。由式(2-37a)和式(237b)得 Bo)=0.083-0.422/T6=0.083-0.422/(1.18)1.6=-0.241 B)=0.139-0.172/T2=0.139-0.172/(1.18)2=0.053 由式(2-35)和式(2-36)得 Z=1+0=1+[Bo+wB门(2)=1+(-0.241+0.250×0.053)×.g=0.966 17 终态时可以采用RK方程进行计算。将T、p。值代入式(2-14a)和式(2-14b)得 006805.65=25909×10-m·mo-1 代入式(2-13)得 8683 =18.42×10Pa 2.4.2普遍化立方型状态方程 将2.2.2节中讨论的立方型状态方程中的p、V、T参数,在对比态原理的基础上,改换 成对比态参数T:、P、V:的形式,并消去方程中的特定常数项,则可得到相应的普遍化立方 型状态方程。 如van der Waals方程为 (2-11) 利用等温线在临界点上的斜率、曲率均为零的特征,即
2.4 普遍化状态方程 .21 . Pr =4 599X 10 户,故 Pr=4. 68Z Z=0. 2137Pr 323. 15 可以首先假设 则根据 一一一一 1. 695 ρr = .6 查图 2-7 和图 -8 得到 190.56 (O) (l)。 使用式 (2 -34 )进行计算,得到 个新的 Z. 由这个新 值得到 个新 pr 样反复计算,直到两步的 值没有明显变化为止 最后可以 =O 890. pr =4 PZRT 8. 314 × 323. 15× 0.89Oa - -二 .1 Pa V (0. 0566/ 453.6 ) 结果表明:三参数压缩因子图及 RK 方程均能给出比较好的结采,而理想气体状态方程的 计算误差则高达 【例 -7 20 X 10 Pa 47 .6K NH 压缩至 若终温为 450 .2K. 压力是多少 已知 NH 的临界参数及偏心因子分别为 =405 65K.ρ 11 . 78 X 105Pa. V c = 72. 6 X 10- 5 m3 • mol- 1 .ω=0.252 0 :始态时 T 478.6 T r =;" = '~ ~~~ =1. 8 T c 405.65 P r= lL =2OX O. 177 112.78 X 10" 压力较低,可以使用普遍化第 维里系数计算 由式 (2 37a) 和式 (2- 37 B(O) =0. 083 422 . 6 = O. 083 - 0. 422/ (1. 18) 1. 6 = -0. 241 B (] ) =0 .1 39 o. 172 ~. 2 =0.139 - 0.172 / (1 .18) 4. 2 =0. 053 由式 (2 -35 )和式 (2-36) Z=l+RT 旦主 ~'L~ +[B (O) 'WωB~ (1) ] _j \T(生)rJ = 1 + " (-0.24 '~.~'1 +0.250 '~ ~~"~X 0. 053) ~~~/'' 旦旦1. 8 2=0 .966 (n V) 2OX 105 X 3 一一一一 r. '" ,. , ~ f""\ ." i • n;;- = 156 1mol ZRT 0. 966X8 . 终态时可以采用 RK 方程进行计算 值代入式 (2 4a) 和式 (2 b) O. 42748 X (8. 314) 2 X (405.65) 2.5 α~. .~. .,//, :-::-. ':: :~ ~~.V~' vV/ =8. 683Pa ' m6 • KO. 5 • mol-2 11. 278 X 106 O. 08664 X 8. 314 X 405. 65 , .VV ' v~=2 . 5909 X 10-5 m3 • mol- 1 11. 278 X 10" 代入式( 3) 8. 314 X 450. 2 8. 683 = 0.15 / 1561 -2. 5909 X 10- 5 (450. 2) 0. 5 X (0.15/ 156 1) X (0.15 / 1561 +2. 5909 X 10- 5) = 18. 42X 106 Pa 2. 4. 2 普遍化立方型状态方程 2. 节中讨论的立方型状态方程中的户、 参数,在对比态原理的基础上,改换 成对比态参数 的形式,并消 去方程 中的特定常数项,则可得到相应的普遍化立方 型状态方程 va der Waals 程为 RT a P= V - b V 2 利用 等温线在 临界点上的斜率、曲 均为 的特征,即 (2-11 )

·22·第2章流体的pT关系 (2+将-0 (2-38a) 器),-26贵0 (2-38b) 联立式(2-38a)和式(2-38b)得 Ve=36 (2-39a) T:=品×旅 (2-39b) 将式(2-39a)和式(2-39b)代入式(2-11)中得 p.-270 (2-39c) 0x号碳g (239d 277X36 3 (2-39e) 代入式(2-39a)得 (2-40a) 将式(2-40a)代入式(2-39b)中整理得 a=27R37 (2-40b) 64Pe 将T=T,T、p=p,pe、V=V,V:及式(2-40a)、式(2-40b)代入式(2-11)并整理可得 (+2)3v,-1)=8T (2-41) 即为普遍化van der Waals方程 利用同样的方法可得到普遍化RK方程。 37T: 92. p,-V,-3-T5V,(V,+30) (2-42) 其中:2=0.427480,26-0.086640 【例2-8】将以下形式表示的RK方程,改成普遍化的形式 h-壁 式中,B=R:合-Ria和b为RK参数. 解:将式(2-14a)及式(2-14b)代入题给的B及A/B的表达式中,并令T=T,T,化简 后得到 B-pT'B-ChT:5 分别将B、A/B值代入式(2-17)和式(2-17b)中,并令式(2-17b)中p=pp,得到RK方 程另一个善遍化的形式为
(PT2G C2-38a) V )T 一」一← (V -b) =0 (主主) éJVZ J T =JEL CV 一些 =0 c -b)3 V : .22. 流体的 -T 关系 C2-38b) V c=3b C2-39a) 俨=立 c 27 " bR 联立式 38a) 和式 C2 38b) C2-39b) 将式 C2-39a) 和式 C2-39b) 代人式 2-11) C2-39c) C2-39d) G c= 一 c 27bz .~ 主二_ , 2 7 c Pcvc ::. X 3b 27b< Vc = - 3RTc c - C2-3ge) R-8 代入式 C2-39a) C2-40a) C2-40b) 中整理得 27R ~ 一一一一一一一一 64pc T=T PrPc V=VrV 及式 C2-40a) 、式 2-4 0b) 代入式 2- 11 )并整理可得 将式 (2 -4 0a) 代入式 (2 -39 b) (Pr+ 告) 肌一 1) =8Tr (2-41 ) 即为普遍化 van der Waa 方程 利用同样的方法可得到普遍化 RK 方程 r - 3Tr 一一一旦 b . 5V r CVr +3Qb) C 2-42) 其中 0.427480 = 0. 086640 将以下形式表示的 RK 方程,改成普遍化的形式 =~ ~(Á一‘ì 1-h B \l+hJ 【例 2-8 b A 式中, RT' B bRl -iTτ ;α RK 参数。 匕简 寻到 RK 及式 (2 14b) 代入题给的 的表达式中, 并令 T r T c , Aοa Bοb T;' 5 中,并令式 -1 Bοb - P c Tr ' 分别将 位代入式 C2 7a) 和式 2-17b) 程另一个普遍化的形式为 将式 (2 14a) 后得到