
2.2流体的状态方程·13 其中, y-品 (2-23) 该方程是由Carnahan-Starling提出的,是通过修改van der Waals方程的斥力项实现的: 它可以更好地表达中密度下斥力对流体性质的影响,是应用非常广泛的一种硬球型方程。很明 显,该方程的斥力项不是立方型的,计算更加复杂。 (2)1 shikawa et al方程(1980年) p=RT(2V+6) (2V-b) -To V(V+6) (2-24) 该方程修正了立方型状态方程的斥力项,并将该斥力项与RK方程的引力项相结合。 由于硬球型状态方程能处理在石油炼制和天然气工业中所遇到的大部分混合物的大小、形 状和势能分布不同的混合物,因此硬球型状态方程是一种新的且很有开发前途的方程。目前这 方面工作仍在继续。 2.2.5多参数状态方程 与简单的状态方程相比,多参数状态方程可以在更宽的T、范围内准确地描述不同物系 的pVT关系;但其缺点是方程形式复杂,计算难度和工作量都较大。 (1)Benedict-Webb-Rubin方程(1940年) 该方程属于维里型方程,简称BW℉方程,在计算和关联轻烃及其混合物的液体和气体热 力学性质时极有价值。其表达式为: p=RTp+(Bo RT-Ao-)+(bRT-a)p+aap+zp(1+Yp)exp(-Yo2)(2-25) 式中,p为密度;Aa、Bo、Co、a、b、c、a和y等8个常数由纯物质的pV-T数据和蒸气压 数据确定。目前已具有参数的物质有三四十个,其中绝大多数是烃类。 在烃类热力学性质计算中,BWR方程计算的平均误差为0.3%左右,但该方程不能用于 含水体系。 以提高BWR方程在低温区域的计算精度为目的,Starling等人提出了Il个常数的Star 1ig式(或称BWRS式)。该方程的应用范围更广,对比温度可以低到O.3,对轻烃气体 CO2、H2S和N2的广度性质计算,精度较高。总的说,BWRS式更准确些,也更复杂些。 (2)Martin-Hou方程(1955年) 该方程是1955年Martin教授和我国学者侯虞钧提出的,简称MH方程(后又称为MH5 型方程)。为了提高该方程在高密度区的精确度,Martin于1959年对该方程进一步改进,1981年 侯虞钧教授等又将该方程的适用范围扩展到液相区,改进后的方程称为MH81型方程。 MH方程的通式为: 2- (2-26) 式中f(T)=A,+B,T+Cexp(-5.475T/T)(2≤i≤5) f1(T)=RT(i=1) 式中,A,、B,、C、b皆为方程的常数,可从纯物质临界参数及饱和蒸气压曲线上的一点数据 求得。其中,MH-55方程中,常数B:=C=A5=C6=0,MH-81型方程中,常数C4=A C=0 MH-81型状态方程能同时用于汽、液两相,方程准确度高,适用范围广,能用于包括非 极性至强极性的物质(如NH3、H2O),对量子气体H2、He等也可应用,在合成氨等工程设 计中得到广泛使用
2. 2 流体的状态方程 .13. b 其中 y= ( 2-2 3 ) J 4V 该方程是由 Carn Starl ng 提出的,是通过 der aa ls 方程的斥力 项实现 它可以更好地表达中密度下斥力对流体性质的影响 是应用非 广泛的 种硬球型方程。很 显,该方程 斥力项不是立方型的,计算更 复杂。 (2) Ishikawa et al 方程 (1 98 T(2V b) V(2V- b) T ü.5V(V+ b) (2-24) 该方程修正了立方型状态方程的斥力项,并将该斥力项与 RK 方程的引力项相结合。 于硬球型状态方程能处理在石油炼制和天然气工业中所遇到的大部分混合物的大小、形 状和势能分布不同的 昆合物,因此硬球型状态方程是 新的且很有开发前途的方程 目前这 方面工作仍在继续 2.2.5 多参数状态方程 与简单的状态方程相比 多参数状态方程可以在更宽 范围内 准确地描述不同物 关系 但其缺点是方程形式复杂,计算难度和工作 都较大 (1) Benedict-Webb-Rubin 方程 (1 940 年) 该方程属于维里型方程,简称 WR 方程,在计 和关联轻短及其混合物的液体和气体热 力学性质时极有价值 其表达式为 (n n 'T' ^ Co \ RTp+ ~ BoRT- A o - ~ 2 + (bRT α)ρ3+ (1 听)叫 yp (μ5 ) 式中, 为密度 数由 纯物质的 p- 数据和蒸气压 数据确定 目前己具有参数 物质有 四十个,其中绝大 数是短类 在;怪类热力 性质计 中, BWR 方程计算的平均误差 左右, 但该方程不能用于 水体系 以提 BWR 方程在低温区域的计算精度为目的, St in 人提出了 11 常数的 li ng 式(或称 BWRS 式) 。该 方程的应用范围 更广 ,对比 温度 可以低到 ,对 轻;怪气 体, 的广度性质计 ,精度较高 。总的说, BWRS 更准确些,也更复杂些 ( 2) Martin- 方程 (1 955 年) 该方程是 19 55 rtin 授和我国学者侯虞钧提出 的,简称 MH 方程(后又称为 55 型方程)。为了提高该方程在高密度区 精确度, rtin 959 该方程 步改进 981 钧教授 将该方 适用范围扩展到液 改进后 称为 型方程 MH 方程 通式为 户交 T) (V - h )i T) exp( -5 75 )(2 ζ5 ! , (T) = RT (i = l) (2-26 ) 、旦、 皆为方程 常数 可从纯物质临界 饱和蒸气 线上的 点数据 求得 其中 -55 方程 中,常 =C4 = A 5 =C5 =0 , MH-8 型方程 中, 常数 =A5 = MH- 型状 方程能同时用 于汽 液两相 程准确度 高,适用范 围广,能用 于包括非 极性 强极性的物质( Ü),对 子气 也可 用,在合成氨等工程 计中 得到广泛使用

,14·第2章流体的pT关系 2.3对比态原理及其应用 2.3.1对比态原理 对比态原理(对应状态原理)认为,在相同的对比态下,所有的物质表现出相同的性质。 定义: T=, 式中,T、p、V、A分别称为对比温度、对比压力、对比摩尔体积和对比密度。 对比态原理最初提出是经验的,但后来也有人从理论上进行分析,例如从统计热力学指出 它的合理性,也可以从微观的角度进行讨论,用微观参数代替T。、p、V。确定对比态。用微 观参数后,对比态法的应用范围可扩大到传递性质,还可以应用于混合物。 将对比变量的定义式代入van der Waals方程得到 (p,+3/)(3V,-1)=8T (2-27) 该方程就是van der Waals提出的简单对比态原理。 简单对比态原理就是两参数对比态原理,表述为:对于不同的流体,当具有相同的对比温 度和对比压力时,则具有大致相同的压缩因子,并且其偏离理想气体的程度相同。 这种简单对比态原理对应简单流体(如氩、氢、氙)是非常准确的。这就是二参数压缩因 子图的依据,至今几乎所有的物理化学教材中都附有这张图。 van der Waals提出的简单对比态原理表明,对不同的气体,若其p,和T,相同,则V,也 必相同。 又因为 (2-28) 由简单对比态原理知:只有在各种气体的临界压缩因子Z。相等的条件下,才能严格成立 而实际上,大部分物质的临界压缩因子Z。在0.2~0.3范围内变动,并不是一个常数。可见, 范德华提出的简单对比态原理只是一个近似的关系,只适用于球形非极性的简单分子。虽然在 20世纪60年代以前,在化工热力学及其他热力学计算中得到广泛的使用,但精度、准确性 广泛性都有限,拓宽对比态原理的应用范围和提高计算精度的有效方法是在简单对比态原理 (二参数对比态原理)的关系式中引入第三参数。 2.3.2三参数对比态原理 (1)以Z。为第三参数的对比态原理 从式(228)中可以看出,可以引入物质的临界压缩因子Z。作为第三参数。1955年 Lydersen等人以Z:作为第三参数,将压缩因子表示为 Z=f(T:.p.Ze) (2-29) 即认为Z。相等的真实气体,如果两个对比变量相等,则第三个对比变量必相等。Lydersen等 人根据包括烃、醇、醚、酯、硫醇、有机卤化物、部分无机物和水在内的82种不同液体与气 体的pV-T性质和临界性质数据,作出了Z。在0.23~0.30范围内的四张压缩因子图,不仅 可用于气相,还可用于液相。其中Z。=0.27的图应用最广。其相应的计算压缩因子Z为 Z=Z+D(Z.-0.27) (2-30) 式中Z为所求的流体的压缩因子,Z为Z=0.27时流体的压缩因子,D为乙≠0.27时的校正系数 相应的图为图2-4和图2-5
.14. 章流体的 ]r V-T 关系 2.3 对比态原理及其应用 2.3.1 对比态原理 对比态原理(对应状态原理)认为,在相同的对比态下,所有的物质表现出相同的性质 T tJ. V 1 定义 ,= ρ= _1二 ,= →=一 T c ' c r VC ρr 式中 、户 ρr 分别称为对比温度、对比压力、对比摩尔体积和对比密度 对比态原理最初提出是经验的,但后来也有人从理论上进行分析,例如从统计热力学指出 它的合理性,也可以从微观的角度进行讨论,用微观参数代替 确定对比态 用微 观参数后,对比态法的应用范围可扩大到传递性质,还可以应用于混合物 将对比变量的定义式代入 van der Waa 方程得到 (Pr+3 / V ;) (3Vr - 1) =8T r (2-27) 该方程就是 van der Waa 提出的简单对比态原理 简单对比态原理就是两参数对比态原理,表述为:对于不同的流体,当具有相同的对比温 度和对比压力时,则具有大致相同的压缩因子,并且其偏离理想气体的程度相同。 这种简单对比态原理对应简单流体(如氧、氮、缸)是非常准确的。这就是 参数压缩因 子图的依据,至今几乎所有的物理化学教材中都附有这张图 van der Waals 提出的简单对比态原理表明,对不同的 体,若其 相同,则 必相同 又因为 Z=EIf 主主 0'r=Z rV (2 -28) RT RTc " T r - C T r 由简单对比态原理知:只有在各种 体的临界压缩因子 相等的条件下,才能严格成立。 而实际上,大部分物质的临界压缩因子 O. 2~0. 范围内变动,并不是一个常数。可见, 范德华提出的简单对比态原理只是一个近似的关系,只适用于球形非极性的简单分子 虽然在 20 世纪 60 年代以前,在化工热力学及其他热力学计算中得到广泛的使用,但精度、准确性、 广泛性都有限,拓宽对比态原理的应用范围和提高计算精度的有效方法是在简单对比态原理 参数对比态原理)的关系式中引入第三参 2.3. 2 三参数对比态原理 (1) Zc 为第三 参数 的对比 原理 从式 (2 28 )中可以看出,可以引人物质的临界压缩因子 作为第三参数 1955 dersen 等人以 作为第 参数,将压缩因子表示为 Z= f(T "Z ) (2-29) 即认为 相等的真实气体,如果两个对比变 相等,则第 个对比变 必相等 Ly dersen 人根据包括腔、醇、醋、醋、硫醇、有机卤化物、部分无机物和水在内的 82 种不同液体与 体的户 性质和临界性质数据,作出了 23~0. 30 泡围内的四张压缩因子图,不仅 可用于气相,还可用于液相 。其 c= 27 的图应用最广 其相应的计算压缩因子 Z' =Z+D(Zc -0.27) (2-30) 式中 Z' 为所求的流体的压缩因子 ;Z c= 0.27 时流体的压缩因子 ;D 0.27 时的校正系数 相应的图为图 2-4 和图 2-5
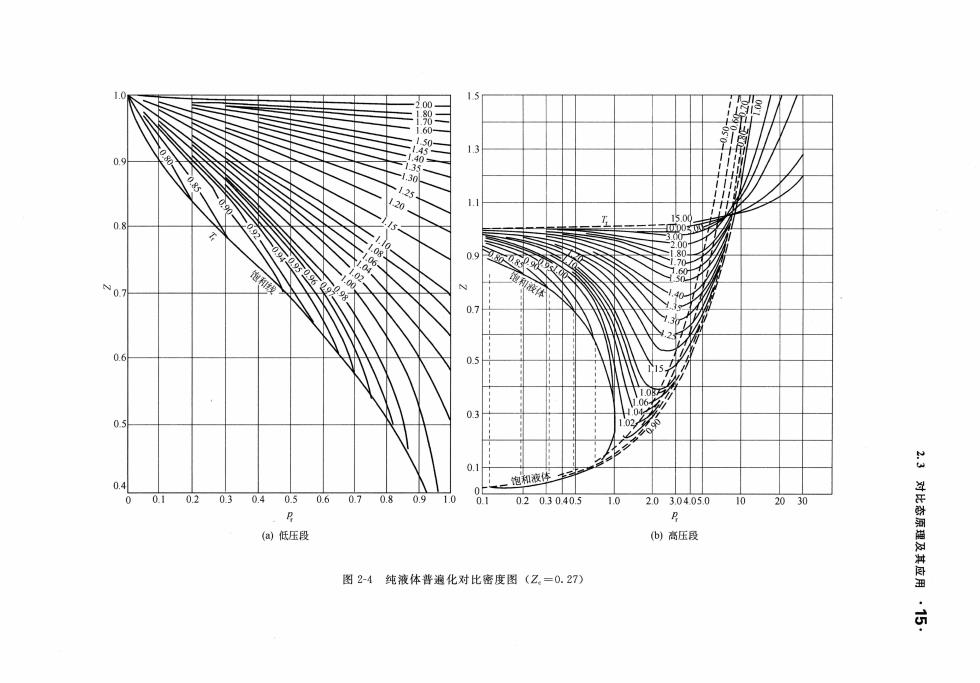
0.1 01 0.2 0.3 0.4 0.5 0.6 0.7 0.8 09 0203040.5 1.020304050 10 (@)低压段 b)高压段 图2-4纯液体普遍化对比密度图(Z。=0.27)
N-u 1.5 0.9 队心 0.7 13 0.5 0.3 3.04.05.0 10 20 30 (b) 高压段 0.5 0.1 0.2 0.3 0.4 0.5 10 2.0 R (a) 低压段 0. 1 0.2 0.3 .Jo m -4 纯液体普遍化对比密度图 (2 =0.27)
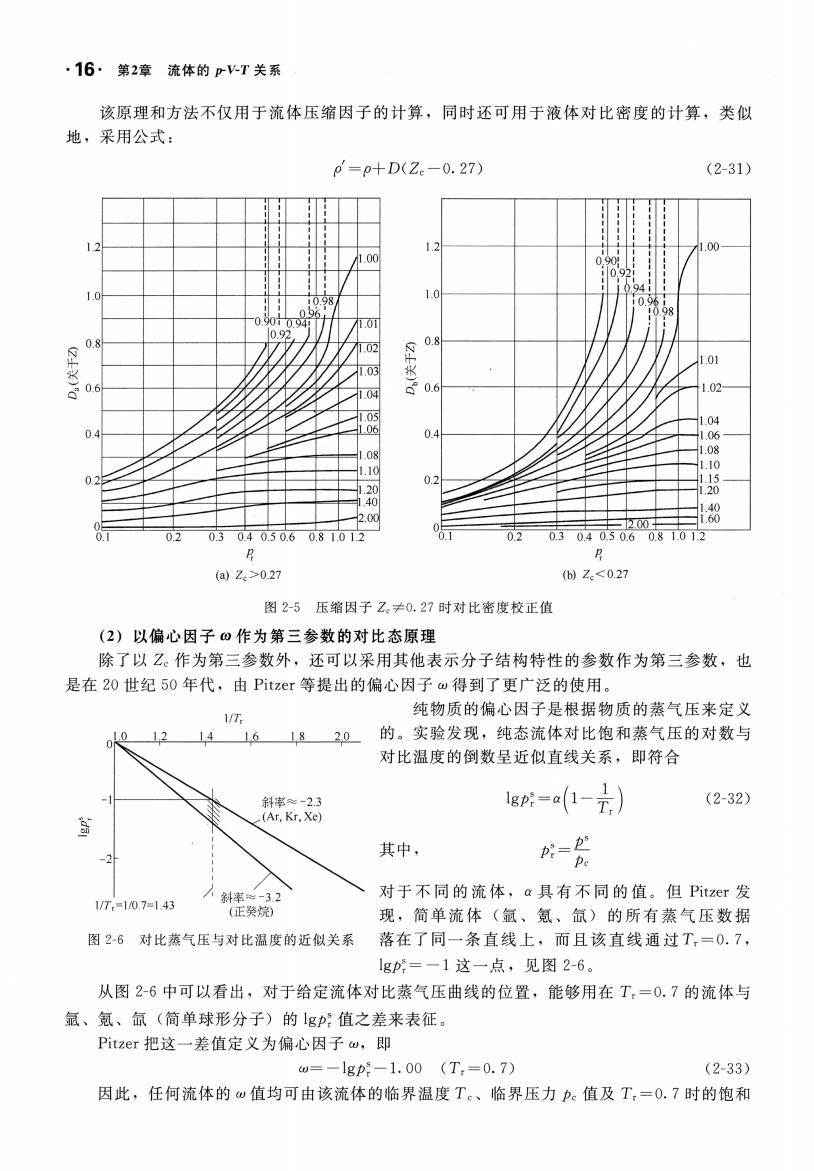
·16·第2章流体的pV-T关系 该原理和方法不仅用于流体压缩因子的计算,同时还可用于液体对比密度的计算,类似 地,采用公式: p'=p+D(Z-0.27) (2-31) .00 10 1.01 02 0 03 0 04 1.02 04 1.08 01 2.00 迈.00 8 02 0.3040.50.60.81.012 1 0.2 0.30.40.50.6081.012 P (a)Z.>027 ()Z<027 图2-5压缩因子Z。≠0.27时对比密度校正值 (2)以偏心因子ω作为第三参数的对比态原理 除了以Z。作为第三参数外,还可以采用其他表示分子结构特性的参数作为第三参数,也 是在20世纪50年代,由Pitzer等提出的偏心因子w得到了更广泛的使用。 1/T 纯物质的偏心因子是根据物质的蒸气压来定义 0 1214161820 的。实验发现,纯态流体对比饱和蒸气压的对数与 对比温度的倒数呈近似直线关系,即符合 斜率≈-2.3 _(Ar.Kr.Xe) 1g=a1-元)) (2-32) 其中, 好- 1VT=107143 32 对于不同的流体,a具有不同的值。但Pitzer发 现,简单流体(氩、氪、氙)的所有蒸气压数据 图26对比蒸气压与对比温度的近似关系 落在了同一条直线上,而且该直线通过T,=0.7, 1gp:=一1这一点,见图2-6。 从图2-6中可以看出,对于给定流体对比蒸气压曲线的位置,能够用在T:=0.7的流体与 氩、氪、氙(简单球形分子)的g:值之差来表征。 Pitzer把这一差值定义为偏心因子w,即 =-1gp:-1.00(T:=0.7) (2-33) 因此,任何流体的w值均可由该流体的临界温度T。、临界压力p。值及T,=O.7时的饱和
.16. 章流体的 该原理和方法不仅用于流体压缩因子的计算,同时还可用于液体对比密度的计算,类似 地,采用公式 +D(Z 27) 1.2 , 1 , ' 1 ' , 1 , ' 1 , ' 111 00 , 1 , I I ! 11: 1/ ' 1 ' b0t9 / 0900910,94j ! T!7 / 1.01 / Y/ γ/ γ 1.02 ~ V V/. ;少 v 1.03 JØ ~ ~ 以二 V / 1.04 /叮w v v - 1.05 1.06 /一V/ v }::: 二, 1.08 /乒:r:.- / J 1 10 卢-.J.- •- 1.20 -卢- 1.40 -•- 1- 2.00 一一 一- 1.0 N' 0.8 ft., 割〈 0.4 0.2 0. 1 0.2 0.3 0.4 0.5 0.6 0.8 1.0 1.2 R (a) Zc > 0.27 (2-3 1) 1.2 1.0 N' 0.8 ft., 利〈 Q 0.6 1.02 0.4 压缩因子 27 时对 比密度校正值 以偏心因子 作为第三参数 的对比态原理 除了以 作为第 三参数外,还可以采用其 表示分子结构特性的参数作为第三参数,也 是在 20 世纪 50 年代,由 Pitze 等提出的偏 因子 得到了更广泛的使用。 纯物质的偏心因子是根据物质的蒸气压来定义 1fT, l 4 1.6 1. 8 20 的。实验发现,纯态流体对比饱和蒸气压的对数与 对比温度的倒数呈近似直线关系,即符合 对于不同的流体, 具有不同的值 Pitz 现,简单流体(氧、氮、{lit)的所有蒸气压数据 对比蒸气压与对比温度的近似关系 落在了同一条直线上,而且该直线通过 Tr=O 7, 9p = 点,见图 从图 2-6 中可以看出,对于给定流体对比蒸气压曲线的位置,能够用在 =0 的流体与 氧、氮、{lit(简单球形分子)的 9p 值之差来表征 Pitzer 把这 差值定义为偏心因子 9J月一 1. 00 (Tr =0.7) (2-33) 因此,任何流体的 值均可由该流体的临界温度 、临界压力在值及 =0.7 时的饱和 -2 /斗 斜率 "" - 3.2 (正突烧 IfT,= lfO 7= 1.43 9p~= α( 去) (2-32) 其中, - rρc
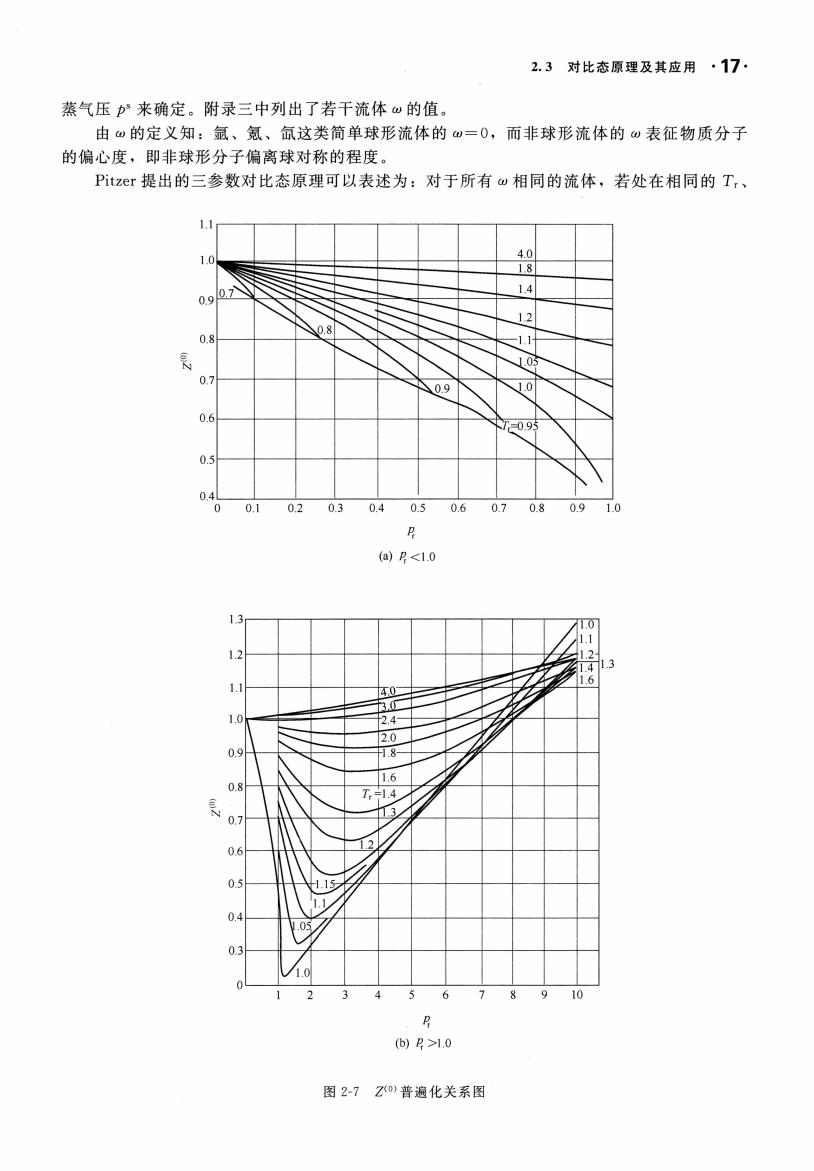
2.3对比态原理及其应用·17 蒸气压p来确定。附录三中列出了若干流体仙的值。 由“的定义知:氩、氯、氙这类简单球形流体的仙=0,而非球形流体的m表征物质分子 的偏心度,即非球形分子偏离球对称的程度。 Ptzr提出的三参数对比态原理可以表述为:对于所有w相同的流体,若处在相同的T:、 0.8 01 02 03040.50607 08 0.9 (a)R<10 04 6 图27Z普遍化关系图
2.3 对比态原理及其应用 .17. 蒸气压 来确定。附录三中列出了若干流体 的值。 的定义知:氧、氮、缸这类简单球形流体的 ω=0 ,而非球形流体的 表征物质分子 的偏心度,即非球形分子偏离球对称的程度 Pitz er 出的 三参数对 比态原理可以表述为:对于所有 相同的流体,若处在相同的 1.1 O N 0.4 o 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 R (a) Ii < 1.0 1.3 4 1.0 1.1 1.2 百乡 1.4 吨。 '7ß. 1.6 -二-_. 写' 眨之」 2.0 已\ 叭队 1. 1.6 8 ~ r ? ~\ Ì'- ilv V{O 3 1.2 l 0.9 0.8 0 N 0.7 0.6 0.5 0.4 0.3 2 3 4 5 6 7 8 9 10 (b) Ii >1.0 2-7 普遍化关系图