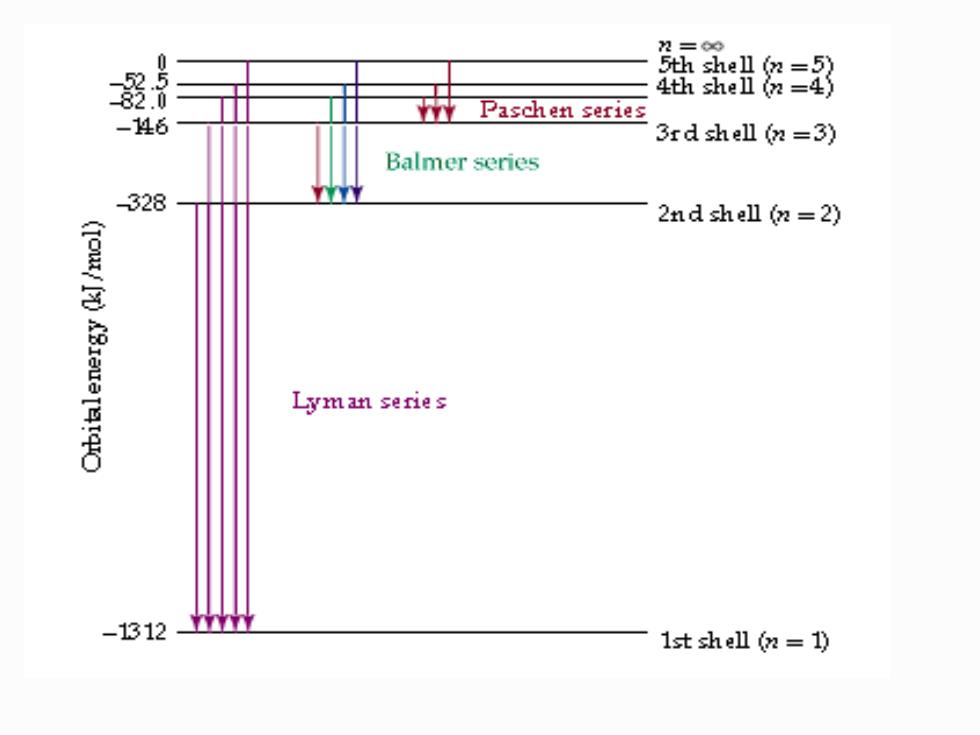
2=0 盘盆出符= -146 Paschen series 3rd shell (n=3) Balmer series 328 2nd shell (n=2) (IOW/M)ABauaIetqc Lyman series -1312 、 1st shell (n 1)

Balmer经验公式 o=1.09677×107(1/22-1/n2)m1 n=3,红(H) n=4,青(H) n=5,蓝(H) n=6,紫 (Hò) 其它线系: o=1/m=Rg×(1/12-1/n22)RH=1.09677×107m1 (1=1,2,3,.2=1+1,1+2.) n1=2可见光谱 n=1紫外光谱n1=3红外光谱
Balmer 经验公式 σ =1.09677107 (1 / 22 – 1/ n2 )m-1 n = 3, 红(Hα) n = 4, 青(Hβ) n = 5,蓝(Hγ) n = 6,紫(Hδ) 其它线系: σ = 1/ = RH (1/n1 2 – 1/n2 2 ) RH = 1.09677107 m-1 (n1 = 1,2,3,. n2 = n1 + 1 , n1 +2.) n1=2 可见光谱 n1=1紫外光谱 n1=3 红外光谱

o=1/八=RH×(1/m12-1/n22)RH=1.09677×107mr1 里德堡常数: R-1.09677×107ml 波数:k,o,v单位m, v=RH×(1/n12-1/m22)R=3.289×1015S-1 频率:V,单位Sl。 入=c/y=c/八o=1/八=coC=2.998×108mS-1 △E=RH×(1/m12-1/n22)RH=2.179×10-18J AE=hy=hco h=6.626X10-34J-S
σ = 1/ = RH (1/n1 2 – 1/n2 2 ) RH = 1.09677107 m-1 里德堡常数: RH=1.09677107 m-1 波数:k,σ,v 单位m-1; v = RH (1/n1 2 – 1/n2 2 ) RH=3.2891015 S -1 频率: ν,单位S -1 。 = c /ν ν= c / σ = 1/ ν= cσ C=2.998 108m·S -1 ΔE= RH (1/n1 2 – 1/n2 2 ) RH=2.17910-18 J ΔE = hν = hcσ h = 6.626×10-34J·S

5.1.3玻尔理论 1913年,丹麦物理学家N.Bohr根据: 1.Plank量子论(1900年) 微观领域能量不连续 2.Einstein光子论(1903年) E-hv E:光子的能量;v:光的频率; h:P1ank常数(6.626×10-34JS) 3.卢瑟福原子带核模型 建立了氢原子核外电子运动模 型。后人称为玻尔理论
5.1.3 玻尔理论 1913年,丹麦物理学家N.Bohr根据: 1.Plank量子论(1900年) 微观领域能量不连续 2.Einstein光子论(1903年) E=hν E:光子的能量;ν:光的频率; h:Plank常数(6.626×10-34J·S) 3.卢瑟福原子带核模型 建立了氢原子核外电子运动模 型。后人称为玻尔理论

玻尔理论的要点 1行星模型:氢原子核外电子是处在一定 的线性轨道上绕核运行的。这些轨道称为 稳定轨道,电子在稳定轨道上运动不释放 能量。 2.定态假设:建立了定态、基态、激发态 的概念
玻尔理论的要点 1.行星模型:氢原子核外电子是处在一定 的线性轨道上绕核运行的。这些轨道称为 稳定轨道,电子在稳定轨道上运动不释放 能量。 2.定态假设:建立了定态、基态、激发态 的概念