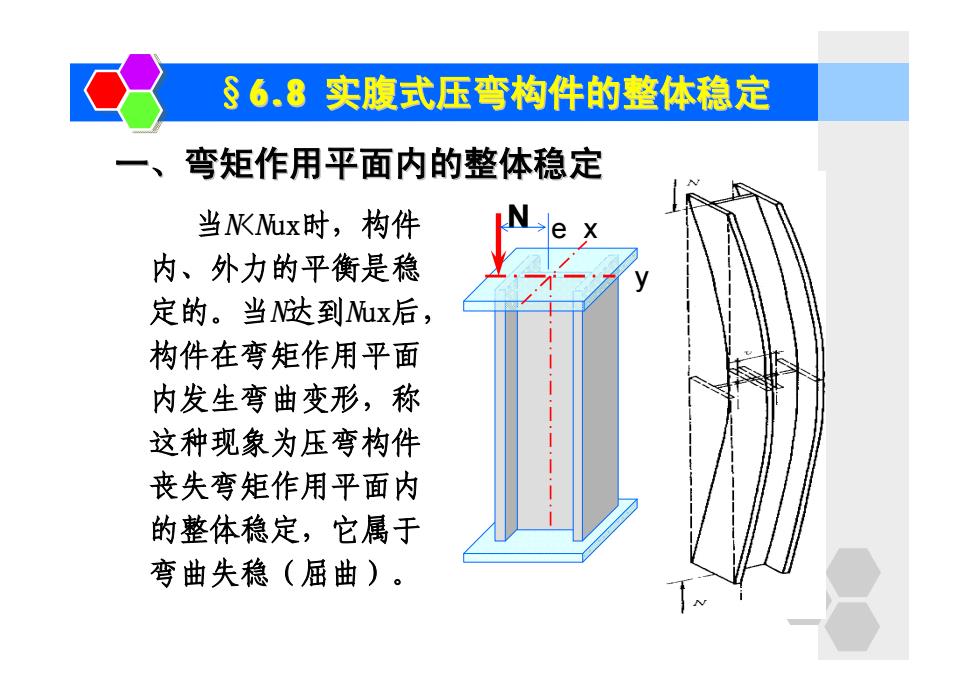
§6.8实腹式压弯构件的整体稳定 一、 弯矩作用平面内的整体稳定 当Kux时,构件 内、外力的平衡是稳 定的。当达到x后, 构件在弯矩作用平面 内发生弯曲变形,称 这种现象为压弯构件 丧失弯矩作用平面内 的整体稳定,它属于 弯曲失稳(屈曲)
§6.8 实腹式压弯构件的整体稳定 一、弯矩作用平面内的整体稳定 当N<Nux时,构件 内、外力的平衡是稳 定的。当N达到Nux后, 构件在弯矩作用平面 内发生弯曲变形,称 这种现象为压弯构件 丧失弯矩作用平面内 的整体稳定,它属于 弯曲失稳(屈曲)。 N e x y

§6.8实腹式压弯构件的整体稳定 弯矩作用平面内的整体稳定 N BnxM A YWx(1-0.81 N'gs NEx/1.1,NE =T2EA/ 0.8-修正系数; p.-弯矩作用平面内轴压构件的稳定系数; Wx-在弯矩作用平面内对较大受压纤维的 3 毛截面模量; Yx-塑性发展系数; Pm-等效弯矩系数
§6.8 实腹式压弯构件的整体稳定 一、弯矩作用平面内的整体稳定 f N N W M A N x x x £ ¢ - × + (1 0.8 ) E 1x mx x g b j 等效弯矩系数 塑性发展系数; 毛截面模量; 在弯矩作用平面内对较 大受压纤维的 弯矩作用平面内轴压构 件的稳定系数; 修正系数 , - - - - - ¢ = = mx x x x Ex Ex Ex x W N N N EA b g j p l 1 2 0.8 ; 1.1

§6.8实腹式压弯构件的整体稳定 弯矩作用平面内的整体稳定 mx·M ≤f Bn- 如何取值? A yW(1-0.8 -为何引入? Ex Bm=M<mx/aM称为等效弯矩系数。 利用B,就可以把各种荷载作用的弯矩 分布形式转化为均匀受弯者来看待
§6.8 实腹式压弯构件的整体稳定 f N N W M A N x x x £ ¢ - × + (1 0.8 ) E 1x mx x g b j 分布形式转化为均匀受 弯者来看待。 利用 就可以把各种荷载作用 的弯矩 称为等效弯矩系数。 mx mx M x M b b = max /a 为何引入? 如何取值? - b mx - 一、弯矩作用平面内的整体稳定

§68实腹式压弯构件的整体稳定 一、 弯矩作用平面内的整体稳定 对于单轴对称截面,当弯矩使较大翼缘受压时, 受拉区可能先受拉出现塑性,为此应满足: YW2x(1-1.25 式中: N Wx-对无翼缘端(受拉边缘)的毛截面模量; 其余符号同前
§6.8 实腹式压弯构件的整体稳定 对于单轴对称截面,当弯矩使较大翼缘受压时, 受拉区可能先受拉出现塑性,为此应满足: f N N W M A N £ ¢ (1 - 1.25 ) Ex x 2x mx x g b - 其余符号同前。 对无翼缘端(受拉边缘 )的毛截面模量; 式中: W2 x - 一、弯矩作用平面内的整体稳定
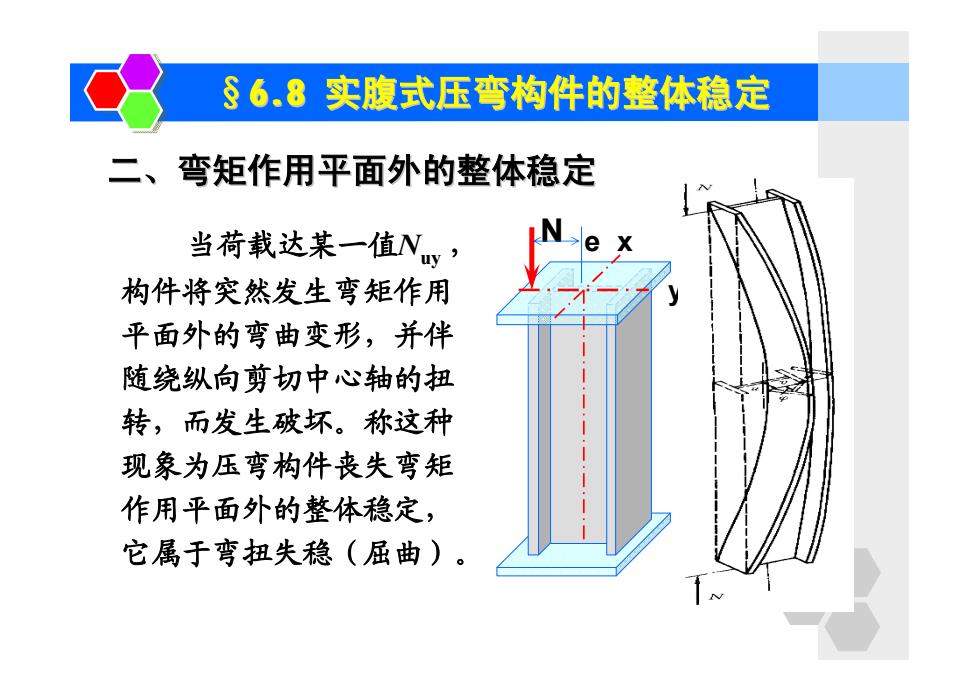
§6.8实腹式压弯构件的整体稳定 二、弯矩作用平面外的整体稳定 当荷载达某一值Ny, 构件将突然发生弯矩作用 平面外的弯曲变形,并伴 随绕纵向剪切中心轴的扭 转,而发生破坏。称这种 现象为压弯构件丧失弯矩 作用平面外的整体稳定, 它属于弯扭失稳(屈曲)
§6.8 实腹式压弯构件的整体稳定 二、弯矩作用平面外的整体稳定 当荷载达某一值Nuy , 构件将突然发生弯矩作用 平面外的弯曲变形,并伴 随绕纵向剪切中心轴的扭 转,而发生破坏。称这种 现象为压弯构件丧失弯矩 作用平面外的整体稳定, 它属于弯扭失稳(屈曲)。 N e x y