
最优解的特点 ,讨论3、一一单个不等式约束问题: ,理解: 。线性不等式将空间划分为两个区域,代价函数和不等式约束各自约 束一个空间,对任意△x都满足,说明在不等式约束的可行解集空 间和代价函数约束的空间的补空间交集为空集,即: 时(x内<0 不满足条件域 7c.(x的≥0
讨论3、——单个不等式约束问题: 理解: ◦ 线性不等式将空间划分为两个区域,代价函数和不等式约束各自约 束一个空间,对任意Δx都满足,说明在不等式约束的可行解集空 间和代价函数约束的空间的补空间交集为空集,即: 不满足条件域

最优解的特点 ,理解: {Ax|Vf(x*)Ax<O}∩{Ax|VCie(x*)Ax≥0}=φ 7c(x的≥0 交集为空集 Vf(x*)=27Cie(x*),元>0 f(x莉<0
理解: 交集为空集 f Cie ( *) ( *), x x 0 x x x x x x | ( *) 0 | ( *) 0 f Cie 1
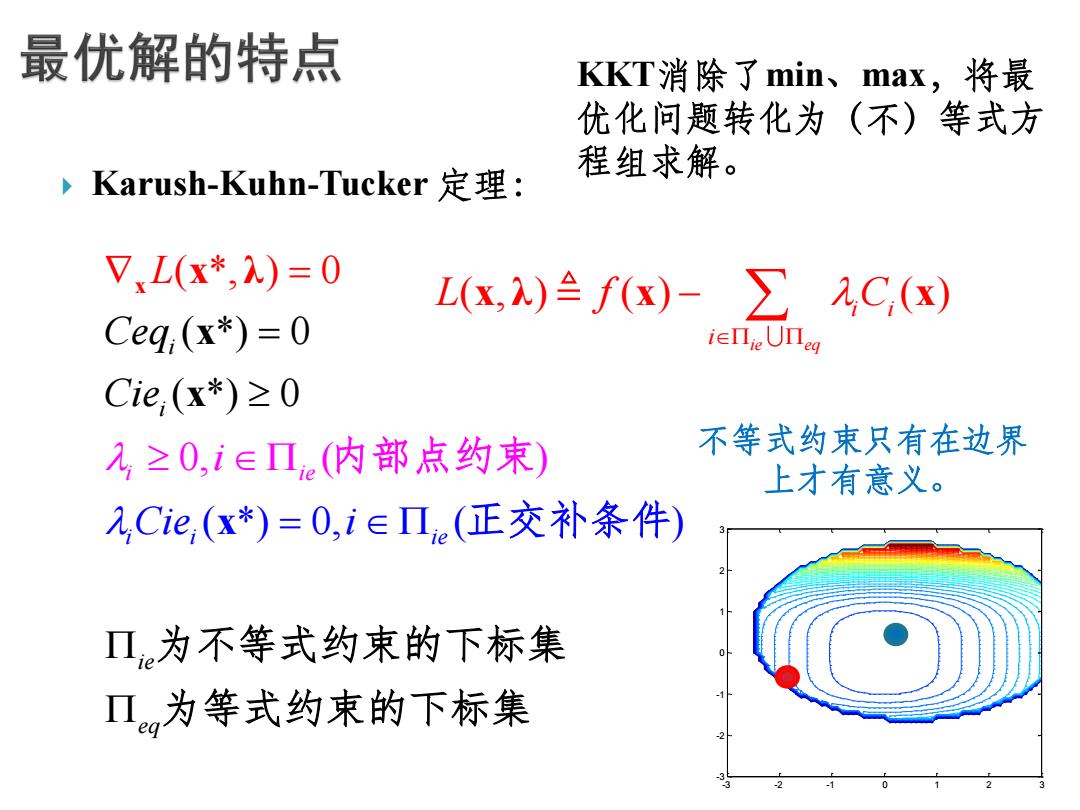
最优解的特点 KKT消除了min、max,将最 优化问题转化为(不)等式方 程组求解。 Karush-Kuhn-Tucker定理: V、L(x*,入)=0 L(x,)ef(x)-∑,C,(x) Ceq,(x*)=0 ieIlieUneg Cie,(x*)≥0 入≥0,i∈Π(内部点约束) 不等式约束只有在边界 上才有意义。 2,Cie,(x*)=0,ieΠe(正交补条件) Π为不等式约束的下标集 Ⅱ为等式约束的下标集
Karush-Kuhn-Tucker 定理: ( ( *) 0 ( ( * 0, *) 0, ( ) ) 0 ( ) , *) 0 i i i i i ie ie q ie e Cie i Ceq Cie i L x x λ x x x 正交补 为不等式约束的下标集 为等式 条 约 内部点约 件 束 束的下标集 KKT消除了min、max,将最 优化问题转化为(不)等式方 程组求解。 ( , ) ( ) ( ) ie eq i i i L f C x λ x x -3 -2 -1 0 1 2 3 -3 -2 -1 0 1 2 3 不等式约束只有在边界 上才有意义
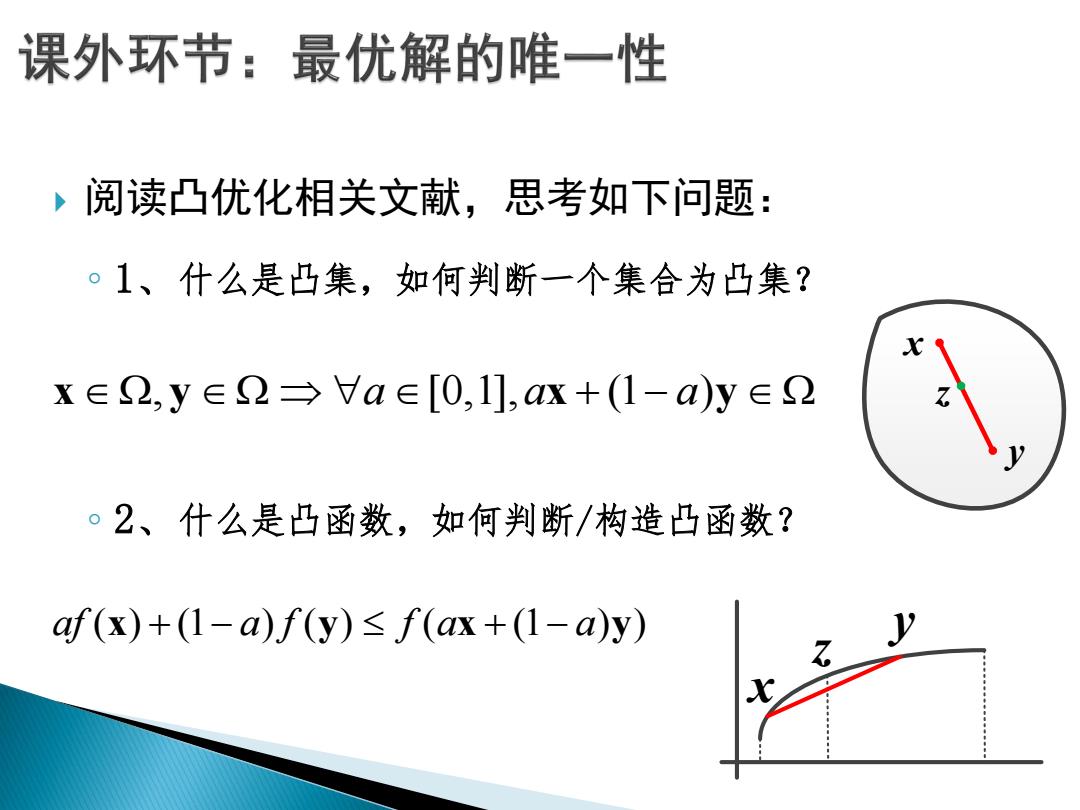
课外环节:最优解的唯一性 ,阅读凸优化相关文献,思考如下问题: 。1、什么是凸集,如何判断一个集合为凸集? x∈2,y∈2→Va∈[0,1],ax+(1-a)y∈2 。2、什么是凸函数,如何判断/构造凸函数? af(x)+(1-a)f(y)<f(ax+(1-a)y)
阅读凸优化相关文献,思考如下问题: ◦ 1、什么是凸集,如何判断一个集合为凸集? ◦ 2、什么是凸函数,如何判断/构造凸函数? x y x y , [0,1], (1 ) a a a x y z af a f f a a ( ) (1 ) ( ) ( (1 ) ) x y x y x y z
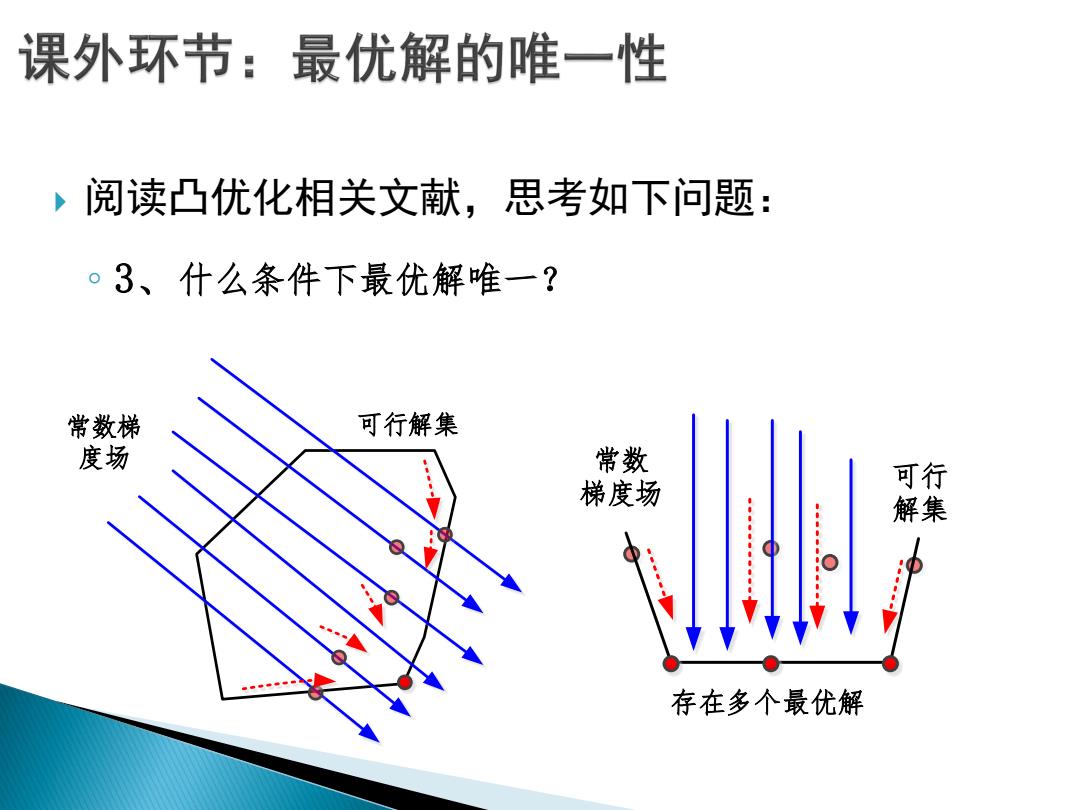
课外环节:最优解的唯一性 ,阅读凸优化相关文献,思考如下问题: 。3、什么条件下最优解唯一? 常数梯 可行解集 度场 常数 梯度场 可行 解集 存在多个最优解
阅读凸优化相关文献,思考如下问题: ◦ 3、什么条件下最优解唯一? 可行 解集 常数 梯度场 存在多个最优解 常数梯 可行解集 度场