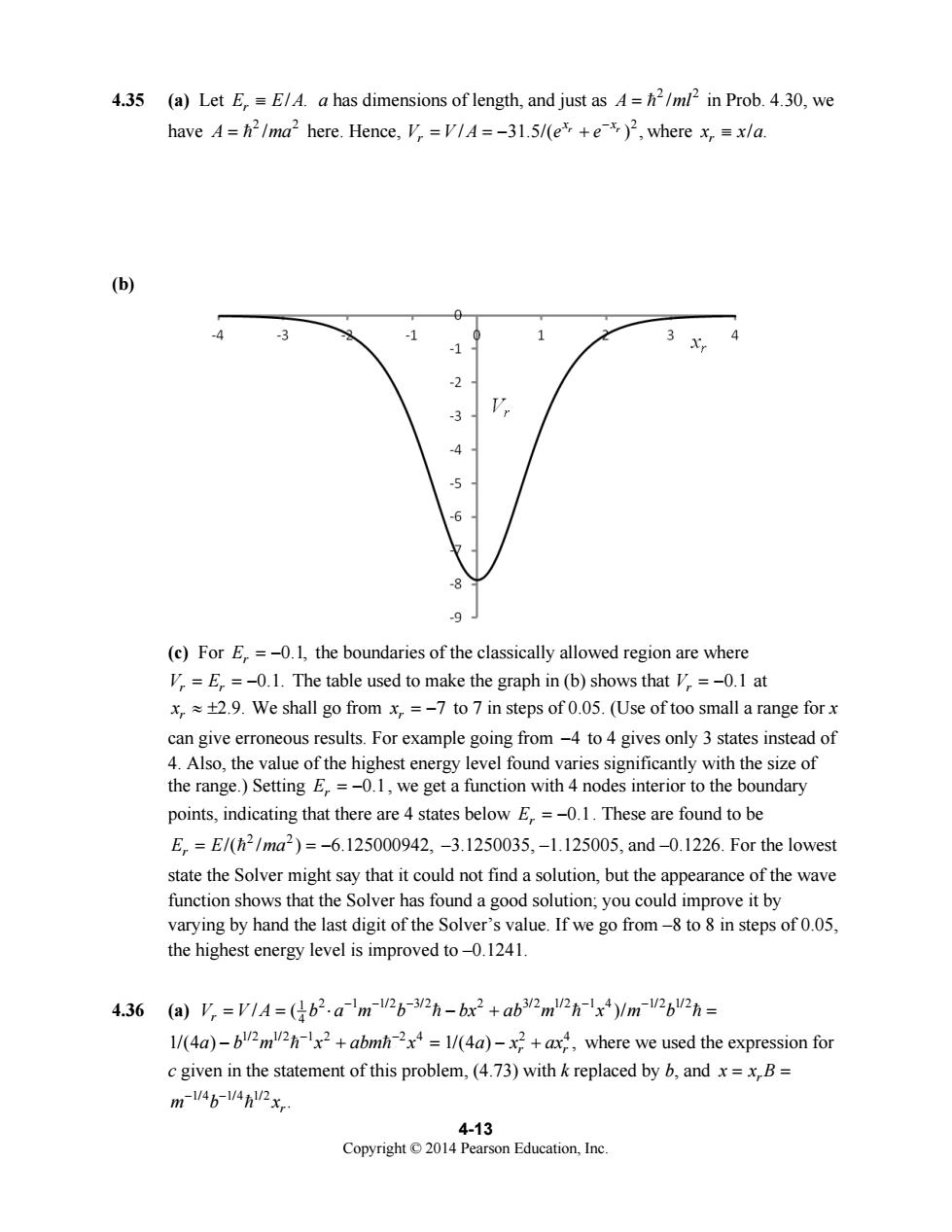
4.35 (a)Let E,=E/A.a has dimensions of length,and just as =h2/ml2 in Prob.4.30,we have A=h2/ma2 here.Hence,V =V/A=-31.5/(e +e)2,where x =x/a. (b) A -3 -1 1 3X4 3 9 (c)For E=-0.1,the boundaries of the classically allowed region are where I=E =-0.1.The table used to make the graph in (b)shows that I=-0.1 at x2.9.We shall go from x=-7 to 7 in steps of 0.05.(Use of too small a range for can give erroneous results.For example going from-4 to4 gives only 3 states instead of 4.Also,the value of the highest energy level found varies significantly with the size of the range.)Setting E=-0.1,we get a function with 4 nodes interior to the boundary points,indicating that there are 4 states below E=-0.1.These are found to be E,=E/(h2/ma2)=-6.125000942,-3.1250035,-1.125005,and-0.1226.For the lowest state the Solver might say that it could not find a solution,but the appearance of the wave function shows that the Solver has found a good solution;you could improve it by varying by hand the last digit of the Solver's value.If we go from-8 to 8 in steps of .05, the highest energy level is improved to-0.1241. 4.36 (a)V=VIA=(162.am2b-h-bx2+ab2m2hx)/m-2bn= 1/(4a)-b2m2x+abmh=1/(4a)-+ax,where we used the expression fo c given in the statement of this problem,(4.73)with k replaced by b,andx=xB= m14b-14n2x, 4-13 Education.Inc
4-13 Copyright © 2014 Pearson Education, Inc. 4.35 (a) Let / . E EA r ≡ a has dimensions of length, and just as 2 2 A ml = = / in Prob. 4.30, we have 2 2 A = = /ma here. Hence, 2 / 31.5/( ) , r r x x V VA e e r − = =− + where / . r x ≡ x a (b) (c) For 0.1, Er = − the boundaries of the classically allowed region are where 0.1. V E r r = =− The table used to make the graph in (b) shows that 0.1 Vr = − at 2.9. r x ≈ ± We shall go from 7 r x = − to 7 in steps of 0.05. (Use of too small a range for x can give erroneous results. For example going from 4− to 4 gives only 3 states instead of 4. Also, the value of the highest energy level found varies significantly with the size of the range.) Setting 0.1 Er = − , we get a function with 4 nodes interior to the boundary points, indicating that there are 4 states below 0.1 Er = − . These are found to be 2 2 /( / ) 6.125000942, E E ma r = =− = –3.1250035, –1.125005, and –0.1226. For the lowest state the Solver might say that it could not find a solution, but the appearance of the wave function shows that the Solver has found a good solution; you could improve it by varying by hand the last digit of the Solver’s value. If we go from –8 to 8 in steps of 0.05, the highest energy level is improved to –0.1241. 4.36 (a) 1 2 1 1/2 3/2 2 3/2 1/2 1 4 1/2 1/2 4 / ( )/ V V A b a m b bx ab m x m b r −− − − − = = ⋅ −+ = = == 1/2 1/2 1 2 2 4 1/(4 ) a b m x abm x − − − += = = 2 4 1/(4 ) , r r a x ax − + where we used the expression for c given in the statement of this problem, (4.73) with k replaced by b, and r x = = x B 1/4 1/4 1/2 . mb xr − − =
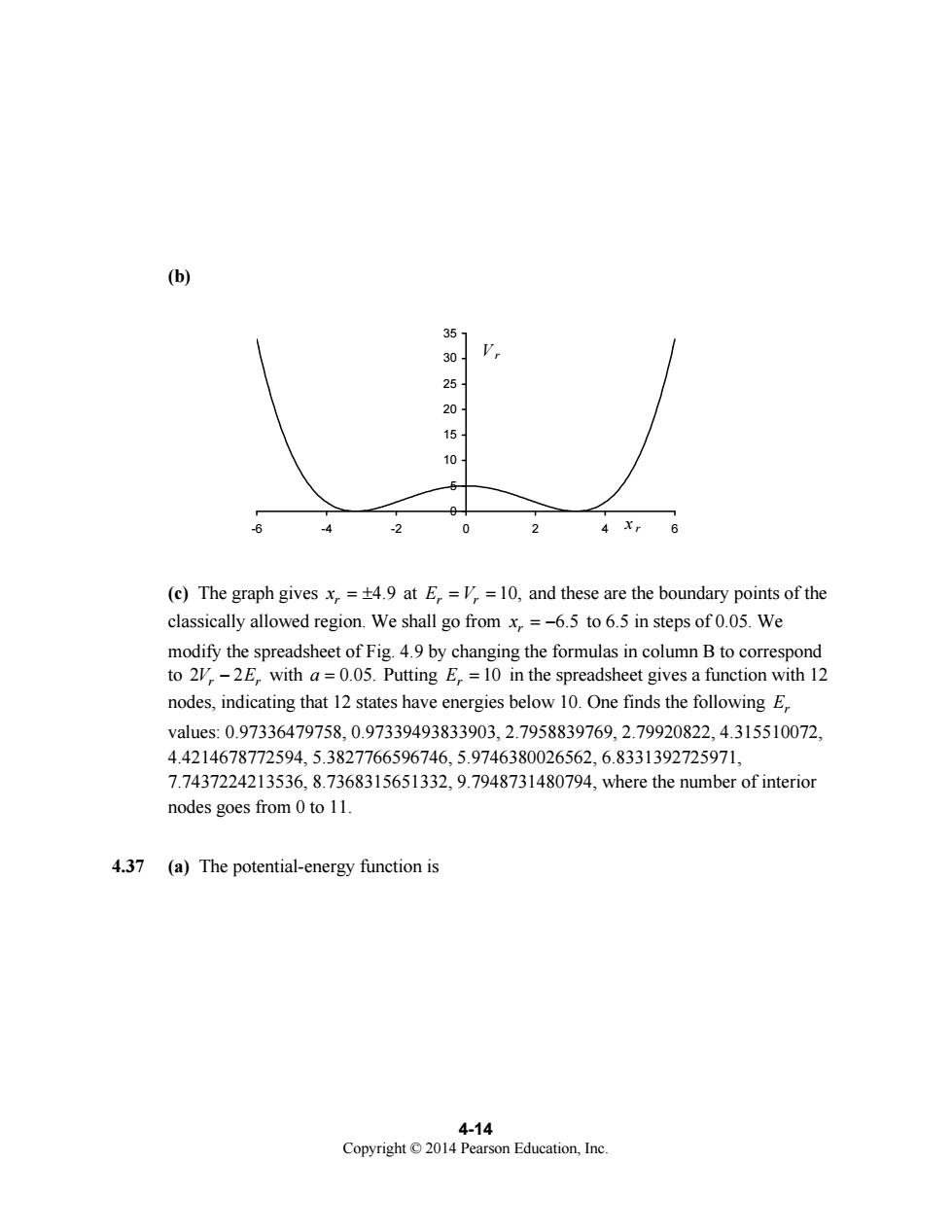
(b) 20 15 10 2 0 2 (c)The graph gives x=4.9 at E=V=10.and these are the boundary points of the classically allowed region.We shall go from x,=-6.5 to 6.5 in steps of 0.05.We nd to 2,-2E,with a=0.05.Putting E=10 in the spreadsheet gives a function with 12 nodes,indicating that 12 states have energies below 10.One finds the following E values:0.97336479758,0.97339493833903.2.7958839769,2.79920822,4.315510072, 4.4214678772594,5.3827766596746,5.9746380026562,6.8331392725971, 7.7437224213536,8.7368315651332,9.7948731480794,where the number of interior nodes goes from 0 to 11. 4.37 (a)The potential-energy function is 4-14 Copyright2014 Pearson Education.Inc
4-14 Copyright © 2014 Pearson Education, Inc. (b) 0 5 10 15 20 25 30 35 -6 -4 -2 0 2 4 6 V r x r (c) The graph gives 4.9 r x = ± at 10, E V r r = = and these are the boundary points of the classically allowed region. We shall go from 6.5 r x = − to 6.5 in steps of 0.05. We modify the spreadsheet of Fig. 4.9 by changing the formulas in column B to correspond to 2 2 V E r r − with a = 0.05. Putting 10 Er = in the spreadsheet gives a function with 12 nodes, indicating that 12 states have energies below 10. One finds the following Er values: 0.97336479758, 0.97339493833903, 2.7958839769, 2.79920822, 4.315510072, 4.4214678772594, 5.3827766596746, 5.9746380026562, 6.8331392725971, 7.7437224213536, 8.7368315651332, 9.7948731480794, where the number of interior nodes goes from 0 to 11. 4.37 (a) The potential-energy function is

-1-1 As in the particle in a box (Prob.4.30)E=E/(h2 /m2),=x/I.x,goes from-0.5 to 0.5.We shall take s =0.01.A cell is designated to contain the value of Vo.The column B cells contain the formula for 2V-2E,where V is 0 for-0.5sx s-0.25 and for 0.25sx s0.5;and is Vo,for -0.25<x <0.25.One finds E =E/(h2/ml2)= 5.7400863,20.216046,44.798915,79.459117.The wave functions closely resemble those of a particle in a box(pib).This is because the bound-state energies are all substantially greater than so o is only a small perturbation on the pib potential energy (b)With Vor changed to 100.one finds E=E/(h2/m)=44.4763188,44.7856494. 113.73536239.142.13947708. (c)With%=1000,we get E,=63.869414269,63.869414294,254.025267141, 254.025267989.The first two states have wave functions that look like particle-in-box n0 functions in the left and right quarters of the well with being small in the central regon,and the next two wave functions in these two quarters The energies of these states are well below o.In the limit oo,we would have two boxes with infinitely high walls 4.38(a0.4999996,1.4999973,2.4999903,3.4999765,4.4999621,5.5000081,11.7121.The range-5 to5 was chosen as appropriate for reduced energies less than 5.For E=11.5. the classically allowed region is found from 0.5x2=11.5 and x=4.8.At x=5,we are not far enough into the classically forbidden region to approximate as zero.If we redo things with the range taken from65 we (b)0.499747,1.498209,2.493505,3.483327,4.465124,5.436066.The larger s,value reduces the accuracy. (c)0.500391,1.506079,2.541116,3.664184,4.954083. 4-15 Copyright2014 Pearson Education.Inc
4-15 Copyright © 2014 Pearson Education, Inc. As in the particle in a box (Prob. 4.30) 2 2 /( / ), / . E E ml x x l r r = = = r x goes from −0.5 to 0.5. We shall take 0.01. rs = A cell is designated to contain the value of V0,r . The column B cells contain the formula for 2 2 , V E r r − where Vr is 0 for 0.5 0.25 r − ≤ ≤− x and for 0.25 0.5; r ≤ ≤ x and is V0,r for 0.25 0.25. r − < < x One finds 2 2 /( / ) E E ml r = = = 5.7400863, 20.216046, 44.798915, 79.459117. The wave functions closely resemble those of a particle in a box (pib). This is because the bound-state energies are all substantially greater than V0 , so V0 is only a small perturbation on the pib potential energy. (b) With V0,r changed to 100, one finds 2 2 /( / ) E E ml r = = = 44.4763188, 44.7856494, 113.73536239, 142.13947708. (c) With 0, 1000 V r = , we get Er = 63.869414269, 63.869414294, 254.025267141, 254.025267989. The first two states have wave functions that look like particle-in-box n = 0 functions in the left and right quarters of the well with ψ being small in the central region, and the next two wave functions resemble n = 1 functions in these two quarters. The energies of these states are well below V0 . In the limit V0 → ∞ , we would have two boxes with infinitely high walls. 4.38 (a) 0.4999996, 1.4999973, 2.4999903, 3.4999765, 4.4999621, 5.5000081; 11.7121. The range –5 to 5 was chosen as appropriate for reduced energies less than 5. For 11.5, Er = the classically allowed region is found from 2 0.5 11.5 r x = and 4.8. r x = ± At 5 r x = ± , we are not far enough into the classically forbidden region to approximate ψ as zero. If we redo things with the range taken from –6.5 to 6.5 with 0.1, rs = we get 11.49921. (b) 0.499747, 1.498209, 2.493505, 3.483327, 4.465124, 5.436066. The larger rs value reduces the accuracy. (c) 0.500391, 1.506079, 2.541116, 3.664184, 4.954083. ∞ ∞ V0 1 2 − l 1 4 − l 1 2 l 1 4 l V x

4.39 (a)The usual mathematical convention is that-x2+x2=0.Hence one would expect 0 as the result. (b)Excel gives 50.Certain other spreadsheets give 0. 4.40 (b)x2 can be misinterpreted as a cell reference,so x2 is not allowed as the name of a parameter. 4.41 Put n=1 in(4.67).Since o=0,(4.67)shows that wz is proportional to w.With n=2. (4.67)shows that wa contains only terms linear in v and y,and since v is proportional to is proportional to v.With n=2.(4.67)shows that w contains only terms linear in and and since both of these are proportional tois proportional to w.And so on. 4.42 For the v=0 state with E =0.5,the boundaries of the classically allowed region are found from 0.5=0.5x2 and thus arex=1.The probability of being in the classically forbidden region is 2.We square the normalized column E values to get values in column F.We approximate this probability by 2(0.1),where the sum uses the column F values from-5 to-1.Since the value at-1 is at the boundary of the allowed and forbidden regions,we shall include one-half thevalue at-1 in the sum.We get 0.16 as the probability of being in the classically forbidden region.For the E =1.5 state,the boundaries of the classically allowed region satisfy 1.5=0.5x2 and x=+1.73.Taking twice the sum from-5 to-1.7 for this state,we get 0.12 as the probability of being in the classically forbidden region.This is smaller than 0.16.in accord with the correspondence principle. 4.43 (a)With this notation,(4.85)becomes fn+)=f,)+fx,5+f"x,52+f(x3+六fx)+高f6x,s3+. (b)Replacement ofs by-s gives fxn-s)=fxn)-f"(xn)s+支f"(xn)s2-f(xn)s3+太f(xn)s-f(xn)s3+. Addition of these two equations and neglect ofsand higher powers gives f(xn+s)+f(xn-s)=2f(x)+f"(x)s2+f(x)s4 Use of the notation of (4.65)with wreplaced by f followed by the replacement off by gives 4-16 Copyright2014 Pearson Education.Inc
4-16 Copyright © 2014 Pearson Education, Inc. 4.39 (a) The usual mathematical convention is that 2 2 −x x + = 0. Hence one would expect 0 as the result. (b) Excel gives 50. Certain other spreadsheets give 0. 4.40 (b) x2 can be misinterpreted as a cell reference, so x2 is not allowed as the name of a parameter. 4.41 Put n = 1 in (4.67). Since 0 ψ = 0, (4.67) shows that ψ 2 is proportional to ψ1. With n = 2, (4.67) shows that ψ 3 contains only terms linear in ψ 2 and ψ1, and since ψ 2 is proportional to ψ1, ψ 3 is proportional to ψ1. With n = 2, (4.67) shows that ψ 4 contains only terms linear in ψ 3 and ψ 2 and since both of these are proportional to ψ1, ψ 4 is proportional to ψ1. And so on. 4.42 For the v = 0 state with 0.5, Er = the boundaries of the classically allowed region are found from 2 0.5 0.5 r = x and thus are 1 r x = ± . The probability of being in the classically forbidden region is 1 2 5 2|| r r ψ dx − −∫ . We square the normalized ψ r column E values to get 2 | | ψ r values in column F. We approximate this probability by 2 2 | | (0.1), ∑ ψ r where the sum uses the column F values from –5 to –1. Since the value at –1 is at the boundary of the allowed and forbidden regions, we shall include one-half the 2 | | ψ r value at –1 in the sum. We get 0.16 as the probability of being in the classically forbidden region. For the 1.5 Er = state, the boundaries of the classically allowed region satisfy 2 1.5 0.5 r = x and 1.73. r x = ± Taking twice the sum from –5 to –1.7 for this state, we get 0.12 as the probability of being in the classically forbidden region. This is smaller than 0.16, in accord with the correspondence principle. 4.43 (a) With this notation, (4.85) becomes 11 1 1 2 3 (iv) 4 (v) 5 2 6 24 120 ( ) () () () () () () n nn n n n n fx s fx f x s f x s f x s f x s f x s += + + + + + + ′ ′′ ′′′ " (b) Replacement of s by –s gives 11 1 1 2 3 (iv) 4 (v) 5 2 6 24 120 ( ) () () () () () () n nn n n n n fx s fx f x s f x s f x s f x s f x s −= − + − + − + ′ ′′ ′′′ " Addition of these two equations and neglect of s 6 and higher powers gives 2 (iv) 4 1 12 ( ) ( ) 2( ) ( ) ( ) n n nn n f x s fx s fx f x s f x s ++ −≈ + + ′′ Use of the notation of (4.65) with ψ replaced by f followed by the replacement of f by ψ gives

1*-1+2n+2+立g (4.87) "a-Ψm-1+2yn+yn2+立wmg (4.88) (c)Replacement off in(4.87)withand multiplication by sgives 1-yw2+2y2+wmg4+tmg6 Neglecting the s term,we get ws4≈w+1s2+i-1s2-20s2 Use of=G in this last equation gives Ws GWms2+Gn-W-2-2GWns2 (4.89) Substitution of (4.89)and y"=Gy into (4.88)gives Vm =V1+2+GGm+G-W-2G Solving this last equation for we get Eq.(4.67). 4.44 Let B=mkh Then(4.70)and (4.71)give [B]=[mKW]=M (MT-2)(MLT-Y=M/L2/T2-L d+e+f=0,2f=l,-2e-f=0 f=,e=-4,d=- B=m4k-/4h/2 4.45 (a)From-(h2/2m)y"+V(x)y Ev,we get w"(a)=0 if w(a)=0 and V(a)is finite (b)Differentiation of the Schrodinger equation gives(/2m+V=Ev' Then if both and are zero at a and 'is finite at a.we get(a)=0.Further differentiation of the Schrodinger equation then shows all higher derivatives are zero ata 4.46 (a)Vis the same as in Prob.4.33,except that c replaces a.From the Prob.4.33 solution, =xlm non5c-no.E,-EIA=EIm 45n5cls and V,=VIA=VIm 455cs cx Im 45h5cus =cx(m-onsc-no)/m 4/5h5cs=x.The classically allowed region has Ethat is,0 which gives=1.33 and -1.33≤x≤133. 4-17 Copyright2014 Pearson Education.Inc
4-17 Copyright © 2014 Pearson Education, Inc. 2 4 1 ( ) iv 1 1 12 2 n n nn n f f f fs f s + − ≈− + + + ′′ (4.87) 2 4 1 ( ) iv 1 1 12 2 n n nn n ψ ψ ψψ ψ s s + − ≈− + + + ′′ (4.88) (c) Replacement of f in (4.87) with ψ′′ and multiplication by s 2 gives 2 2 2 (iv) 4 (vi) 6 1 1 1 12 2 n n nn n ψ′′ ′′ ′′ + − s ss s s ≈− + + + ψ ψψ ψ Neglecting the s 6 term, we get (iv) 4 2 2 2 1 1 2 n nn n ψ ψψ ψ s s ss + − ≈+− ′′ ′′ ′′ Use of ψ′′ = Gψ in this last equation gives (iv) 4 2 2 2 11 11 2 n n n n n nn ψ ψ ψψ sG sG s Gs ≈+− ++ −− (4.89) Substitution of (4.89) and ψ′′ = Gψ into (4.88) gives 2 2 22 1 1 1 11 11 12 2 2 ψ n n n nn n n n n nn ψψψ ψ ψ ψ Gs G sG s Gs + − ++ −− ≈− + + + + − ⎡ ⎤ ⎣ ⎦ Solving this last equation for ψ n+1 , we get Eq. (4.67). 4.44 Let = . def B mk = Then (4.70) and (4.71) give [ ] ( ) ( ) 2 21 2 2 M MT ML T M L T L e f d e f d def f ef B mk − − ++ − − == = = ⎡ ⎤ ⎣ ⎦ = def f ef ++ = = − − = 0, 2 1, 2 0 11 1 24 4 fe d = , , =− =− 1/4 1/4 1/2 Bm k − − = = 4.45 (a) From 2 − += ( /2 ) ( ) = m Vx E ψ′′ ψ ψ , we get ( ) 0 ψ′′ a = if ( ) 0 ψ a = and ( ) V a is finite. (b) Differentiation of the Schrödinger equation gives 2 − ++= ( /2 ) = m VV E ψ′′′ ′ ′ ′ ψ ψψ . Then if both ψ and ψ′ are zero at a and V′ is finite at a, we get ψ′′′() 0 a = . Further differentiation of the Schrödinger equation then shows all higher derivatives are zero at a. 4.46 (a) V is the same as in Prob. 4.33, except that c replaces a. From the Prob. 4.33 solution, 1/10 1/5 1/10 / r x xm c − − = = , 4/5 8/5 1/5 / / Er EA Em c − = = = and 4/5 8/5 1/5 / / V VA Vm c r − = = = = 8 4/5 8/5 1/5 8 1/10 1/5 1/10 8 4/5 8/5 1/5 8 / ( )/ . r r cx m c cx m c m c x − −−− = == = = The classically allowed region has , E V r r ≥ that is, 8 10 r ≥ x , which gives 1/8 10 1.33 r x ≤ = and 1.33 1.33. r − ≤≤ x