
1=IcoP (1-4ax2+4a2x')e-ax dx =21 coP(1-4ax2+4a2x')e-ax dx =21c2[2l(z1a)2-4a/4)x21a32+4a2(3/8)x21a521=21c,P(x1a)2 where (A.9)and(A.10)were used.Hence co=2-2(/)4 41 1 From(447,43=(Gx+ex2emp.from(4.46.9=2al-3/6%=-2ac3.S0 W3=glx-(2/3)ax'len.We have 1=|926[x2-(4/3)ax+(4/9)a2x1 e-axdx= 216P[/22)x21a32-(4/3a3/23)x21a5n+(4/9a205/2*x21an]= IcPa 13 and I4.Then V3=3a[x-(213)ax'le-aR. 4.12 From(4.47),Wa e-ax'(co+c2x2+cx).From(4.46)with v=4 c2=2a(-4)c/2=-4 aco and c4=2a(2-4)e213.4)=-ac2/3=-a(-4ac)/3=4a2c13.Then Ws=coe-a(1-4ax+4ax3). 4.13 At the maxima in the probability density,we have/x=0.From(4.54), 0=c(0/0x)(x2e-ax)=c2(2x-2ax')e-ax,so 0=x-ax=x(1-ax2).The solutions are0andFrom Fig.isa minimum in probability density,so the maxima are at x=ta-2. 4.14 The wave function is an odd function with five nodes,one of which is at the origin. UV* Alternatively.one could take-1 times the w function graphed above. 4-3 Education.Inc
4-3 Copyright © 2014 Pearson Education, Inc. 2 2 2 2 24 2 2 24 0 00 1 | | (1 4 4 ) 2| | (1 4 4 ) x x c x x e dx c x x e dx α α αα αα ∞ ∞ − − = −+ = −+ ∫ ∫ −∞ 2 1 1/2 1/2 3/2 2 1/2 5/2 0 2 | | [2 ( / ) 4 (1/4) / 4 (3 / 8) / ] c πα α π α α π α − = −+ = 2 1/2 0 2| | ( / ) c π α where (A.9) and (A.10) were used. Hence 1/2 1/4 0 | | 2 (/) . c α π − = 4.11 From (4.47), 2 3 /2 313 ( ). ax ψ cx cx e− = + From (4.46), 3 11 c cc = [2 (1 3)/6] 2 /3. α − =− α So 2 3 /2 3 1[ (2/3) ] x cx xe α ψ α − = − . We have 2 2 2 4 26 1 0 1 | | 2 [ (4/3) (4/9) ] x c x x x e dx α α α ∞ − = −+ = ∫ 2 2 1/2 3/2 3 1/2 5/2 2 4 1/2 7/2 1 2 | | [(1/2 ) / (4/3) (3/2 ) / (4/9) (15/2 ) / ] c πα α πα α πα −+ = 2 1/2 3/2 1 | | /3 c π α− and 1/2 3/4 1/4 1 | |3 . c α π− = Then 2 1/2 3/4 1/4 3 /2 3 3 [ (2/3) ] . x x xe α ψ απ α − − = − 4.12 From (4.47), 2 2 4 4 02 4 ( ). x e c cx cx α ψ − = ++ From (4.46) with v = 4, 2 00 c cc = − =− 2 ( 4) /2 4 α α and 422 ccc = − ⋅ =− 2 (2 4) /(3 4) /3 α α 0 = − − α( 4 )/3 αc 2 0 = 4 /3. α c Then 2 2 24 4 0 (1 4 4 /3). x ce x x α ψ α α − = −+ 4.13 At the maxima in the probability density 2 | | ψ , we have 2 ∂ | | / 0. ψ ∂ = x From (4.54), 2 2 22 2 3 1 1 0 ( / )( ) (2 2 ) , x x c x xe c x x e α α α − − = ∂∂ = − so 3 2 0 (1 ). =− = − x α α xx x The solutions are x = 0 and 1/2 x α . − = ± From Fig. 4.4b, x = 0 is a minimum in probability density, so the maxima are at 1/2 x α . − = ± 4.14 The wave function is an odd function with five nodes, one of which is at the origin. Alternatively, one could take 1− times the ψ function graphed above
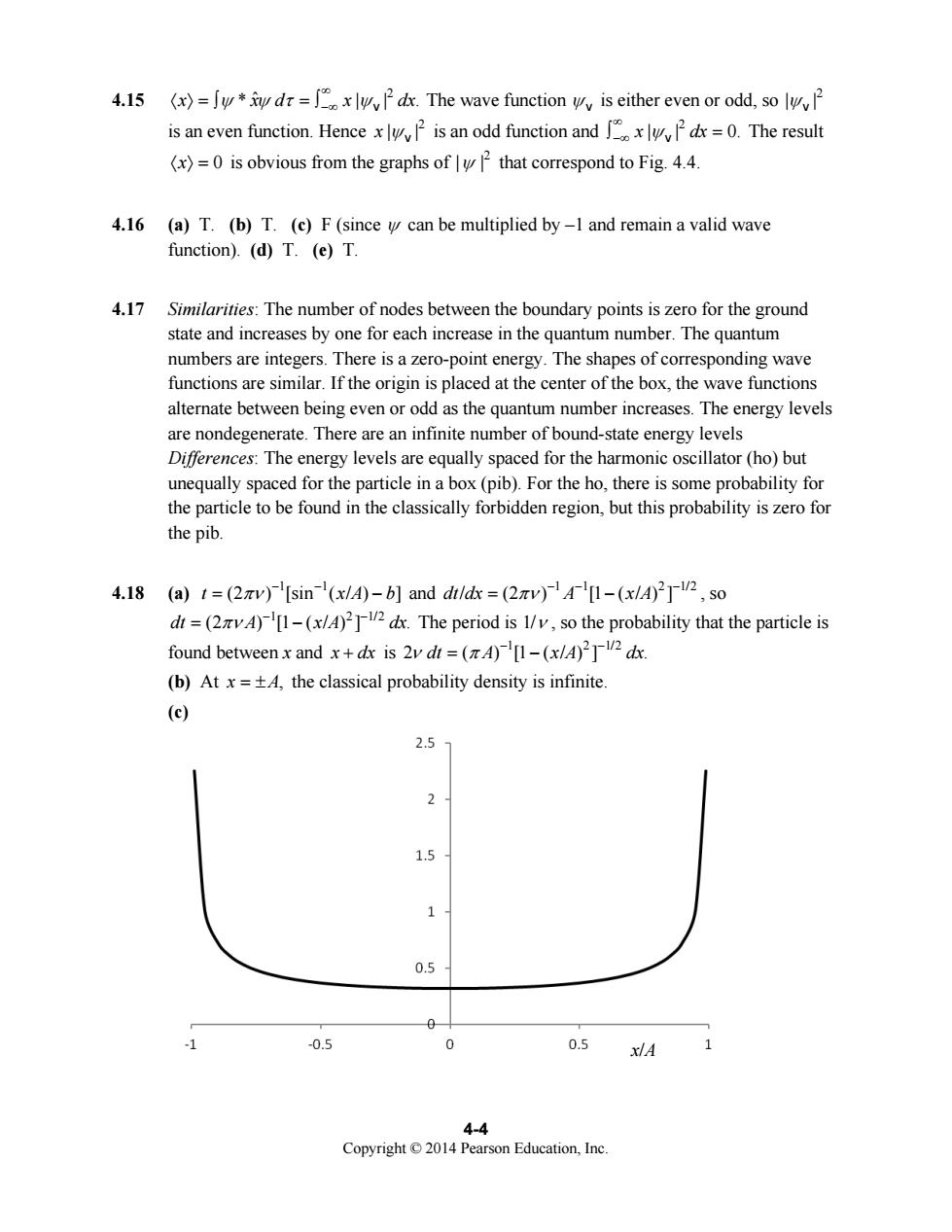
4.15 (x)=fy*d=Pdx.The wave function wy is either even or odd,so is an even function.Hencex is an odd function andx=0.The result (x)=0 is obvious from the graphs of that correspond to Fig.4.4. 4.16 (a)T.(b)T.(c)F(since can be multiplied by-1 and remain a valid wave function).(d)T.(e)T. 4.17 Similarities:The number of nodes between the boundary points is zero for the ground state and increases by one for each increase in the quantum number.The quantum numbers are integers.There is a zero-point energy.The shapes of corresponding wave functions are similar.If the origin is placed at the center of the box,the wave functions alternate between being even or odd as the quantum number increases.The energy levels are nondegenerate.There are an infinite number of bound-state energy levels Differences:The energy levels are equally spaced for the harmonic oscillator (ho)but unequally spaced for the particle in a box(pib).For the ho,there is some probability for the particle to be found in the classically forbidden region,but this probability is zero for the pib. 4.18 (a)t=(2v)[sin-(x/A)-b]and dildx =(2v)A1-(xlA)22,so di=(1-(x/)x.The period is /v,so the probability that the particle is found betweenx and x+dx is 2vdt=()[1-(x/A)22dx. (b)Atx=+A,the classical probability density is infinite. (c) 2.5 1.5 1 0.5 -0.5 0 0.5xA1 4-4 Copyright2014 Pearson Education.Inc
4-4 Copyright © 2014 Pearson Education, Inc. 4.15 2 x ψ ψτ ψ * || . x d x dx ˆ ∞ −∞ 〈 〉= =∫ ∫ v The wave function ψ v is either even or odd, so 2 | | ψ v is an even function. Hence 2 x | | ψ v is an odd function and 2 x dx | | 0. ψ ∞ −∞ ∫ v = The result 〈 〉= x 0 is obvious from the graphs of 2 | | ψ that correspond to Fig. 4.4. 4.16 (a) T. (b) T. (c) F (since ψ can be multiplied by –1 and remain a valid wave function). (d) T. (e) T. 4.17 Similarities: The number of nodes between the boundary points is zero for the ground state and increases by one for each increase in the quantum number. The quantum numbers are integers. There is a zero-point energy. The shapes of corresponding wave functions are similar. If the origin is placed at the center of the box, the wave functions alternate between being even or odd as the quantum number increases. The energy levels are nondegenerate. There are an infinite number of bound-state energy levels Differences: The energy levels are equally spaced for the harmonic oscillator (ho) but unequally spaced for the particle in a box (pib). For the ho, there is some probability for the particle to be found in the classically forbidden region, but this probability is zero for the pib. 4.18 (a) 1 1 t xA b (2 ) [sin ( / ) ] πν − − = − and 1 1 2 1/2 dt dx A x A / (2 ) [1 ( / ) ] πν −− − = − , so 1 2 1/2 dt A x A dx (2 ) [1 ( / ) ] . πν − − = − The period is 1/ν , so the probability that the particle is found between x and x + dx is 1 2 1/2 2 ( ) [1 ( / ) ] . ν π dt A x A dx − − = − (b) At x = ±A, the classical probability density is infinite. (c) x/A

For high values of the quantum number v,the outer peaks inare much higher than emotion,as for the c with the correspondence principle 4.19 Forx20,the Hamiltonian operator is the same as that of the harmonic oscillator.Hence the solutions of the Schrodinger equation forx20 are the functions(4.42),where the coefficients obey the recursion relation (4.39).To make wquadratically integrable.w gotoeThi ouday cditionthn stricts the soluions to the -oscillator functions(4.47).Since V is infinite be zero for x<0 (as for the particle in a box).The condition that u be continuous then requires that =0 at x=0.The even harmonic-oscillator functions in(4.47)are not zero at the origin,so these are eliminated.Hence the well-behaved solutions are the harmonic oscillator wave functions with v=1,3,5,.,and E=(v+)hv with v=1,3,5,.If we define n=(v-1)/2,then E=(2n+)h,with n=0,1,2,. 4.20 (a)The time-independent Schrodinger equation(3.47)is -(h212m)(8wlax2+8wlay2+8wlo2)+(kx2+ky+k.2=EV. The Hamio operator is the sum of terms that each involve only one coordinate.so we tryaseparation of variables,taking(()Substitution Schrodinger equation followed by division by fgh gives 是+h是+虑的g52+长产+达做-动 d 21d2 a+1d-g++kx2+iky2+ik.==E (Eq.1) 2(1dg+1d2h E1+k2=Et2mgh心2厂少-k之(Eq2) Since fis a function ofx only,the defined quantity E is independent ofy and=.Since E equals the right side of the last equation andx does not appear on this side,E is independent ofx.Therefore E is a constant.Multiplication of the E definition byf gives-(2/2m)(d2f/dx2)+=Ef,which is the same as the one-dimensional harmonic-oscillator (ho)Schrodinger equation(4.32)[see also(4.26)]with y replaced byf,k replaced byk,and E replaced by E.Hence f(x)is the one-dimensional ho wave function(4.47)with v replaced by v,and E is given by (4.45)and (4.23)as E=(v+v=(1/2)(k/m)2.Since x.y,and occur symmetrically,g(y)and h()are ho functions withy and=as the variable.Equations I and 2 give 45 Education.Inc
4-5 Copyright © 2014 Pearson Education, Inc. For high values of the quantum number v , the outer peaks in 2 ψ are much higher than the inner peaks, and the highest probability density is near the classical turning points of the motion, as is true for the classical probability density graphed above. This is in accord with the correspondence principle. 4.19 For x ≥ 0, the Hamiltonian operator is the same as that of the harmonic oscillator. Hence the solutions of the Schrödinger equation for x ≥ 0 are the functions (4.42), where the coefficients obey the recursion relation (4.39). To make ψ quadratically integrable, ψ must go to zero as x → ∞. This boundary condition then restricts the solutions to the harmonic-oscillator functions (4.47). Since V is infinite for x < 0 , ψ must be zero for x < 0 (as for the particle in a box). The condition that ψ be continuous then requires that ψ = 0 at x = 0. The even harmonic-oscillator functions in (4.47) are not zero at the origin, so these are eliminated. Hence the well-behaved solutions are the harmonic oscillator wave functions with 1, 3, 5,., v = and 1 2 E h = + ( ) v ν with 1, 3, 5,. v = If we define n ≡ − ( 1)/2 v , then 3 2 E nh = + (2 ) ν , with n = 0, 1, 2,. 4.20 (a) The time-independent Schrödinger equation (3.47) is 2 2 22 22 2 2 2 2 11 1 22 2 ( /2 )( / / / ) ( ) . − ∂ ∂ +∂ ∂ +∂ ∂ + + + = m x y z kx ky kz E ψ ψ ψ ψψ xyz = The Hamiltonian operator is the sum of terms that each involve only one coordinate, so we try a separation of variables, taking ψ = f ( ) ( ) ( ). xg yhz Substitution of this ψ into the Schrödinger equation followed by division by fgh gives 22 2 2 11 1 2 22 2 22 22 2 ( ) 2 xyz d f dg dh gh f h fg k x k y k z fgh Efgh m dx dy dz ⎛ ⎞ − + + + ++ = ⎜ ⎟ ⎝ ⎠ = 22 2 2 11 1 2 22 2 22 22 2 1 11 2 xyz d f dg dh kx ky kz E mf g h dx dy dz ⎛ ⎞ − + + +++= ⎜ ⎟ ⎝ ⎠ = (Eq. 1) 22 2 2 2 1 11 2 22 2 22 2 22 1 11 2 2 x x yz d f dg dh E kx E ky kz mf m g h dx dy dz ⎛ ⎞ ≡− + = + + − − ⎜ ⎟ ⎝ ⎠ = = (Eq. 2) Since f is a function of x only, the defined quantity Ex is independent of y and z. Since Ex equals the right side of the last equation and x does not appear on this side, Ex is independent of x. Therefore Ex is a constant. Multiplication of the Ex definition by f gives 2 22 2 1 2 ( /2 )( / ) − += m d f dx k x f E f x x = , which is the same as the one-dimensional harmonic-oscillator (ho) Schrödinger equation (4.32) [see also (4.26)] with ψ replaced by f, k replaced by , x k and E replaced by Ex . Hence f(x) is the one-dimensional ho wave function (4.47) with v replaced by x v , and Ex is given by (4.45) and (4.23) as 1 1/2 2 ( ) , (1/2 )( / ) . E h km x x xx x =+ = v νν π Since x, y, and z occur symmetrically, g(y) and h(z) are ho functions with y and z as the variable. Equations 1 and 2 give

E=Es +Ey +E.=(Vx +)hx +(vy +hvy +(v:+)hv:.Where Vx=0,1,2.,V,=0,1,2.V=0,1,2, (b)When the k's are equal,we have vs=v=v:=v and E=(vx+v+v+hv.The lowest energy level is 000 and is nondegenerate,where the numbers give the values of the The next-lowest level is threefold degenerate, consisting of the states 100.010.and 001.The next level is sixfold degenerate and has the states 200,020,200,110,101,011.The next level is tenfold degenerate and has the states300030.003.111210201012021.102120 4.21(aH=(-l0°ee2=1.H1=(-10e'(d/d)e=-e(-2ze)=2z H2=e(-2e+4:2e)=4z2-2, h,=-e(4:e+8:e-82e)=823-12z (b)For n=0.Ho==andH==. Forn=l,h1=2:2ado+号h2=1+2:2-1=22 For n=2,H2=4:3-2:and 2H=4:+4:3-6:=423-2:. (c)For v,()is(/)as in (4.53).For v=1 (4.86)is =(2)2(aleax)=2V2xeas in(4.55).Finally, 2=(22.2)P(al)4eP[Max)-2]=2-V2(al)4(2ax-Dein as in (4.57). 4.22 For very large x,the first term in parentheses in(4.32)can be neglected compared with the second term.and (4.32)becomes w=0.With w=e,we have w-axy-aein+axen-axewin-aewin.For very largex large x. 4.23 (a)Let x =ax.Then Eq.(4.40)becomes w=e++线+s coacoa coa' Let E,mEh2/a=E/hv.Then Eq.(4.39)becomes cn2/ac =(2n+1-2E,)/[(n+)(n+2)]=,wheref was defined as shown.We e品=&品品-&品品品-6m 4-6 Copyright2014 Pearson Education.Inc
4-6 Copyright © 2014 Pearson Education, Inc. 111 222 ( ) ( ) ( ), EE E E h h h =++= + + + + + x yz x x y y z z vvv ν ν ν where 0, 1, 2, , 0, 1, 2, 0, 1, 2, v vv x yz = == . . (b) When the k’s are equal, we have ν xyz =ννν = ≡ and 3 2 ( ). E h = +++ vvv xyz ν The lowest energy level is 000 and is nondegenerate, where the numbers give the values of the quantum numbers , , . x y z vvv The next-lowest level is threefold degenerate, consisting of the states 100, 010, and 001. The next level is sixfold degenerate and has the states 200, 020, 200, 110, 101, 011. The next level is tenfold degenerate and has the states 300, 030, 003, 111, 210, 201, 012, 021, 102, 120. 4.21 (a) 2 2 0 0 ( 1) 1. z z H ee− =− = 2 22 2 1 ( 1) ( / ) ( 2 ) 2 . z zz z H e d dz e e ze z − − = − =− − = 22 2 2 2 2 ( 2 4 ) 4 2, zz z H e e ze z − − =− + =− 22 2 2 3 3 3 (4 8 8 ) 8 12 . zz z z H e ze ze z e z z −− − =− + − = − (b) For n = 0, 0 zH z = and 1 2 1 H z = . For n = 1, 2 1 zH z = 2 and 1 2 2 0 2 2 HH z z + =+ −= 12 12. For n = 2, 3 2 zH z z = − 4 2 and 1 3 3 1 3 2 2 4 4 6 4 2. H H zz zz z + =+ −= − (c) For 0, v = (4.86) is 2 1/4 /2 0 (/) , x e α ψ α π − = as in (4.53). For 1, v = (4.86) is 2 2 1/2 1/4 /2 1/2 1/2 3/4 1/4 /2 1 (2 1!) ( / ) (2 ) 2 x x e x xe α α ψ απ α α π − − −− =⋅ = , as in (4.55). Finally, 2 2 2 1/2 1/4 /2 1/2 2 1/2 1/4 2 /2 2 (2 2!) ( / ) [4( ) 2] 2 ( / ) (2 1) x x e x xe α α ψ απ α απ α −− − − = ⋅ −= − as in (4.57). 4.22 For very large | |, x the first term in parentheses in (4.32) can be neglected compared with the second term, and (4.32) becomes 2 2 ψ′′ −α ψx = 0. With 2 x /2 e α ψ − = , we have 2 2 22 2 2 /2 2 2 /2 2 2 /2 /2. x x xx x e xe xe e α α αα ψ αψ α α α α − − −− ′′ − =− + − =− For very large | |, x 2 x /2 e α α − − is extremely close to zero, so 2 x /2 e α ψ − = is an approximate solution for very large | | . x 4.23 (a) Let 1/2 r x ≡ α x . Then Eq. (4.40) becomes 2 2 4 6 /2 2 4 6 0 2 3 0 0 0 / 1 r x r r r cx cx c x c e c c c ψ α α α − ⎛ ⎞ = ++ ++ ⎜ ⎟ ⎝ ⎠ " Let 2 / / E mE E h r α ν − ≡ = = . Then Eq. (4.39) becomes 2 / (2 1 2 )/ [( 1)( 2)] nn r n c c n Enn f + α = +− + + ≡ , where nf was defined as shown. We have 2 4 42 42 6 6 0 20 420 2 3 0 20 420 0 0 , , c c cc cc c c f ff fff α αα ααα c cc ccc c c α α = == = = . . Hence

w1%=eP+6x+65x+65x+. We have2m-2=(4n-4+1-2E,)/M(2n-2+1(2n-2+2)=(4n-3-2E,)/(4n2-2m) A C++program is #include <iostream> #include <cmath> using namespace std; int main({ int n; double er,x灯,fac,sum,term,psi label2:cout <"Enter Er(enter 1000 to quit)"; cin>>er; if(er>999){ return 0; for (xr=0;xr<=6;xr=xr+0.5){ fac=exp(-xr"xr/2); sum=1; term=1; for(n=1;n<=9500;n=n+1){ term=term*(4*n-3-2*er)*xr*xr/(4*n*n-2*n); if(fabs(fac"term)<1e-15){ goto label1; } sum=sum+term: cout <<"Did not converge"; return 0; label1:psi=fac*sum; cout <<"xr ="<<xr <<"Psi="<psi <<"n="<n<<endl goto label2; } 4-7 Education.Inc
4-7 Copyright © 2014 Pearson Education, Inc. ( ) 2 /2 24 6 0 0 02 024 / 1 r x rr r ψ c e fx f fx f f fx − = ++ + +" . We have 2 2 2 (4 4 1 2 )/[(2 2 1)(2 2 2) (4 3 2 )/(4 2 ) nr r f n E n n n Enn − = − +− − + − + = −− − . A C++ program is #include <iostream> #include <cmath> using namespace std; int main () { int n; double er, xr, fac, sum, term, psi; label2: cout << "Enter Er (enter 1000 to quit)"; cin >> er; if (er > 999) { return 0; } for (xr=0; xr<=6; xr=xr+0.5) { fac=exp(-xr*xr/2); sum=1; term=1; for (n=1; n<=9500; n=n+1) { term=term*(4*n-3-2*er)*xr*xr/(4*n*n-2*n); if (fabs(fac*term) < 1e-15) { goto label1; } sum=sum+term; } cout << "Did not converge"; return 0; label1: psi=fac*sum; cout << " xr = " << xr << " Psi = " << psi << " n = " << n << endl; } goto label2; }