三、等温过程 dT=0, dE=0 Pi d迎r=dAr P2 ddr=pdv e-vr 0 0,=-rg=r安-a V pK,In P=pV,In P P2 P2 ∴.Ar= M P2 K
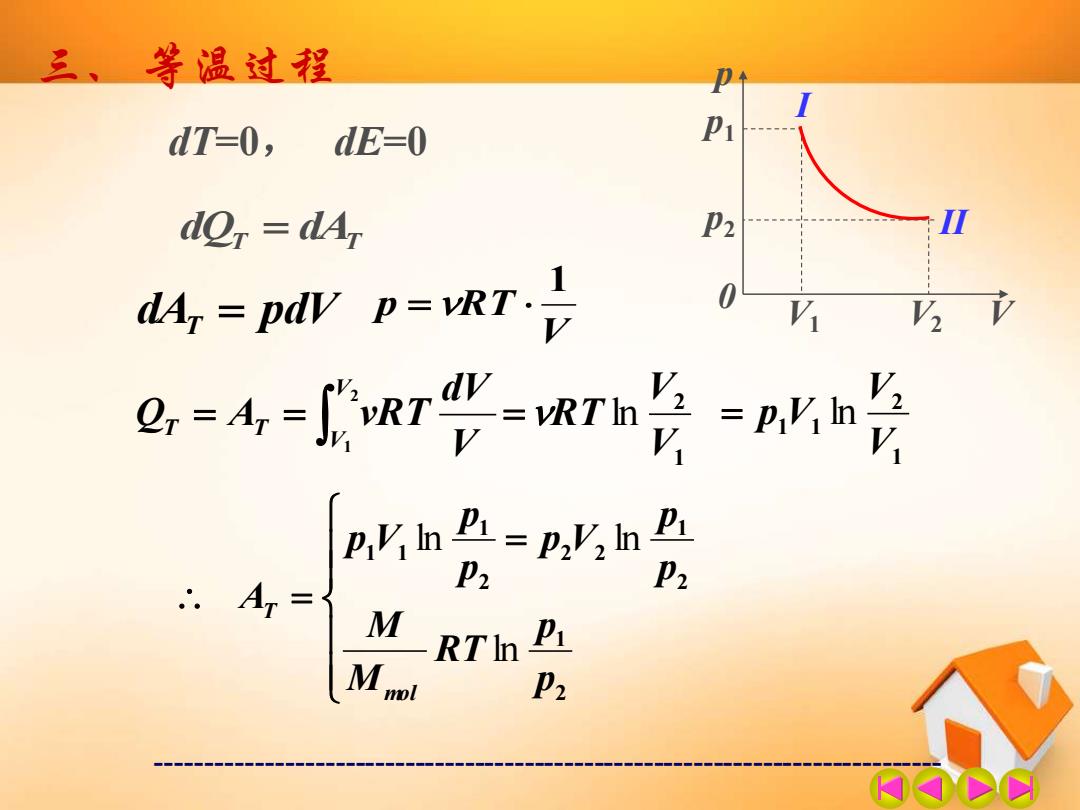
------------------------------------------------------------------------------- 三、 等温过程 p V1 V 0 p1 V2 I p2 II dT=0, dE=0 dQT = dAT dAT = pdV V p RT 1 = = = 2 1 V V T T V dV Q A vRT 1 2 V V =RT ln 1 2 1 1 V V = p V ln = = 2 1 2 1 2 2 2 1 1 1 p p RT M M p p p V p p p V A mol T ln ln ln

四、绝热过程 若系统状态变化过程中,系统与外界没有热交换. 特征 do =0 dE+d4=0 1.绝热方程 对于准静态过程有 vCrdT+pay =0 (10 PV=YRT 取微分得 pdy +Vdp vRdT (2) 由和2)逍去dT
------------------------------------------------------------------------------- 四、绝热过程 若系统状态变化过程中,系统与外界没有热交换. 特征 dQ = 0 dE+dA= 0 1.绝热方程 对于准静态过程有 vCV dT + pdV = 0 (1) pV = vRT 取微分得 pdV +Vdp = vRdT (2) 由(1)和(2)消去vdT

得 pdr+ap=-Rpd业 CypdV+CyVdp =-Rpdv CppdV+CvVφ=O p 上式积分 ∫华0 得 I p+yhV=C In pVr=C K CQ
------------------------------------------------------------------------------- 得 CV p V p V V p R d d + d = − CV pdV +CV Vdp = −RpdV CP pdV +CV Vdp = 0 + = 0 V dV p dp 上式积分 + = 0 V dV p dp 得 ln p + lnV = C pV = C ln
=C TVY-1=C2 p-1T-7=C3 一又称泊松方程 2.绝热线与等温线 P 绝热线 pV=C1,等温线 等温线 pVr=C2,绝热线 A(PAVA T) P O(P2V2 T) 对于等温过程 9(P3T) PV=C=PV i.p=
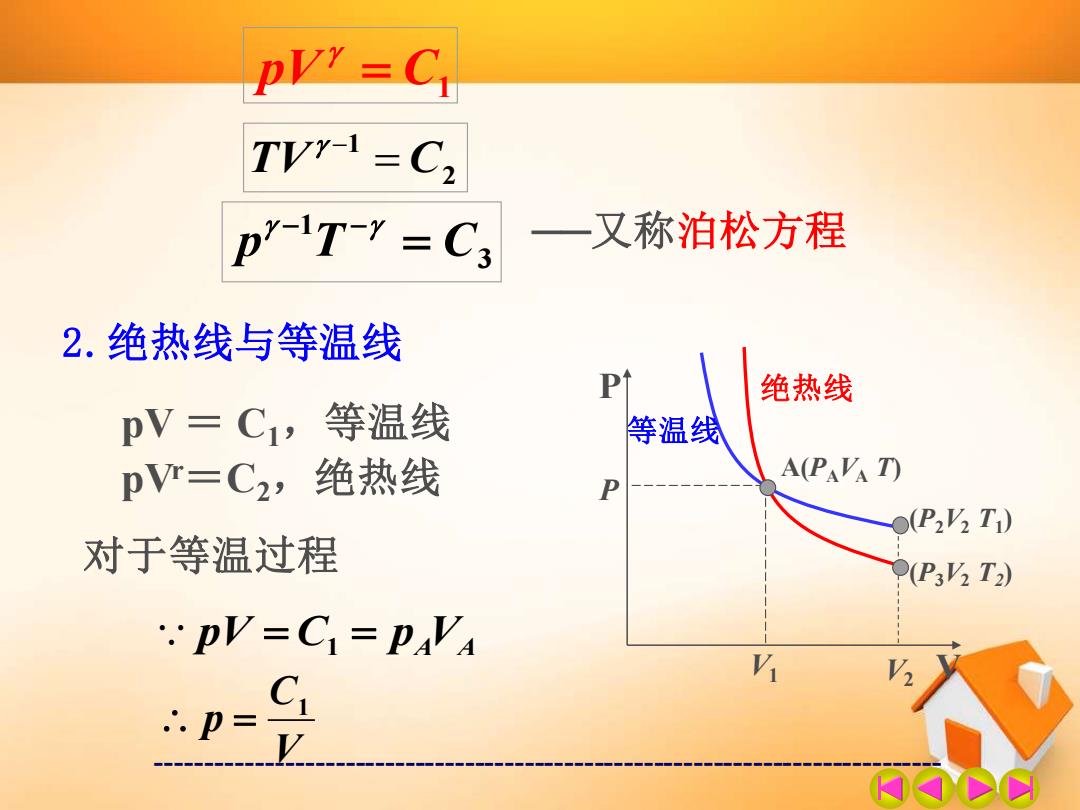
------------------------------------------------------------------------------- pV = C1 2 1 TV = C − 3 1 p T = C − − ──又称泊松方程 2.绝热线与等温线 pV = C1,等温线 pVr=C2,绝热线 P V A(PAVA T) 绝热线 等温线 (P2V2 T1 ) (P3V2 T2 ) V1 V2 P 对于等温过程 pV = C1 = pA VA V C p 1 =

你员收=是 对于绝热过程: 'pV'=C2=p' ∴p= dp PA Ay .y>1 >密 即绝热线要徒一些 K
------------------------------------------------------------------------------- 2 1 2 1 A AT A V C V C dV dp = − = − A A A A A V p V p V = − = − 2 对于绝热过程: A VA pV = C = p 2 V C p 2 = 1 1 2 + + = − = − A A A A A V p V V C dV dp A A V p = − ∵ > 1 A A A V p dV dp = A A AT V p dV dp = 即绝热线要徒一些