
菲涅耳衍射:障碍物离光源和考察点的距离都是有限的,或其中 之一的距离是有限的。也称近场衍射。 夫琅和费衍射:光源和考察点到障碍物的距离可以认为是无限远, 即实际上使用的是平行光束,又称远场衍射。较菲涅耳衍射更为 重要。 §2一3菲涅耳半波带 一.菲涅耳半波带 现以点光源为例说明惠一菲原理的应用。确定光波到达对称轴上 任一P点时波面S所起的作用。B称为P点对于波面的极点
⚫ 菲涅耳衍射:障碍物离光源和考察点的距离都是有限的,或其中 之一的距离是有限的。也称近场衍射。 ⚫ 夫琅和费衍射:光源和考察点到障碍物的距离可以认为是无限远, 即实际上使用的是平行光束,又称远场衍射。较菲涅耳衍射更为 重要。 §2—3 菲涅耳半波带 一. 菲涅耳半波带 ⚫ 现以点光源为例说明惠—菲原理的应用。确定光波到达对称轴上 任一P点时波面S所起的作用。 B0 称为P点对于波面的极点
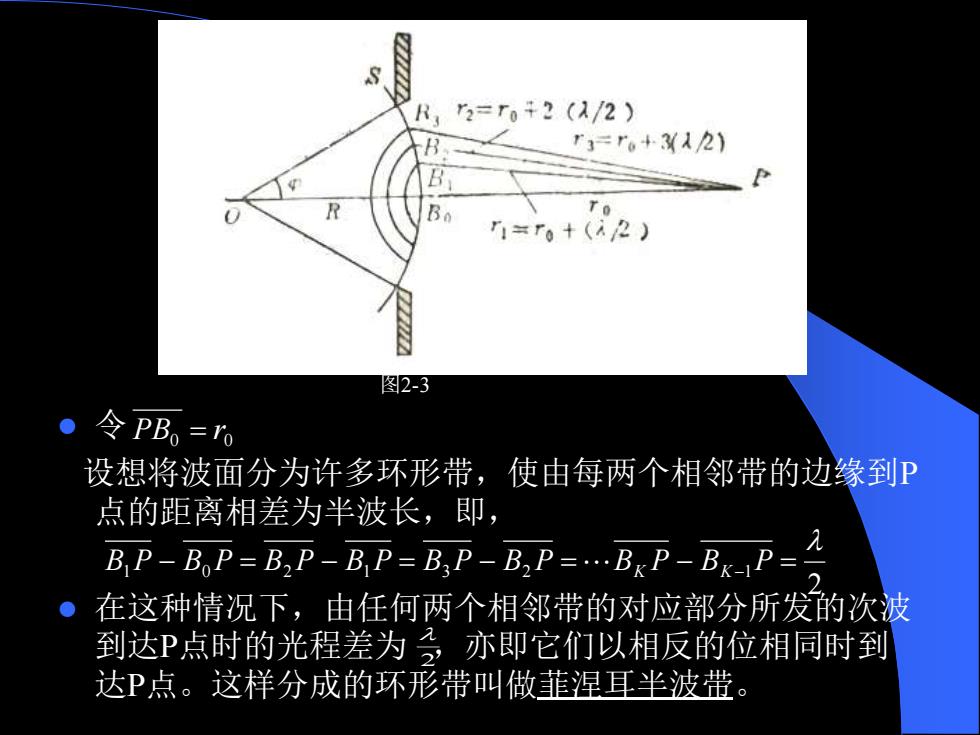
R,=rn+?(a/2) r3=r6+3X12) P R Bo T o =r。十(i2) 图2-3 o令PB。=r0 设想将波面分为许多环形带,使由每两个相邻带的边缘到P 点的距离相差为半波长,即, B.P-BoP=B:P-BP=B.P-B:P=.BkP-BkaP=4 在这种情况下,由任何两个相邻带的对应部分所发的次波 到达P点时的光程差为亦即它们以相反的位相同时到 达P点。这样分成的环形带叫做菲涅耳半波带
图2-3 ⚫ 令 设想将波面分为许多环形带,使由每两个相邻带的边缘到P 点的距离相差为半波长,即, ⚫ 在这种情况下,由任何两个相邻带的对应部分所发的次波 到达P点时的光程差为 ,亦即它们以相反的位相同时到 达P点。这样分成的环形带叫做菲涅耳半波带。 0 0 PB = r 2 1 0 2 1 3 2 1 B P − B P = B P − B P = B P − B P =BK P − BK− P = 2

二、合振幅的计算 以a1,a2·,窈别表示各半波带发出的次波在P点所产生的振幅,k 个半波带所发次波到达P点时叠加的结果,其合振幅为Ak A4=a41-a2+a3-a4+a5+t(-l)+ak R 图2-4
二、合振幅的计算 ⚫ 以 分别表示各半波带发出的次波在P点所产生的振幅,k 个半波带所发次波到达P点时叠加的结果,其合振幅 为 a a ak , , 1 2 Ak k k Ak a a a a a a 1 1 2 3 4 5 ( 1) + = − + − + ++ − 图2-4

按惠一菲原理: ak ok(0k) △S △S 为了计算 我们看下面的球冠,其面积为 S=2R.R(1-cos)=2R2 (1-cos) 而 R2+(R+)2- cOS= 2R(R+%) 将上列两式分别微分,得 ds=2πR2 sin od0 rdr sin od R(R+To) 则 ds 2πR R+ro
按惠—菲原理: 为了计算 ,我们看下面的球冠,其面积为 而 将上列两式分别微分,得 则 k k k k r S a k ( ) k k r S 2 (1 cos ) 2 (1 cos ) 2 S = R R − = R − 2 ( ) ( ) cos 0 2 2 0 2 R R r R R r rk + + + − = ( ) sin 2 sin 0 2 R R r r dr d ds R d k k + = = k k dr R r R r ds 0 2 + =
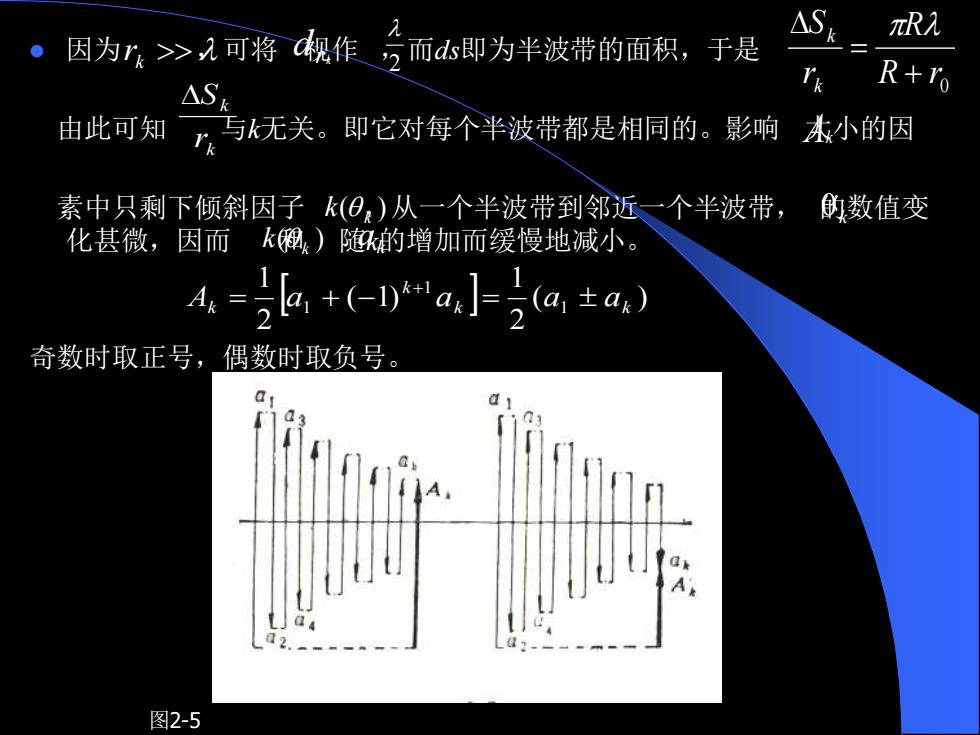
△SE R入 0 因为r>入可将视作2而ds即为半波带的面积,于是 △S r R+ro 由此可知 与无关。即它对每个半波带都是相同的。影响 本小的因 素中只剩下倾斜因子k(⊙)从一个半波带到邻近一个半波带, 的数值变 化甚微,因而k)随的增加而缓慢地减小。 4.=+-)"a小2a±a〉 奇数时取正号,偶数时取负号。 0 1 图2-5
⚫ 因为 ,可将 视作 ,而ds即为半波带的面积,于是 由此可知 与k无关。即它对每个半波带都是相同的。影响 大小的因 素中只剩下倾斜因子 ,从一个半波带到邻近一个半波带, 的数值变 化甚微,因而 和 随k的增加而缓慢地减小。 奇数时取正号,偶数时取负号。 rk drk 2 0 R r R r S k k + = k k r S Ak ( ) k k k ( ) k k ak ( ) 2 1 ( 1) 2 1 1 1 1 k k k Ak = a + − a = a a + 图2-5