
Be careful with the sample space ■ One should choose an appropriate sample space. Different elements of the sample space should be distinct and mutually exclusive,so that when the experiment is carried out there is a unique outcome. The sample space must also be collectively exhaustive,in the sense that no matter what happens in the experiment,we always obtain an outcome that has been included in the sample space
Be careful with the sample space One should choose an appropriate sample space. Different elements of the sample space should be distinct and mutually exclusive, so that when the experiment is carried out there is a unique outcome. The sample space must also be collectively exhaustive, in the sense that no matter what happens in the experiment, we always obtain an outcome that has been included in the sample space

Sequential models Many experiments have an inherently sequential character. Examples: tossing a coin three times, 0 observing the value of a stock on 5 successive days, receiving eight successive digits at a communication receiver. It is then often useful to describe the experiment and the associated sample space by means of a tree-based sequential description
Sequential models Many experiments have an inherently sequential character. Examples: tossing a coin three times, observing the value of a stock on 5 successive days, receiving eight successive digits at a communication receiver. It is then often useful to describe the experiment and the associated sample space by means of a tree-based sequential description
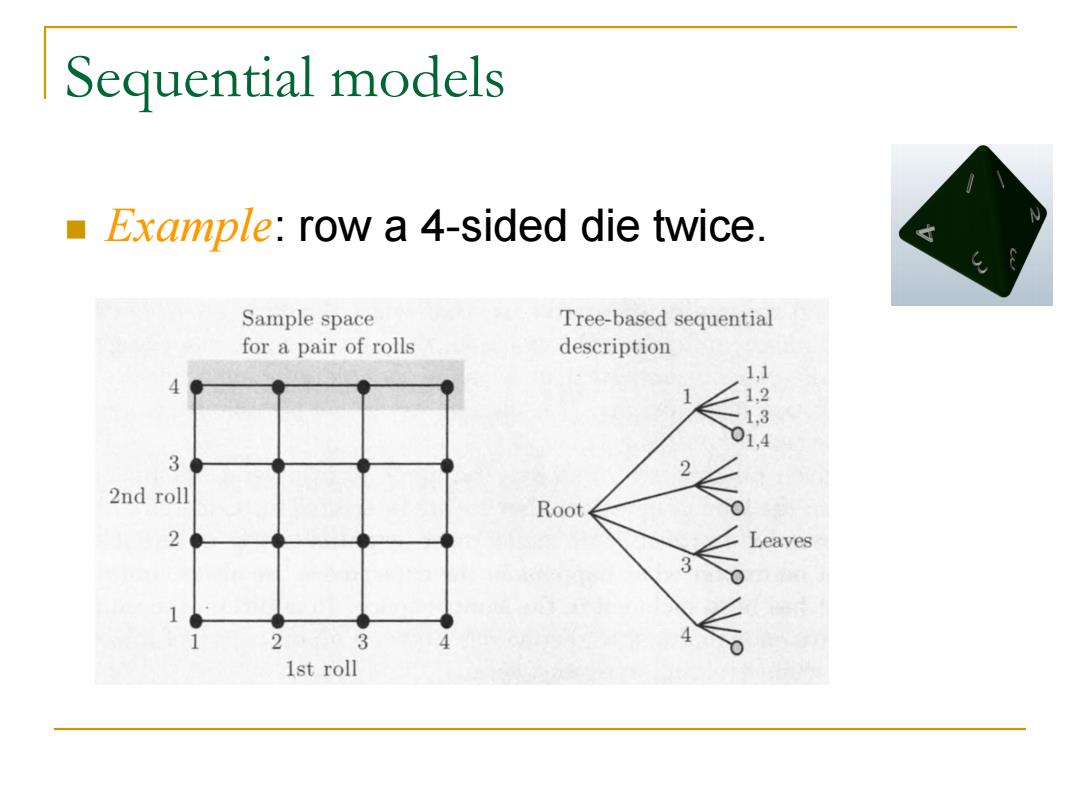
Sequential models Example:row a 4-sided die twice. Sample space Tree-based sequential for a pair of rolls description 1,1 4 1 1.2 1.3 01,4 3 2 2nd roll Root 2 Leaves 3 1 1 2 3 4 1st roll
Sequential models Example: row a 4-sided die twice

Probabilistic laws After we settled on the sample space n associated with an experiment,we need to introduce a probabilistic law. The probability law assigns to a set A of possible outcomes a nonnegative number P(A). The value P(A)encodes our knowledge or belief about the collective "likelihood"of the elements of A
Probabilistic laws After we settled on the sample space Ω associated with an experiment, we need to introduce a probabilistic law. The probability law assigns to a set 𝐴 of possible outcomes a nonnegative number 𝑃 𝐴 . The value 𝑃 𝐴 encodes our knowledge or belief about the collective "likelihood" of the elements of 𝐴

Probabilistic laws Consider the example of tossing two coins. What's P(HH)?P(HT)?P(TH)?P(TT)? Many possibilities.For example,uniform distribution says the following: P(HH)=P(HT)=P(TH)=P(TT)=1/4. For A =HH,TT,what's P(A)? In uniform distribution,P(A)=1/2
Probabilistic laws Consider the example of tossing two coins. What’s 𝑃 𝐻𝐻 ? 𝑃 𝐻𝑇 ? 𝑃 𝑇𝐻 ? 𝑃 𝑇𝑇 ? Many possibilities. For example, uniform distribution says the following: 𝑃 𝐻𝐻 = 𝑃 𝐻𝑇 = 𝑃 𝑇𝐻 = 𝑃 𝑇𝑇 = 1/4. For 𝐴 = 𝐻𝐻, 𝑇𝑇 , what’s 𝑃(𝐴)? In uniform distribution, 𝑃 𝐴 = 1/2