智能系统：改进教与学优化算法的LQR控制器优化设计

第9卷第5期 智能系统学报 Vol.9 No.5 2014年10月 CAAI Transactions on Intelligent Systems 0ct.2014 D0:10.3969/j.issn.1673-4785.201304071 改进教与学优化算法的LQR控制器优化设计 拓守恒，邓方安，雍龙泉 (陕西理工学院数学与计算机科学学院，陕西西安723000) 摘要：为了快速有效地确定线性二次最优控制(linear quadratic regulator,LQR)问题中的加权矩阵Q和R,针对主 动悬架LQR控制器权系数设计问题，提出一种改进的教与学优化算法进行LQR优化设计。算法对基本教与学优化 算法中的“教”与“学”阶段进行了进一步的改进，同时提出一种“自我学习”策略。通过仿真实验表明，和基本教与 学算法、粒子群算法、遗传算法相比，本文算法在对主动悬架QR控制器优化时，具有收敛速度快，求解精度高和稳 定性强等优势。 关键词：教与学优化算法；LQR控制器：优化控制：主动悬架：粒子群优化算法：遗传算法 中图分类号：TP18文献标志码：A文章编号：1673-4785(2014)05-0602-06 中文引用格式：拓守恒，邓方安，雍龙泉.改进教与学优化算法的LQ控制器优化设计[J].智能系统学报，2014,9(5)：602-607. 英文引用格式：TUO Shouheng,DENG Fang'an,YONG Longquan.Optimal design of a linear quadratic regulator(LQR)control- ler based on the modified teaching-learning-based optimization algorithm[J].CAAI Transactions on Intelligent Systems,2014,9 (5):602-607. Optimal design of a linear quadratic regulator (LQR)controller based on the modified teaching-learning-based optimization algorithm TUO Shouheng,DENG Fang'an,YONG Longquan (School of Mathematics and Computer Science,Shaanxi University of Technology,XI'an 723000,China) Abstract:To determine the weighting matrix O and R for a linear quadratic regulator(LQR),a modified teaching- learning-based optimization (MTLBO)algorithm is proposed to tune weighting factors for active suspension LOR controller.The "Teaching"phase and "learning"phase are modified using MTLBO based on the basic TLBO algo- rithm.A novel"self-learning"strategy is employed in MTLBO.The simulation results showed that the MTLBO algo- rithm has distinct advantages in convergence,precision and stability than basic TLBO,PSO and genetic algorithms. Keywords:teaching-learning-based optimization algorithm;LOR controller;optimal control;active suspension; particle swarm optimization;genetic algorithm 线性二次最优控制(linear quadratic regulator, 在实际应用中，在进行LQR控制器的设计时， LQR))在现在的控制理论中是一种非常重要的最 关键问题是对权矩阵Q和R的调整，Q和R的选取 优控制算法，这主要是由于LQR是其他控制方法的 往往和所设计的控制器有关，并且没有好的方法确 基础并且能够很容易地应用到工程控制问题中。目 定Q和R。设计者往往凭经验采用多次试探法来 前，LQR控制方法已经广泛应用于异步电动机控 确定一种相对较好的Q和R,但是，试探法往往得 制、车辆驱动轴控制和结构振动控制等方面。 到的是局部最优控制方法。为此，Kalman首先提出 一种加权矩阵选择法2。文献[3]对加权矩阵选择 收稿日期：2013-04-24 基金项目：国家自然科学基金资助项目(11401357)：陕西省教育厅基金 法进行了进一步的改进。近年来，研究者采用遗传 资助项目(14K1141):汉中市科技局基金资助项目 (2013hzx-39). 算法[4】、粒子群算法[8】和蚁群算法[等群智能算 通信作者：拓守恒.uo_sh@126.com. 法进行LQR控制器的优化并取得不错效果。但是

第 ９ 卷第 ５ 期 智 能 系 统 学 报 Ｖｏｌ．９ №．５ ２０１４ 年 １０ 月 ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ Ｏｃｔ． ２０１４ ＤＯＩ：１０．３９６９ ／ ｊ．ｉｓｓｎ．１６７３⁃４７８５．２０１３０４０７１ 改进教与学优化算法的 ＬＱＲ 控制器优化设计 拓守恒，邓方安，雍龙泉 （陕西理工学院 数学与计算机科学学院，陕西 西安 ７２３０００ ） 摘 要：为了快速有效地确定线性二次最优控制（ｌｉｎｅａｒ ｑｕａｄｒａｔｉｃ ｒｅｇｕｌａｔｏｒ， ＬＱＲ）问题中的加权矩阵 Ｑ 和 Ｒ，针对主 动悬架 ＬＱＲ 控制器权系数设计问题，提出一种改进的教与学优化算法进行 ＬＱＲ 优化设计。 算法对基本教与学优化 算法中的“教”与“学”阶段进行了进一步的改进，同时提出一种“自我学习”策略。 通过仿真实验表明，和基本教与 学算法、粒子群算法、遗传算法相比，本文算法在对主动悬架 ＬＱＲ 控制器优化时，具有收敛速度快，求解精度高和稳 定性强等优势。 关键词：教与学优化算法；ＬＱＲ 控制器； 优化控制； 主动悬架； 粒子群优化算法；遗传算法 中图分类号： ＴＰ１８ 文献标志码：Ａ 文章编号：１６７３⁃４７８５（２０１４）０５⁃０６０２⁃０６ 中文引用格式：拓守恒，邓方安，雍龙泉． 改进教与学优化算法的 ＬＱＲ 控制器优化设计［Ｊ］． 智能系统学报， ２０１４， ９（５）： ６０２⁃６０７． 英文引用格式：ＴＵＯ Ｓｈｏｕｈｅｎｇ，ＤＥＮＧ Ｆａｎｇ’ａｎ，ＹＯＮＧ Ｌｏｎｇｑｕａｎ． Ｏｐｔｉｍａｌ ｄｅｓｉｇｎ ｏｆ ａ ｌｉｎｅａｒ ｑｕａｄｒａｔｉｃ ｒｅｇｕｌａｔｏｒ （ＬＱＲ） ｃｏｎｔｒｏｌ⁃ ｌｅｒ ｂａｓｅｄ ｏｎ ｔｈｅ ｍｏｄｉｆｉｅｄ ｔｅａｃｈｉｎｇ⁃ｌｅａｒｎｉｎｇ⁃ｂａｓｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ ａｌｇｏｒｉｔｈｍ［ Ｊ］． ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ， ２０１４， ９ （５）： ６０２⁃６０７． Ｏｐｔｉｍａｌ ｄｅｓｉｇｎ ｏｆ ａ ｌｉｎｅａｒ ｑｕａｄｒａｔｉｃ ｒｅｇｕｌａｔｏｒ （ＬＱＲ） ｃｏｎｔｒｏｌｌｅｒ ｂａｓｅｄ ｏｎ ｔｈｅ ｍｏｄｉｆｉｅｄ ｔｅａｃｈｉｎｇ⁃ｌｅａｒｎｉｎｇ⁃ｂａｓｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ ａｌｇｏｒｉｔｈｍ ＴＵＯ Ｓｈｏｕｈｅｎｇ， ＤＥＮＧ Ｆａｎｇ’ａｎ， ＹＯＮＧ Ｌｏｎｇｑｕａｎ （Ｓｃｈｏｏｌ ｏｆ Ｍａｔｈｅｍａｔｉｃｓ ａｎｄ Ｃｏｍｐｕｔｅｒ Ｓｃｉｅｎｃｅ， Ｓｈａａｎｘｉ Ｕｎｉｖｅｒｓｉｔｙ ｏｆ Ｔｅｃｈｎｏｌｏｇｙ， ＸＩ′ａｎ ７２３０００， Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｔｏ ｄｅｔｅｒｍｉｎｅ ｔｈｅ ｗｅｉｇｈｔｉｎｇ ｍａｔｒｉｘ Ｑ ａｎｄ Ｒ ｆｏｒ ａ ｌｉｎｅａｒ ｑｕａｄｒａｔｉｃ ｒｅｇｕｌａｔｏｒ （ＬＱＲ）， ａ ｍｏｄｉｆｉｅｄ ｔｅａｃｈｉｎｇ⁃ ｌｅａｒｎｉｎｇ⁃ｂａｓｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ （ＭＴＬＢＯ） ａｌｇｏｒｉｔｈｍ ｉｓ ｐｒｏｐｏｓｅｄ ｔｏ ｔｕｎｅ ｗｅｉｇｈｔｉｎｇ ｆａｃｔｏｒｓ ｆｏｒ ａｃｔｉｖｅ ｓｕｓｐｅｎｓｉｏｎ ＬＱＲ ｃｏｎｔｒｏｌｌｅｒ． Ｔｈｅ “Ｔｅａｃｈｉｎｇ” ｐｈａｓｅ ａｎｄ “ｌｅａｒｎｉｎｇ” ｐｈａｓｅ ａｒｅ ｍｏｄｉｆｉｅｄ ｕｓｉｎｇ ＭＴＬＢＯ ｂａｓｅｄ ｏｎ ｔｈｅ ｂａｓｉｃ ＴＬＢＯ ａｌｇｏ⁃ ｒｉｔｈｍ． Ａ ｎｏｖｅｌ “ｓｅｌｆ⁃ｌｅａｒｎｉｎｇ” ｓｔｒａｔｅｇｙ ｉｓ ｅｍｐｌｏｙｅｄ ｉｎ ＭＴＬＢＯ． Ｔｈｅ ｓｉｍｕｌａｔｉｏｎ ｒｅｓｕｌｔｓ ｓｈｏｗｅｄ ｔｈａｔ ｔｈｅ ＭＴＬＢＯ ａｌｇｏ⁃ ｒｉｔｈｍ ｈａｓ ｄｉｓｔｉｎｃｔ ａｄｖａｎｔａｇｅｓ ｉｎ ｃｏｎｖｅｒｇｅｎｃｅ， ｐｒｅｃｉｓｉｏｎ ａｎｄ ｓｔａｂｉｌｉｔｙ ｔｈａｎ ｂａｓｉｃ ＴＬＢＯ， ＰＳＯ ａｎｄ ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍｓ． Ｋｅｙｗｏｒｄｓ：ｔｅａｃｈｉｎｇ⁃ｌｅａｒｎｉｎｇ⁃ｂａｓｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ ａｌｇｏｒｉｔｈｍ； ＬＱＲ ｃｏｎｔｒｏｌｌｅｒ； ｏｐｔｉｍａｌ ｃｏｎｔｒｏｌ； ａｃｔｉｖｅ ｓｕｓｐｅｎｓｉｏｎ； ｐａｒｔｉｃｌｅ ｓｗａｒｍ ｏｐｔｉｍｉｚａｔｉｏｎ； ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ 收稿日期：２０１３⁃０４⁃２４． 基金项目：国家自然科学基金资助项目（１１４０１３５７）；陕西省教育厅基金 资助 项 目 （ １４ＪＫ１１４１ ）； 汉 中 市 科 技 局 基 金 资 助 项 目 （２０１３ｈｚｚｘ⁃３９）． 通信作者：拓守恒．ｔｕｏ＿ｓｈ＠ １２６．ｃｏｍ． 线性二次最优控制（ ｌｉｎｅａｒ ｑｕａｄｒａｔｉｃ ｒｅｇｕｌａｔｏｒ， ＬＱＲ） ［１］在现在的控制理论中是一种非常重要的最 优控制算法，这主要是由于 ＬＱＲ 是其他控制方法的 基础并且能够很容易地应用到工程控制问题中。 目 前，ＬＱＲ 控制方法已经广泛应用于异步电动机控 制、车辆驱动轴控制和结构振动控制等方面。 在实际应用中，在进行 ＬＱＲ 控制器的设计时， 关键问题是对权矩阵 Ｑ 和 Ｒ 的调整，Ｑ 和 Ｒ 的选取 往往和所设计的控制器有关，并且没有好的方法确 定 Ｑ 和 Ｒ。 设计者往往凭经验采用多次试探法来 确定一种相对较好的 Ｑ 和 Ｒ，但是，试探法往往得 到的是局部最优控制方法。 为此，Ｋａｌｍａｎ 首先提出 一种加权矩阵选择法［２］ 。 文献［３］对加权矩阵选择 法进行了进一步的改进。 近年来，研究者采用遗传 算法［４⁃７］ 、粒子群算法［８］ 和蚁群算法［９］ 等群智能算 法进行 ＬＱＲ 控制器的优化并取得不错效果。 但是

第5期 拓守恒，等：改进教与学优化算法的LQR控制器优化设计 ·603. 还是存在优化用时长、获得全局最优解成功率低等 在标准的TLB0算法中，“班级”是个体的集合， 问题1山，本文提出一种改进的教与学优化算法进 每个个体相当于一个学员，每个学员所学的某一科 行LQR控制器的优化。 目相当于一个决策变量。水平最高的学员被称为 “教师”。每个学员通过“教师”的“教”和向其他学 1 LQR控制算法 员“学习”来提高自身水平。 假设受控线性不变系统的状态方程模型为 1)“教”阶段。 在“教”阶段，班级中每个学员(j=1,2,… x()=Ax(t)+Bu(t） (1) NP)根据Xeer和班级中学员平均水平值Mean= y(t)=Cx(t)+Du(t) 式中：x(t)是状态向量，u(t)是控制向量，y(t)是 三：之间的差异性进行学习。教学过程如下： 输出向量，A是系数矩阵，B是输入矩阵，C是输出 Xm=Xld Difference 矩阵，D是传递矩阵。 Difference=T:·(X,eaha-Tf:·Mean) 定义控制系统的二次型性能泛函为 式中：X表示第i个学员学习前的值，X表示第i个 Jsx+ros+aR1出 (2) 学员学习后的值，TF:=round[1+rand(0,l)]是教学 因子，：∈U(0,1)是随机学习步长，表示学习速率。 式中：Q为状态变量的加权矩阵，是半正定矩阵；R 2)“学”阶段 为输入变量的加权矩阵，是正定矩阵。 在“学”阶段，学员X(i=1,2,…,NP)从班级 该系统最优控制的目标是寻求最优控制(t), 中随机选取一个学员”(=1,2，…，NP,j≠)作为 使得系统趋近于初始化状态，并使J取得最小值。 学习对象，X分析和比较自己和学员？之间的差 由线性二次型最优控制理论可知，如果要使得J最 异，然后进行学习。学习过程如下： 小，则控制向量应该为 Xaa+r:·(X'-),f)<fX) u(t)=RB'Px (3) X.= 式中：P为对称矩阵，该矩阵满足： X+r·(N-X),fX)<f) 式中，：=U(0,1)表示第i个学员的学习因子（学 P=-PA -AP PBR-BP-O (4) 习步长)。 考虑在稳态的情况下，系统状态逐渐趋近于0，可将 3)学习结果更新，学员在经过学习后要进行更 式(4)简化为Riccati代数方程： 新操作。更新方法如下： PA +A'P-PBRB'P+O=0 (5) IF is better than 显然，上述最优控制系统的性能指标主要取决于对 =he 称矩阵P,而P主要由矩阵A、B、Q和R确定。A和 End IF B是参数矩阵，因此，系统性能主要由矩阵Q和R 基本TLBO算法的流程如图1所示。 来决定。然而，Q和R怎样选取没有具体的求解方 法，常常依赖于设计者的主观经验进行实验调整，直 3改进的教与学优化算法 至获得相对可接受的满意解。 在标准的TLBO算法中，所有学员的的水平提 本文采用一种新型改进快速智能优化算法进行 高，完全依赖老师的“教”和学员之间的交流“学 LQR控制器的优化设计。通过汽车主动悬架作为 习”，从而使得学员在学习过程中对他人的过度依 被控对象，将提出的一种新的“教与学”优化算法应 赖。我们知道，每个人的学习主要是靠自身的努力 用于LQR控制器的设计中，并将结果与遗传算法、 和探索，个人的创新能力是最重要的19-0)。因此， 粒子群优化算法和标准的“教与学”优化算法在 为了发挥群体中每个学员的创新能力，本文提出一 LQR控制器优化中的性能进行比较。 种具有自我学习能力的教与学优化算法(motified 2教与学优化算法 teaching-learning-based optimization,MTLBO), 借鉴和声搜索算法思想进行个体的自我学习和自我 “教与学”优化(TLB0)算法[2-11是一种新型的 探索创新能力挖掘，用于加强每个个体的局部搜索 群体智能优化算法，通过模拟人类的学习过程： 能力，从而增强种群的全局最优解的求解能力。 “教”和“学”。通过两个阶段的学习，从而促进每个 3.1“教”(Teaching)学阶段的改进 个体的学习水平。 本文中对Mean进行改进，使的原来的Mean=

还是存在优化用时长、获得全局最优解成功率低等 问题［１０⁃１１］ ，本文提出一种改进的教与学优化算法进 行 ＬＱＲ 控制器的优化。 １ ＬＱＲ 控制算法 假设受控线性不变系统的状态方程模型为 ｘ · （ｔ） ＝ Ａｘ（ｔ） ＋ Ｂｕ（ｔ） ｙ（ｔ） ＝ Ｃｘ（ｔ） ＋ Ｄｕ（ｔ） { （１） 式中： ｘ（ｔ） 是状态向量， ｕ（ｔ） 是控制向量， ｙ（ｔ） 是 输出向量，Ａ 是系数矩阵，Ｂ 是输入矩阵，Ｃ 是输出 矩阵，Ｄ 是传递矩阵。 定义控制系统的二次型性能泛函为 Ｊ ＝ １ ２ ｘ Ｔ Ｓｘ ＋ １ ２ ∫ ｔ ｆ ｔ０ ｘ ＴＱｘ ＋ ｕ Ｔ [ Ｒｕ] ｄｔ （２） 式中：Ｑ 为状态变量的加权矩阵，是半正定矩阵；Ｒ 为输入变量的加权矩阵，是正定矩阵。 该系统最优控制的目标是寻求最优控制 ｕ（ｔ） ， 使得系统趋近于初始化状态，并使 Ｊ 取得最小值。 由线性二次型最优控制理论可知，如果要使得 Ｊ 最 小，则控制向量应该为 ｕ ∗ （ｔ） ＝ Ｒ ⁃１Ｂ ＴＰｘ （３） 式中：Ｐ 为对称矩阵，该矩阵满足： Ｐ · ＝ － ＰＡ － Ａ ＴＰ ＋ ＰＢＲ －１Ｂ ＴＰ － Ｑ （４） 考虑在稳态的情况下，系统状态逐渐趋近于 ０，可将 式（４）简化为 Ｒｉｃｃａｔｉ 代数方程： ＰＡ ＋ Ａ ＴＰ － ＰＢＲ －１Ｂ ＴＰ ＋ Ｑ ＝ ０ （５） 显然，上述最优控制系统的性能指标主要取决于对 称矩阵 Ｐ，而 Ｐ 主要由矩阵 Ａ、Ｂ、Ｑ 和 Ｒ 确定。 Ａ 和 Ｂ 是参数矩阵，因此，系统性能主要由矩阵 Ｑ 和 Ｒ 来决定。 然而，Ｑ 和 Ｒ 怎样选取没有具体的求解方 法，常常依赖于设计者的主观经验进行实验调整，直 至获得相对可接受的满意解。 本文采用一种新型改进快速智能优化算法进行 ＬＱＲ 控制器的优化设计。 通过汽车主动悬架作为 被控对象，将提出的一种新的“教与学”优化算法应 用于 ＬＱＲ 控制器的设计中，并将结果与遗传算法、 粒子群优化算法和标准的“ 教与学” 优化算法在 ＬＱＲ 控制器优化中的性能进行比较。 ２ 教与学优化算法 “教与学”优化（ＴＬＢＯ）算法［１２－１８］是一种新型的 群体智能优化算法， 通过模拟人类的学习过程： “教”和“学”。 通过两个阶段的学习，从而促进每个 个体的学习水平。 在标准的 ＴＬＢＯ 算法中，“班级”是个体的集合， 每个个体相当于一个学员，每个学员所学的某一科 目相当于一个决策变量。 水平最高的学员被称为 “教师”。 每个学员通过“教师”的“教”和向其他学 员“学习”来提高自身水平。 １） “教”阶段。 在“教”阶段，班级中每个学员 Ｘ ｊ （ ｊ ＝ １，２，…， ＮＰ） 根据 Ｘｔｅａｃｈｅｒ 和班级中学员平均水平值 Ｍｅａｎ ＝ １ ＮＰ∑ ＮＰ ｉ ＝ １ Ｘ ｉ 之间的差异性进行学习。 教学过程如下： Ｘ ｉ ｎｅｗ ＝ Ｘ ｉ ｏｌｄ ＋ Ｄｉｆｆｅｒｅｎｃｅ Ｄｉｆｆｅｒｅｎｃｅ ＝ ｒｉ·（Ｘｔｅａｃｈｅｒ － ＴＦｉ·Ｍｅａｎ） 式中： Ｘ ｉ ｏｌｄ 表示第 ｉ 个学员学习前的值， Ｘ ｉ ｎｅｗ 表示第 ｉ 个 学员学习后的值， ＴＦｉ ＝ ｒｏｕｎｄ [１ ＋ ｒａｎｄ（０，１）] 是教学 因子， ｒｉ ∈∪ （０，１） 是随机学习步长，表示学习速率 。 ２）“学”阶段 在“学”阶段，学员 Ｘ ｉ （ｉ ＝ １，２，…，ＮＰ） 从班级 中随机选取一个学员 Ｘ ｊ （ｊ ＝ １，２，…，ＮＰ，ｊ≠ｉ） 作为 学习对象， Ｘ ｉ 分析和比较自己和学员 Ｘ ｊ 之间的差 异，然后进行学习。 学习过程如下： Ｘ ｉ ｎｅｗ ＝ Ｘ ｉ ｏｌｄ ＋ ｒｉ·（Ｘ ｉ － Ｘ ｊ ）， ｆ（Ｘ ｊ ） ＜ ｆ（Ｘ ｉ ） Ｘ ｉ ｏｌｄ ＋ ｒｉ·（Ｘ ｊ － Ｘ ｉ ）， ｆ（Ｘ ｉ ） ＜ ｆ（Ｘ ｊ { ） 式中， ｒｉ ＝ Ｕ（０，１） 表示第 ｉ 个学员的学习因子（学 习步长）。 ３）学习结果更新，学员在经过学习后要进行更 新操作。 更新方法如下： ＩＦ Ｘ ｉ ｎｅｗ ｉｓ ｂｅｔｔｅｒ ｔｈａｎ Ｘ ｉ ｏｌｄ Ｘ ｉ ＝ Ｘ ｉ ｎｅｗ Ｅｎｄ ＩＦ 基本 ＴＬＢＯ 算法的流程如图 １ 所示。 ３ 改进的教与学优化算法 在标准的 ＴＬＢＯ 算法中，所有学员的的水平提 高，完全依赖老师的“教” 和学员之间的交流“ 学 习”，从而使得学员在学习过程中对他人的过度依 赖。 我们知道，每个人的学习主要是靠自身的努力 和探索，个人的创新能力是最重要的［１９－２０］ 。 因此， 为了发挥群体中每个学员的创新能力，本文提出一 种具有自我学习能力的教与学优化算法（ ｍｏｔｉｆｉｅｄ ｔｅａｃｈｉｎｇ⁃ｌｅａｒｎｉｎｇ⁃ｂａｓｅｄ ｏｐｔｉｍｉｚａｔｉｏｎ， ＭＴＬＢＯ），算法 借鉴和声搜索算法思想进行个体的自我学习和自我 探索创新能力挖掘，用于加强每个个体的局部搜索 能力，从而增强种群的全局最优解的求解能力。 ３．１ “教”（Ｔｅａｃｈｉｎｇ）学阶段的改进 本文中对 Ｍｅａｎ 进行改进，使的原来的 Ｍｅａｎ ＝ 第 ５ 期 拓守恒，等：改进教与学优化算法的 ＬＱＲ 控制器优化设计 ·６０３·

·604. 智能系统学报 第9卷 (X+X)/2,这样计算的好处是每个个体X,在教 Select 2 individuals at random XX,,from the 学过程中Mean值都不同，从而保证种群的多样性， current population 避免算法过早收敛，具体如下： Iff(X,)<f(X) TF round [1 rand(1,d)] X,=2×X,-X2 Else X=X;rand(1,d).* (Xom+X:） X,=2×X2-X Te.* End 2 (i=1,2,…,d) X..=X,rand(1,d).x (X,-X) End (开始 rand(1,d)表示在[0,1]区间随机生成一个d 参数初始化 维的行向量。 3.3“自我”学习(self-learning)阶段 随机初始化种群 本文算法提出一种类似于和声搜索算法的自我 i=1 学习策略。每个个体通过自我调整进行优化学习。 X..=Yu+difference 由于每个学员可能同时学习多门课程（多个决策变 “教” 量)，在进行“自我”学习时只是对部分科目进行调 KXKKX 食 整学习，保持优势学科，增强劣势科目。采用3种自 我调整策略进行学习： X:-=Xnguu 1)向“某一科”较为优秀的同学学习，增强单科 从种群中随机挑取X(化) 水平。学习概率为LoP。 2)自我调整，以概率SRP进行科目调整，调整 N AXAX) 步长为Stepo 3)以概率LP进行创新学习。 学” X.w=Y+r (YX) Xm=r4tr,(X-X） 阶 “自我”学习阶段的具体算法如下： For i=1 to NP KXKX Xnew =Xi Y Forj=1 to d X=X If rand()<LoP X)=X0),a∈U以1,2，…，NP);/策略(1) Elself rand()<SRP Y <i≤NP> X.n)=X.)±rand(0,1)×Step()/策略(2) IN Elseif rand()<ILP 是否满足结束条件 X(0)=x()+and×(x'(G)-xt()）:/第略3) Y End 结束 End 图1TLBO算法流程图 End Fig.1 Flow chart of TLBO algorithm 其中， 3.2“学习”(Learning)阶段的改进 Step minStep (maxStep TLB0算法在相互“学习”阶段，每个学员X(i= 1,2,…,N)每次学习时随机选取一个学习对象 minStep) Xj=1,2,…,N,j≠i)进行学习，学习较为单一。 maxStep =(x-x)/50 本文算法要求每个学员在进行“相互学习”是，每次 minStep =(x)/3 000 从班级中随机选取2个学习对象X,和X2(1=1, t是当且迭代次数，T是允许最大迭代次数。 2,…,N;2=1,2,…,N;1≠2)进行学习，学习过 4. MTBO算法主动悬架LQR控制器优化 程伪代码如下： 4.1车辆主动悬架LQR控制器模型 For i=1:NP 本文以单轮车辆模型作为研究对象，如图2

（Ｘｗｏｒｓｔ ＋ Ｘｉ） ／ ２，这样计算的好处是每个个体 Ｘｉ 在教 学过程中 Ｍｅａｎ 值都不同，从而保证种群的多样性， 避免算法过早收敛，具体如下： ＴＦ ＝ ｒｏｕｎｄ [１ ＋ ｒａｎｄ(１，ｄ) ] Ｘｎｅｗ ＝ Ｘｉ ＋ ｒａｎｄ(１，ｄ) ．∗ Ｘｔｅａｃｈｅｒ － ＴＦ ．∗ Ｘｗｏｒｓｔ ＋ Ｘｉ ( ) ２ é ë ê ê êê ù û ú ú úú （ｉ ＝ １，２，…，ｄ） 图 １ ＴＬＢＯ 算法流程图 Ｆｉｇ．１ Ｆｌｏｗ ｃｈａｒｔ ｏｆ ＴＬＢＯ ａｌｇｏｒｉｔｈｍ ３．２ “学习”（Ｌｅａｒｎｉｎｇ）阶段的改进 ＴＬＢＯ 算法在相互“学习”阶段，每个学员 Ｘｉ（ｉ ＝ １，２，…，Ｎ） 每次学习时随机选取一个学习对象 Ｘｊ（ｊ ＝１，２，…，Ｎ，ｊ ≠ ｉ） 进行学习，学习较为单一。 本文算法要求每个学员在进行“相互学习”是，每次 从班级中随机选取 ２ 个学习对象 Ｘｒ１ 和 Ｘｒ２ （ｒ１ ＝ １， ２，…，Ｎ；ｒ２ ＝ １，２，…，Ｎ；ｒ１ ≠ ｒ２ ） 进行学习，学习过 程伪代码如下： Ｆｏｒ ｉ ＝ １：ＮＰ Ｓｅｌｅｃｔ ２ ｉｎｄｉｖｉｄｕａｌｓ ａｔ ｒａｎｄｏｍ Ｘｒ１ ≠ Ｘｒ２ ｆｒｏｍ ｔｈｅ ｃｕｒｒｅｎｔ ｐｏｐｕｌａｔｉｏｎ Ｉｆ ｆ Ｘｒ１ ( ) ＜ ｆ Ｘｒ２ ( ) Ｘｒ ＝ ２ × Ｘｒ１ － Ｘｒ２ ； Ｅｌｓｅ Ｘｒ ＝ ２ × Ｘｒ２ － Ｘｒ１ ； Ｅｎｄ Ｘｎｅｗ ＝ Ｘｉ ＋ ｒａｎｄ(１，ｄ) ． × Ｘｒ － Ｘｉ ( ) ； Ｅｎｄ ｒａｎｄ（１， ｄ ）表示在［０，１］区间随机生成一个 ｄ 维的行向量。 ３．３“自我”学习（ｓｅｌｆ⁃ｌｅａｒｎｉｎｇ）阶段 本文算法提出一种类似于和声搜索算法的自我 学习策略。 每个个体通过自我调整进行优化学习。 由于每个学员可能同时学习多门课程（多个决策变 量），在进行“自我”学习时只是对部分科目进行调 整学习，保持优势学科，增强劣势科目。 采用 ３ 种自 我调整策略进行学习： １）向“某一科”较为优秀的同学学习，增强单科 水平。 学习概率为 ＬｏＰ。 ２）自我调整，以概率 ＳＲＰ 进行科目调整，调整 步长为 Ｓｔｅｐ 。 ３）以概率 ＩＬＰ 进行创新学习。 “自我”学习阶段的具体算法如下： Ｆｏｒ ｉ ＝ １ ｔｏ ＮＰ Ｘｎｅｗ ＝ Ｘｉ Ｆｏｒ ｊ ＝ １ ｔｏ ｄ Ｉｆ ｒａｎｄ（）＜ＬｏＰ Ｘｎｅｗ (ｊ) ＝ Ｘａ (ｊ) ，ａ ∈Ｕ{１，２，…，ＮＰ} ； ／ ／ 策略（１） ＥｌｓｅＩｆ ｒａｎｄ（）＜ＳＲＰ Ｘｎｅｗ (ｊ) ＝ Ｘｎｅｗ (ｊ) ±ｒａｎｄ(０，１) × Ｓｔｅｐ(ｊ) ／ ／ 策略（２） Ｅｌｓｅｉｆ ｒａｎｄ（）＜ＩＬＰ Ｘｎｅｗ (ｊ) ＝ ｘ Ｌ (ｊ) ＋ｒａｎｄ × ｘ Ｕ (ｊ) －ｘ Ｌ ( (ｊ) ) ； ／ ／ 策略（３） Ｅｎｄ Ｅｎｄ Ｅｎｄ 其中， Ｓｔｅｐ ＝ ｍｉｎＳｔｅｐ ＋ （ｍａｘＳｔｅｐ － ｍｉｎＳｔｅｐ） １ － ｔ Ｔ æ è ç ö ø ÷ ｍａｘＳｔｅｐ ＝ （ｘ Ｕ － ｘ Ｌ ） ／ ５０ ｍｉｎＳｔｅｐ ＝ （ｘ Ｕ － ｘ Ｌ ） ／ ３ ０００ ｔ 是当且迭代次数， Ｔ 是允许最大迭代次数。 ４ ＭＴＬＢＯ 算法主动悬架ＬＱＲ 控制器优化 ４．１ 车辆主动悬架 ＬＱＲ 控制器模型 本文以单轮车辆模型作为研究对象，如图 ２。 ·６０４· 智 能 系 统 学 报 第 ９ 卷

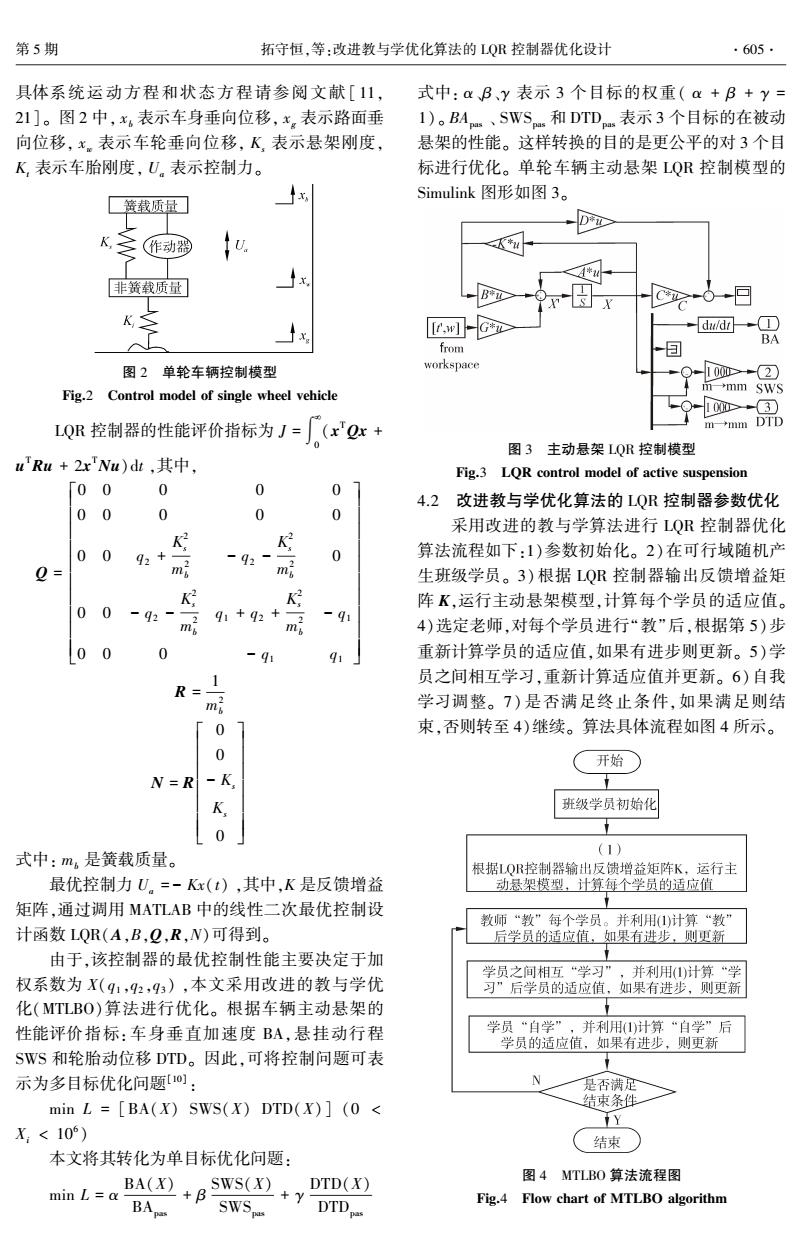
第5期 拓守恒，等：改进教与学优化算法的LQ控制器优化设计 ·605· 具体系统运动方程和状态方程请参阅文献[11， 式中：aB、y表示3个目标的权重(a+B+y= 21]。图2中，x。表示车身垂向位移，x。表示路面垂 1)。BA、SWS和DTD表示3个目标的在被动 向位移，x。表示车轮垂向位移，K,表示悬架刚度， 悬架的性能。这样转换的目的是更公平的对3个目 K表示车胎刚度，U,表示控制力。 标进行优化。单轮车辆主动悬架LQR控制模型的 Simulink图形如图3。 簧载质量 K,作动器 非簧载质量 于x x [tw]-G dw/d+① BA from 图2单轮车辆控制模型 workspace 1000>-2 Fig.2 Control model of single wheel vehicle mmm SWS 10>3 LQR控制器的性能评价指标为J=(xQx+ →nm DTD 图3主动悬架LQR控制模型 u'Ru+2xNu)dt,其中， Fig.3 LOR control model of active suspension 「00 0 0 0 4.2改进教与学优化算法的LQR控制器参数优化 00 0 0 0 采用改进的教与学算法进行LQR控制器优化 K K 0092+ -92- 0 算法流程如下：1)参数初始化。2)在可行域随机产 0= mi m 生班级学员。3)根据LQR控制器输出反馈增益矩 K 阵K,运行主动悬架模型，计算每个学员的适应值。 100 -921 91+92+ -91 mi mi 4)选定老师，对每个学员进行“教”后，根据第5)步 00 0 -9 91 重新计算学员的适应值，如果有进步则更新。5)学 1 员之间相互学习，重新计算适应值并更新。6)自我 R= 学习调整。7)是否满足终止条件，如果满足则结 「0 束，否则转至4)继续。算法具体流程如图4所示。 0 开始 N=R-K K 班级学员初始化 t 0 式中：m。是簧载质量。 (1) 根据1QR控制器输出反馈增益矩阵K,运行主 最优控制力U。=-Kx(t),其中，K是反馈增益 动悬架模型，计算每个学员的适应值 矩阵，通过调用MATLAB中的线性二次最优控制设 教师“教”每个学员。并利用()计算“教” 计函数LQR(A,B,Q,R,N)可得到。 后学员的适应值，如果有进步，则更新 由于，该控制器的最优控制性能主要决定于加 学员之间相互“学习”，并利用计算“学 权系数为X(91,92,93),本文采用改进的教与学优 习”后学员的适应值，如果有进步，则更新 化(MTLBO)算法进行优化。根据车辆主动悬架的 性能评价指标：车身垂直加速度BA,悬挂动行程 学员“自学”，并利用)计算“自学”后 学员的适应值，如果有进步，则更新 SWS和轮胎动位移DTD。因此，可将控制问题可表 示为多目标优化问题]： 是否满足 min L [BA(X)SWS(X)DTD(X)(0 结束条件 Y X:<10) 结束 本文将其转化为单目标优化问题： min L=a BA(X)+B 图4 MTLBO算法流程图 BA sws()+t SWS Fig.4 Flow chart of MTLBO algorithm

具体系统运动方程和状态方程请参阅文献 ［ １１， ２１］。 图 ２ 中， ｘｂ 表示车身垂向位移， ｘｇ 表示路面垂 向位移， ｘｗ 表示车轮垂向位移， Ｋｓ 表示悬架刚度， Ｋｔ 表示车胎刚度， Ｕａ 表示控制力。 图 ２ 单轮车辆控制模型 Ｆｉｇ．２ Ｃｏｎｔｒｏｌ ｍｏｄｅｌ ｏｆ ｓｉｎｇｌｅ ｗｈｅｅｌ ｖｅｈｉｃｌｅ ＬＱＲ 控制器的性能评价指标为 Ｊ ＝ ∫ ¥ ０ （ｘ ＴＱｘ ＋ ｕ ＴＲｕ ＋ ２ｘ ＴＮｕ）ｄｔ ，其中， Ｑ ＝ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ｑ２ ＋ Ｋ ２ ｓ ｍ ２ ｂ － ｑ２ － Ｋ ２ ｓ ｍ ２ ｂ ０ ０ ０ － ｑ２ － Ｋ ２ ｓ ｍ ２ ｂ ｑ１ ＋ ｑ２ ＋ Ｋ ２ ｓ ｍ ２ ｂ － ｑ１ ０ ０ ０ － ｑ１ ｑ１ é ë ê ê ê ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú ú ú ú Ｒ ＝ １ ｍ ２ ｂ Ｎ ＝ Ｒ ０ ０ － Ｋｓ Ｋｓ ０ é ë ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú 式中： ｍｂ 是簧载质量。 最优控制力 Ｕａ ＝ － Ｋｘ（ｔ） ，其中，Ｋ 是反馈增益 矩阵，通过调用 ＭＡＴＬＡＢ 中的线性二次最优控制设 计函数 ＬＱＲ（Ａ，Ｂ，Ｑ，Ｒ，Ｎ）可得到。 由于，该控制器的最优控制性能主要决定于加 权系数为 Ｘ（ｑ１ ，ｑ２ ，ｑ３ ） ，本文采用改进的教与学优 化（ＭＴＬＢＯ）算法进行优化。 根据车辆主动悬架的 性能评价指标：车身垂直加速度 ＢＡ，悬挂动行程 ＳＷＳ 和轮胎动位移 ＤＴＤ。 因此，可将控制问题可表 示为多目标优化问题［１０］ ： ｍｉｎ Ｌ ＝ ［ＢＡ（Ｘ） ＳＷＳ（Ｘ） ＤＴＤ（Ｘ）］ （０ ＜ Ｘｉ ＜ １０ ６ ） 本文将其转化为单目标优化问题： ｍｉｎ Ｌ ＝ α ＢＡ（Ｘ） ＢＡｐａｓ ＋ β ＳＷＳ（Ｘ） ＳＷＳｐａｓ ＋ γ ＤＴＤ（Ｘ） ＤＴＤｐａｓ 式中： α、β、γ 表示 ３ 个目标的权重（ α ＋ β ＋ γ ＝ １）。 ＢＡｐａｓ 、 ＳＷＳｐａｓ 和 ＤＴＤｐａｓ 表示 ３ 个目标的在被动 悬架的性能。 这样转换的目的是更公平的对 ３ 个目 标进行优化。 单轮车辆主动悬架 ＬＱＲ 控制模型的 Ｓｉｍｕｌｉｎｋ 图形如图 ３。 图 ３ 主动悬架 ＬＱＲ 控制模型 Ｆｉｇ．３ ＬＱＲ ｃｏｎｔｒｏｌ ｍｏｄｅｌ ｏｆ ａｃｔｉｖｅ ｓｕｓｐｅｎｓｉｏｎ ４．２ 改进教与学优化算法的 ＬＱＲ 控制器参数优化 采用改进的教与学算法进行 ＬＱＲ 控制器优化 算法流程如下：１）参数初始化。 ２）在可行域随机产 生班级学员。 ３）根据 ＬＱＲ 控制器输出反馈增益矩 阵 Ｋ，运行主动悬架模型，计算每个学员的适应值。 ４）选定老师，对每个学员进行“教”后，根据第 ５）步 重新计算学员的适应值，如果有进步则更新。 ５）学 员之间相互学习，重新计算适应值并更新。 ６）自我 学习调整。 ７） 是否满足终止条件，如果满足则结 束，否则转至 ４）继续。 算法具体流程如图 ４ 所示。 图 ４ ＭＴＬＢＯ 算法流程图 Ｆｉｇ．４ Ｆｌｏｗ ｃｈａｒｔ ｏｆ ＭＴＬＢＯ ａｌｇｏｒｉｔｈｍ 第 ５ 期 拓守恒，等：改进教与学优化算法的 ＬＱＲ 控制器优化设计 ·６０５·

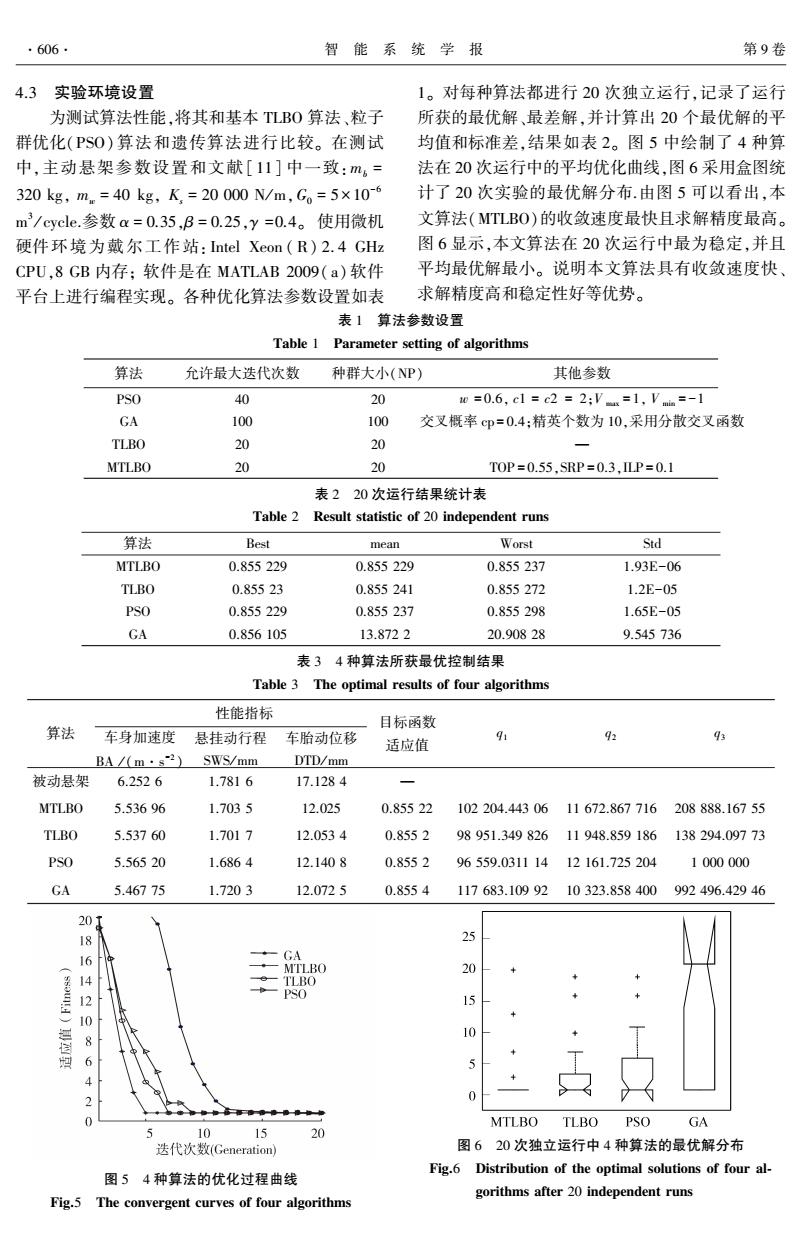
·606 智能系统学报 第9卷 4.3实验环境设置 1。对每种算法都进行20次独立运行，记录了运行 为测试算法性能，将其和基本TLB0算法、粒子 所获的最优解、最差解，并计算出20个最优解的平 群优化(PSO)算法和遗传算法进行比较。在测试 均值和标准差，结果如表2。图5中绘制了4种算 中，主动悬架参数设置和文献[11]中一致：m6= 法在20次运行中的平均优化曲线，图6采用盒图统 320kg,mm=40kg,K,=20000N/m,G。=5×10-6 计了20次实验的最优解分布.由图5可以看出，本 m3/cycle.参数a=0.35,B=0.25,y=0.4。使用微机 文算法(MTLBO)的收敛速度最快且求解精度最高。 硬件环境为戴尔工作站：intel Xeon(R)2.4GHz 图6显示，本文算法在20次运行中最为稳定，并且 CPU,8GB内存：软件是在MATLAB2009(a)软件 平均最优解最小。说明本文算法具有收敛速度快 平台上进行编程实现。各种优化算法参数设置如表 求解精度高和稳定性好等优势。 表1算法参数设置 Table 1 Parameter setting of algorithms 算法 允许最大迭代次数 种群大小(NP) 其他参数 PSO 40 20 w=0.6,c1=c2=2:Vn=1,V=-1 GA 100 100 交叉概率cp=0.4:精英个数为10，采用分散交叉函数 TLBO 20 20 MTLBO 20 T0P=0.55,SRP=0.3,LP=0.1 表220次运行结果统计表 Table 2 Result statistic of 20 independent runs 算法 Best mean Worst Std MTLBO 0.855229 0.855229 0.855237 1.93E-06 TLBO 0.85523 0.855241 0.855272 1.2E-05 PSO 0.855229 0.855237 0.855298 1.65E-05 GA 0.856105 13.8722 20.90828 9.545736 表34种算法所获最优控制结果 Table 3 The optimal results of four algorithms 性能指标 目标函数 算法 车身加速度 悬挂动行程 车胎动位移 91 9 适应值 BAm·s2) SWS/mm DTD/mm 被动悬架 6.2526 1.7816 17.1284 MTLBO 5.53696 1.7035 12.025 0.85522 102204.44306 11672.867716208888.16755 TLBO 5.53760 1.7017 12.0534 0.8552 98951.349826 11948.859186 138294.09773 PSO 5.56520 1.6864 12.1408 0.8552 96559.031114 12161.725204 1000000 GA 5.46775 1.7203 12.0725 0.8554 117683.1099210323.858400992496.42946 20T 伊 25 16 GA MTLBO 20 o- TLBO PSO 15 8 10 6 4 2 0 0 MTLBO TLBO PSO GA 5 10 15 20 迭代次数(Generation) 图620次独立运行中4种算法的最优解分布 Fig.6 Distribution of the optimal solutions of four al- 图54种算法的优化过程曲线 gorithms after 20 independent runs Fig.5 The convergent curves of four algorithms

４．３ 实验环境设置 为测试算法性能，将其和基本 ＴＬＢＯ 算法、粒子 群优化（ＰＳＯ） 算法和遗传算法进行比较。 在测试 中，主动悬架参数设置和文献［ １１］ 中一致：ｍｂ ＝ ３２０ ｋｇ， ｍｗ ＝ ４０ ｋｇ， Ｋｓ ＝ ２０ ０００ Ｎ／ ｍ，Ｇ０ ＝ ５ × １０ －６ ｍ ３ ／ ｃｙｃｌｅ．参数 α ＝ ０．３５，β ＝ ０．２５，γ ＝０．４。 使用微机 硬件环境为戴尔工作站： Ｉｎｔｅｌ Ｘｅｏｎ （ Ｒ） ２． ４ ＧＨｚ ＣＰＵ，８ ＧＢ 内存； 软件是在 ＭＡＴＬＡＢ ２００９（ ａ）软件 平台上进行编程实现。 各种优化算法参数设置如表 １。 对每种算法都进行 ２０ 次独立运行，记录了运行 所获的最优解、最差解，并计算出 ２０ 个最优解的平 均值和标准差，结果如表 ２。 图 ５ 中绘制了 ４ 种算 法在 ２０ 次运行中的平均优化曲线，图 ６ 采用盒图统 计了 ２０ 次实验的最优解分布．由图 ５ 可以看出，本 文算法（ＭＴＬＢＯ）的收敛速度最快且求解精度最高。 图 ６ 显示，本文算法在 ２０ 次运行中最为稳定，并且 平均最优解最小。 说明本文算法具有收敛速度快、 求解精度高和稳定性好等优势。 表 １ 算法参数设置 Ｔａｂｌｅ １ Ｐａｒａｍｅｔｅｒ ｓｅｔｔｉｎｇ ｏｆ ａｌｇｏｒｉｔｈｍｓ 算法 允许最大迭代次数 种群大小（ＮＰ） 其他参数 ＰＳＯ ４０ ２０ ｗ ＝ ０．６， ｃ１ ＝ ｃ２ ＝ ２；Ｖ ｍａｘ ＝ １， Ｖ ｍｉｎ ＝ －１ ＧＡ １００ １００ 交叉概率 ｃｐ ＝ ０．４；精英个数为 １０，采用分散交叉函数 ＴＬＢＯ ２０ ２０ — ＭＴＬＢＯ ２０ ２０ ＴＯＰ ＝ ０．５５，ＳＲＰ ＝ ０．３，ＩＬＰ ＝ ０．１ 表 ２ ２０ 次运行结果统计表 Ｔａｂｌｅ ２ Ｒｅｓｕｌｔ ｓｔａｔｉｓｔｉｃ ｏｆ ２０ ｉｎｄｅｐｅｎｄｅｎｔ ｒｕｎｓ 算法 Ｂｅｓｔ ｍｅａｎ Ｗｏｒｓｔ Ｓｔｄ ＭＴＬＢＯ ０．８５５ ２２９ ０．８５５ ２２９ ０．８５５ ２３７ １．９３Ｅ－０６ ＴＬＢＯ ０．８５５ ２３ ０．８５５ ２４１ ０．８５５ ２７２ １．２Ｅ－０５ ＰＳＯ ０．８５５ ２２９ ０．８５５ ２３７ ０．８５５ ２９８ １．６５Ｅ－０５ ＧＡ ０．８５６ １０５ １３．８７２ ２ ２０．９０８ ２８ ９．５４５ ７３６ 表 ３ ４ 种算法所获最优控制结果 Ｔａｂｌｅ ３ Ｔｈｅ ｏｐｔｉｍａｌ ｒｅｓｕｌｔｓ ｏｆ ｆｏｕｒ ａｌｇｏｒｉｔｈｍｓ 算法 性能指标 车身加速度 ＢＡ ／ （ｍ·ｓ －２ ） 悬挂动行程 ＳＷＳ ／ ｍｍ 车胎动位移 ＤＴＤ／ ｍｍ 目标函数 适应值 ｑ１ ｑ２ ｑ３ 被动悬架 ６．２５２ ６ １．７８１ ６ １７．１２８ ４ — ＭＴＬＢＯ ５．５３６ ９６ １．７０３ ５ １２．０２５ ０．８５５ ２２ １０２ ２０４．４４３ ０６ １１ ６７２．８６７ ７１６ ２０８ ８８８．１６７ ５５ ＴＬＢＯ ５．５３７ ６０ １．７０１ ７ １２．０５３ ４ ０．８５５ ２ ９８ ９５１．３４９ ８２６ １１ ９４８．８５９ １８６ １３８ ２９４．０９７ ７３ ＰＳＯ ５．５６５ ２０ １．６８６ ４ １２．１４０ ８ ０．８５５ ２ ９６ ５５９．０３１１ １４ １２ １６１．７２５ ２０４ １ ０００ ０００ ＧＡ ５．４６７ ７５ １．７２０ ３ １２．０７２ ５ ０．８５５ ４ １１７ ６８３．１０９ ９２ １０ ３２３．８５８ ４００ ９９２ ４９６．４２９ ４６ 图 ５ ４ 种算法的优化过程曲线 Ｆｉｇ．５ Ｔｈｅ ｃｏｎｖｅｒｇｅｎｔ ｃｕｒｖｅｓ ｏｆ ｆｏｕｒ ａｌｇｏｒｉｔｈｍｓ 图 ６ ２０ 次独立运行中 ４ 种算法的最优解分布 Ｆｉｇ．６ Ｄｉｓｔｒｉｂｕｔｉｏｎ ｏｆ ｔｈｅ ｏｐｔｉｍａｌ ｓｏｌｕｔｉｏｎｓ ｏｆ ｆｏｕｒ ａｌ⁃ ｇｏｒｉｔｈｍｓ ａｆｔｅｒ ２０ ｉｎｄｅｐｅｎｄｅｎｔ ｒｕｎｓ ·６０６· 智 能 系 统 学 报 第 ９ 卷