
第9卷第5期 智能系统学报 Vol.9 No.5 2014年10月 CAAI Transactions on Intelligent Systems 0ct.2014 D0:10.3969/j.issn.1673-4785.201304003 动力学解析的四轮全向移动机器人电机解耦控制 王建彬,陈建平2,杨宜民 (1.广东工业大学自动化学院,广东广州510090:2.肇庆学院计算机学院,广东肇庆526061) 摘要:四轮全向移动机器人是一个复杂的非线性、强耦合的机械系统,各轮驱动电机间存在强耦合现象,很难取得 理想的控制效果。针对这一问题,提出一种基于动力学解析的多电机控制系统解耦方法。通过对四轮机器人的动 力学解析推导出四轮转速与其驱动力矩间的状态方程,获得各电机输入输出量之间的耦合关系,在此基础上依据控 制量一致思想设计解耦控制器,解决了传统参考模型解耦方法不能兼顾控制性能和解耦性能的问题,实现了四路电 机的独立控制。仿真结果显示,该方法能够有效地减小控制系统各变量间的相互耦合作用,每路电机均很好地跟踪 了各自的输人,解耦效果好。 关键词:全向移动机器人;动力学解析:解耦控制:电机控制;运动控制 中图分类号:TP273文献标志码:A文章编号:1673-4785(2014)05-0569-08 中文引用格式:王建彬,陈建平,杨宣民.动力学解析的四轮全向移动机器人电机解耦控制[J].智能系统学报,2014,9(5):569- 576. 英文引用格式:WANG Jianbin,CHEN Jianping,YANG Yimin.Motor decoupling control for four-wheel omni-directional mobile ro- bot based on dynamic analysis[J].CAAI Transactions on Intelligent Systems,2014,9(5):569-576. Motor decoupling control for four-wheel omni-directional mobile robot based on dynamic analysis WANG Jianbin',CHEN Jianping',YANG Yimin' (1.School of Automation,Guangdong University of Technology,Guangzhou 510090,China;2.School of Computer Science,Zhaoqing University,Zhaoqing 526061,China) Abstract:An four-wheel omni-directional mobile robot is a complicated nonlinear strong coupling mechanical sys- tem.Since the strong coupling phenomena exist between wheel driven motors,it is difficult to obtain ideal control effect.In order to solve this problem,a decoupling method for multi-motor control based on dynamic analysis is raised in this paper.Through dynamic analysis of the four-wheel robot,the state equation between the four wheels' speed and the driving moment is derived,and the coupling relations between input and output variables of motors are obtained.Furthermore,the decoupling controller is designed according to the consistency idea of controlled vari- ables.Compared with decoupling control of the traditional reference model,the new controller meets both control- ling and decoupling performance,achieving independent control of four motors.Simulation results showed that the method can effectively reduce the coupling interaction between the control variables.Each motor can also track its own input,showing good tracking decoupling effect. Keywords:omni-directional mobile robots;dynamic analysis;decoupling control;motor control;motion control 收稿日期:2013-04-01. 全向移动机器人运动灵活,凭借着不改变位姿 基金项目:广东省自然科学基金资助项目(S2011010004006):广东省教 育部产学研结合资助项目(2012B091100423):肇庆市科技计 就可以向任意方向移动的独特运动优势,已经被广 划资助项目(2010F006):肇庆学院科研启动基金资助项目 (2012BS01). 泛应用于人类的生产、生活实践中山。由于四轮全 通信作者:陈建平.E-mail:jpchen(@zqu.cdu.cn. 向移动机器人是一个结构复杂、强耦合、非线性的机
第 9 卷第 5 期 智 能 系 统 学 报 Vol.9 №.5 2014 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2014 DOI:10.3969 / j.issn.1673⁃4785.201304003 动力学解析的四轮全向移动机器人电机解耦控制 王建彬1 ,陈建平2 ,杨宜民1 (1.广东工业大学 自动化学院,广东 广州 510090; 2.肇庆学院 计算机学院,广东 肇庆 526061) 摘 要:四轮全向移动机器人是一个复杂的非线性、强耦合的机械系统,各轮驱动电机间存在强耦合现象,很难取得 理想的控制效果。 针对这一问题,提出一种基于动力学解析的多电机控制系统解耦方法。 通过对四轮机器人的动 力学解析推导出四轮转速与其驱动力矩间的状态方程,获得各电机输入输出量之间的耦合关系,在此基础上依据控 制量一致思想设计解耦控制器,解决了传统参考模型解耦方法不能兼顾控制性能和解耦性能的问题,实现了四路电 机的独立控制。 仿真结果显示,该方法能够有效地减小控制系统各变量间的相互耦合作用,每路电机均很好地跟踪 了各自的输入,解耦效果好。 关键词:全向移动机器人;动力学解析;解耦控制;电机控制;运动控制 中图分类号: TP273 文献标志码:A 文章编号:1673⁃4785(2014)05⁃0569⁃08 中文引用格式:王建彬,陈建平,杨宜民. 动力学解析的四轮全向移动机器人电机解耦控制[ J]. 智能系统学报, 2014, 9( 5): 569⁃ 576. 英文引用格式:WANG Jianbin,CHEN Jianping,YANG Yimin.Motor decoupling control for four⁃wheel omni⁃directional mobile ro⁃ bot based on dynamic analysis[J]. CAAI Transactions on Intelligent Systems, 2014, 9(5): 569⁃576. Motor decoupling control for four⁃wheel omni⁃directional mobile robot based on dynamic analysis WANG Jianbin 1 , CHEN Jianping 2 , YANG Yimin 1 (1.School of Automation, Guangdong University of Technology, Guangzhou 510090, China; 2. School of Computer Science, Zhaoqing University, Zhaoqing 526061, China) Abstract:An four⁃wheel omni⁃directional mobile robot is a complicated nonlinear strong coupling mechanical sys⁃ tem. Since the strong coupling phenomena exist between wheel driven motors, it is difficult to obtain ideal control effect. In order to solve this problem, a decoupling method for multi⁃motor control based on dynamic analysis is raised in this paper. Through dynamic analysis of the four⁃wheel robot, the state equation between the four wheels’ speed and the driving moment is derived, and the coupling relations between input and output variables of motors are obtained. Furthermore, the decoupling controller is designed according to the consistency idea of controlled vari⁃ ables. Compared with decoupling control of the traditional reference model, the new controller meets both control⁃ ling and decoupling performance, achieving independent control of four motors. Simulation results showed that the method can effectively reduce the coupling interaction between the control variables. Each motor can also track its own input, showing good tracking decoupling effect. Keywords:omni⁃directional mobile robots; dynamic analysis; decoupling control; motor control; motion control 收稿日期:2013⁃04⁃01. 基金项目:广东省自然科学基金资助项目( S2011010004006);广东省教 育部产学研结合资助项目(2012B091100423);肇庆市科技计 划资助项目(2010F006);肇庆学院科研启动基金资助项目 (2012BS01). 通信作者:陈建平. E⁃mail:jpchen@ zqu.edu.cn. 全向移动机器人运动灵活,凭借着不改变位姿 就可以向任意方向移动的独特运动优势,已经被广 泛应用于人类的生产、生活实践中[1] 。 由于四轮全 向移动机器人是一个结构复杂、强耦合、非线性的机

·570· 智能系统学报 第9卷 械系统,各个轮子驱动电机间存在耦合现象,对其中 1各电机输入输出量间的耦合关系 任一电机的控制都会引起其他3个电机状态的变 化,因此对各个电机进行解耦控制是十分迫切和必 1.1四轮全向移动机器人的动力学模型 要的[],目前国内外关于四轮全向移动机器人的电 目前,在全向移动机器人轮系分布系统设计中, 机解耦控制方面的研究报告仍比较少见3)]。 主要有三轮均衡分布及四轮均衡分布2种类型。由 四轮全向移动机器人电机控制系统是一个典型 于本实验室所用比赛足球机器人的射门机构的增 的MIMO系统,对于多变量系统的解耦问题,通常均 加,导致4个全向轮不是对称分布,而是如图1所 采用参考模型控制的方法进行,而关于这类解耦方 示114,前两轮夹角为120°,后两轮为90°。 法的研究目前已经有很多6。文献[7]对具有4个 操作轮的小车控制系统,通过测量反馈和动力学模 型,提出一种基于状态反馈的参考模型解耦控制方 法:文献[8]针对具有参数跳变的多变量系统,提出 一种基于分层递阶结构的多模型自适应前馈解耦控 制器;R.Suzuki等把模型参考与内模原理结合,构 造了一种基于内模的参考模型解耦控制方法[):文 献[10]通过将滑模变结构理论与模型参考方法融 合,设计了一种滑模模型参考控制方法;文献[11] 把神经网络理论与模型参考方法结合,提出基于多 标量模型的感应电机神经网络逆控制结构,实现感 图1四轮全向机器人的结构 应电机系统的自适应解耦线性化:文献[12]将模糊 Fig.1 Structure of the robot 控制引入感应电动机解耦变结构系统可以有效地抑 设机器人任一时刻质心的位姿为[xy)]T, 制抖振,从而提出了采用模糊控制的感应电动机模 P1、P2、P3、中:为4个车轮的角位移,取机器人广义 型参考解耦控制系统。这些方法都是通过设计参考 位姿q=[xy0p1P2pp4]T,各轮转速为y= 模型对控制器的参数进行调整,控制和解耦功能均 [P192中3中4]「,则有机器人运动学方程: 由同一个控制器实现,难以同时兼顾控制与解耦的 q=S(q)v (1) 性能,而且设计原理和方法都较复杂,因此在工程实 式中:S(q)为转换矩阵,其表达式为 践中,寻求简单易行的有效解耦方法是目前普遍关 S(q)= 注的问题。文献[13]提出了一种基于控制量一致 [-sin(0+δ,)sin(0-8,)sin(0+d)-sin(0-6,)1 思想的参考模型解耦方法,通过设计合理的解耦控 rc0s(0+81) -c0s(0-6)-c0s(0+8)Tc0s(0-64) 制器,实现了耦合关系已知的双通道耦合模型的动 r/l r/l r/l r/l 静态解耦。然而却没有考虑更加复杂的多通道耦合 0 0 0 系统及耦合关系不确定或未知的情况。 0 1 0 0 为此,提出一种基于动力学解析的四轮驱动机 0 0 1 0 器人电机解耦控制方法。首先,通过动力学解析获 0 0 得各轮驱动电机输入输出量之间的耦合关系式,然 (2) 后基于控制量一致思想,设计了四轮机器人电机控 式中,0为机器人的运动方向,1为机器人质心到各 制系统的解耦控制器,实现了控制功能与解耦功能 轮子的距离,r为轮子的半径。 的分离,且控制器结构简单,便于实际应用。仿真结 取机器人的质量为m,绕质心的转动惯量为J, 果表明,针对不同的输入情况,四路电机都能够很好 机器人4个轮子受到的阻力分别为F1、F2、F,、F4, 地跟踪各自的控制目标,实现了控制系统的动静态 各个轮子的输出力矩为T:、T2、T3、T4,各个轮子的 解耦。 转动惯量分别为J1、J2、J3、J4,由牛顿第二定律可
械系统,各个轮子驱动电机间存在耦合现象,对其中 任一电机的控制都会引起其他 3 个电机状态的变 化,因此对各个电机进行解耦控制是十分迫切和必 要的[2] ,目前国内外关于四轮全向移动机器人的电 机解耦控制方面的研究报告仍比较少见[3⁃5] 。 四轮全向移动机器人电机控制系统是一个典型 的 MIMO 系统,对于多变量系统的解耦问题,通常均 采用参考模型控制的方法进行,而关于这类解耦方 法的研究目前已经有很多[6] 。 文献[7]对具有 4 个 操作轮的小车控制系统,通过测量反馈和动力学模 型,提出一种基于状态反馈的参考模型解耦控制方 法;文献[8]针对具有参数跳变的多变量系统,提出 一种基于分层递阶结构的多模型自适应前馈解耦控 制器; R. Suzuki 等把模型参考与内模原理结合, 构 造了一种基于内模的参考模型解耦控制方法[9] ;文 献[10]通过将滑模变结构理论与模型参考方法融 合, 设计了一种滑模模型参考控制方法;文献[11] 把神经网络理论与模型参考方法结合,提出基于多 标量模型的感应电机神经网络逆控制结构,实现感 应电机系统的自适应解耦线性化;文献[12] 将模糊 控制引入感应电动机解耦变结构系统可以有效地抑 制抖振,从而提出了采用模糊控制的感应电动机模 型参考解耦控制系统。 这些方法都是通过设计参考 模型对控制器的参数进行调整,控制和解耦功能均 由同一个控制器实现,难以同时兼顾控制与解耦的 性能,而且设计原理和方法都较复杂,因此在工程实 践中,寻求简单易行的有效解耦方法是目前普遍关 注的问题。 文献[13]提出了一种基于控制量一致 思想的参考模型解耦方法,通过设计合理的解耦控 制器,实现了耦合关系已知的双通道耦合模型的动 静态解耦。 然而却没有考虑更加复杂的多通道耦合 系统及耦合关系不确定或未知的情况。 为此,提出一种基于动力学解析的四轮驱动机 器人电机解耦控制方法。 首先,通过动力学解析获 得各轮驱动电机输入输出量之间的耦合关系式,然 后基于控制量一致思想,设计了四轮机器人电机控 制系统的解耦控制器,实现了控制功能与解耦功能 的分离,且控制器结构简单,便于实际应用。 仿真结 果表明,针对不同的输入情况,四路电机都能够很好 地跟踪各自的控制目标,实现了控制系统的动静态 解耦。 1 各电机输入输出量间的耦合关系 1.1 四轮全向移动机器人的动力学模型 目前,在全向移动机器人轮系分布系统设计中, 主要有三轮均衡分布及四轮均衡分布 2 种类型。 由 于本实验室所用比赛足球机器人的射门机构的增 加,导致 4 个全向轮不是对称分布,而是如图 1 所 示[14] ,前两轮夹角为 120 ° ,后两轮为 90 ° 。 图 1 四轮全向机器人的结构 Fig.1 Structure of the robot 设机器人任一时刻质心的位姿为 [ x y θ)] T , φ1 、 φ2 、 φ3 、 φ4 为 4 个车轮的角位移,取机器人广义 位姿 q = [x y θ φ1 φ2 φ3 φ4 ] T , 各 轮 转 速 为 v = [φ · 1 φ · 2 φ · 3 φ · 4 ] T ,则有机器人运动学方程: q · = S(q)v (1) 式中: S(q) 为转换矩阵,其表达式为 S(q) = -rsin(θ +δ1) rsin(θ -δ2) rsin(θ +δ3) -rsin(θ -δ4) rcos(θ +δ1) -rcos(θ -δ2) -rcos(θ +δ3) rcos(θ -δ4) r/ l r/ l r/ l r/ l 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 é ë ê ê ê ê ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú ú ú ú ú (2) 式中, θ 为机器人的运动方向, l 为机器人质心到各 轮子的距离, r 为轮子的半径。 取机器人的质量为 m ,绕质心的转动惯量为 J, 机器人 4 个轮子受到的阻力分别为 F1 、 F2 、 F3 、 F4 , 各个轮子的输出力矩为 T1 、 T2 、 T3 、 T4 ,各个轮子的 转动惯量分别为 J1 、 J2 、 J3 、 J4 ,由牛顿第二定律可 ·570· 智 能 系 统 学 报 第 9 卷

第5期 王建彬,等:动力学解析的四轮全向移动机器人电机解耦控制 ·571- 得动力学方程如下: 其中矩阵Z中各元素的表达式为 mx+F1sin(0+61)-F2sin(0-82) 2 ,C0s282 -F3sin(0+83)+F4sin(8-84)=0 n3* 1=J1+ rr m -+p2(m n216c0s28 my-F1cos(0+81)+F2cos(0-82)+ 2 m +p2(-m+- F3cos(0+63)-F4cos(0-64)=0 16cos5,sin 2 J0-F l-F2l2 F3ls-Fl=0 (3) m -16c0s5.sin.m J+Fr=T -2 J202+F2r=T2 r m .c0s28, J303 F3r =T3 Ja+Fr=T 矩阵W中各元素的表达式为 进一步整理为拉格朗日标准形式有 Cw Mg=Ex-H'(q)入 (4 01=Cm+ n 式中: H(q)= w=pmr2 4n2sinδ2 1) cos(8+8)sin(9+8,)-1T00 0 ws pmr2 1 n(、 -+ -)8 cos(0-82)sin(0-62)-l0r00 sinδ,cos0, cos(9+83)sin(9+83)-l00r0 0,s、Pr2 18 cos(0-84)sin(0-6a)-l000r M=diag(m,m,J小h)1-0r 「00 限于篇幅,其他系数未列出,其中J(i=1,2,3, 为单位对角方阵,A=[F,F,F,F],T= 4)为折算到各个驱动电机的转动惯量,cm和c.分 [T,T2T3T4]T。 别为各个驱动电机和对应轮子的阻尼系数,n为电 式(4)两端乘以S(q),且由式(1)、(3)可得图 1 1所示的移动机器人动力学模型: 机齿轮减速比,p=2(c0sd,+sin6,) T=S"(q)Mq 令w=v,则式(6)进一步化简得到机器人四轮 (5) 速度与其驱动力矩间的状态方程: 1.2各电机输入输出量间耦合关系的推导 对式(1)两端求导,并将式(5)代入可得 ω=A0+Br (9) i=-(s(q)Ms(q))-Is"(q)MS(q)v+(6) 式中:状态矩阵A和B为4×4的方阵,且 (S(q)MS(q))-17 A=Z-W.B=Z- (10) 取4×4的方阵Z和M分别为 由式(8)和(10)可知,系统状态矩阵A是关于各轮 31222324 转速的非线性矩阵,因此本文在实际计算中,用其在 22252623 Z=S(q)MS(q)= (7) 平衡点附近的近似线性化矩阵A来代替,从而有 23262522 @=A@+BT (11) 24232231」 由式(11)可知,四轮驱动机器人的电机控制系统是 1011021030d 一个4输入4输出的耦合系统,需要进行解耦以达 -10210110503 W=S(g)MS(g)= (8) 到对4个电机的独立控制。假设系统的输出方程为 -10310510102 Y=Cw,则由线性系统理论知识可得系统的传递函 数矩阵为
得动力学方程如下: mx ¨ + F1 sin(θ + δ1 ) - F2 sin(θ - δ2 ) - F3 sin(θ + δ3 ) + F4 sin(θ - δ4 ) = 0 my ¨ - F1 cos(θ + δ1 ) + F2 cos(θ - δ2 ) + F3 cos(θ + δ3 ) - F4 cos(θ - δ4 ) = 0 Jθ ¨ - F1 l 1 - F2 l 2 - F3 l 3 - F4 l 4 = 0 J1φ ¨ 1 + F1 r = T1 J2φ ¨ 2 + F2 r = T2 J3φ ¨ 3 + F3 r = T3 J4φ ¨ 4 + F4 r = T4 (3) 进一步整理为拉格朗日标准形式有 Mq ¨ = Eτ - H T (q)λ (4) 式中: H(q) = cos(θ + δ1 ) sin(θ + δ1 ) - l r 0 0 0 cos(θ - δ2 ) sin(θ - δ2 ) - l 0 r 0 0 cos(θ + δ3 ) sin(θ + δ3 ) - l 0 0 r 0 cos(θ - δ4 ) sin(θ - δ4 ) - l 0 0 0 r é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú M = diag(m,m,J,J1 ,J2 ,J3 ,J4 ),I = 0 0 0 I′ 4×4 é ë ê ê ù û ú ú I' 为 单 位 对 角 方 阵, λ = [F1 F2 F3 F4 ] T , τ = [T1 T2 T3 T4 ] T 。 式(4)两端乘以 S T (q) ,且由式(1)、(3)可得图 1 所示的移动机器人动力学模型: τ = S T (q)Mq ¨ (5) 1.2 各电机输入输出量间耦合关系的推导 对式(1)两端求导,并将式(5)代入可得 v · = - (S T (q)MS(q)) - 1S T (q)MS · (q)v + (S T (q)MS(q)) - 1τ (6) 取 4 × 4 的方阵 Z 和 M 分别为 Z = S T (q)MS(q) = z1 z2 z3 z4 z2 z5 z6 z3 z3 z6 z5 z2 z4 z3 z2 z1 é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú (7) W = S T (q)MS · (q) = w1 w2 w3 w4 - w2 w1 w5 w3 - w3 w5 w1 w2 - w4 - w3 - w2 w1 é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú (8) 其中矩阵 Z 中各元素的表达式为 z1 = J ^ 1 + J1 n 2 + r 2 n 2 [ m 16 cos 2 δ 1 + ρ 2 (m + cos 2 δ 2 L 2 J)] z2 = r 2 n 2 [ m 16cosδ 1 sinδ 2 + ρ 2 ( - m + sinδ 1 cosδ 2 L 2 J)] z3 = r 2 n 2 [ - m 16cosδ 1 sinδ 2 + ρ 2 ( - m + sinδ 1 cosδ 2 L 2 J)] z4 = r 2 n 2 [ - m 16 cos 2 δ 1 + ρ 2 (m + cos 2 δ 2 L 2 J)] … 矩阵 W 中各元素的表达式为 w1 = cm + cw n 2 w2 = ρmr 2 4n 2 ( 1 sinδ 2 + 1 cosδ 1 )θ · w3 = ρmr 2 4n 2 ( - 1 sinδ 2 + 1 cosδ 1 )θ · w4 = - ρmr 2 2n 2 · 1 cosδ 1 θ · … 限于篇幅,其他系数未列出,其中 J ^ i ( i = 1,2,3, 4 )为折算到各个驱动电机的转动惯量, cm 和 cw 分 别为各个驱动电机和对应轮子的阻尼系数, n 为电 机齿轮减速比, ρ = 1 2(cos δ 1 + sin δ 2 ) 。 令 ω = v ,则式(6)进一步化简得到机器人四轮 速度与其驱动力矩间的状态方程: ω · = A ~ ω + Bτ (9) 式中:状态矩阵 A ~ 和 B 为 4 × 4 的方阵,且 A ~ = Z -1W,B = Z -1 (10) 由式(8)和(10)可知,系统状态矩阵 A ~ 是关于各轮 转速的非线性矩阵,因此本文在实际计算中,用其在 平衡点附近的近似线性化矩阵 A 来代替,从而有 ω · = Aω + Bτ (11) 由式(11)可知,四轮驱动机器人的电机控制系统是 一个 4 输入 4 输出的耦合系统,需要进行解耦以达 到对 4 个电机的独立控制。 假设系统的输出方程为 Y = Cω ,则由线性系统理论知识可得系统的传递函 数矩阵为 第 5 期 王建彬,等:动力学解析的四轮全向移动机器人电机解耦控制 ·571·
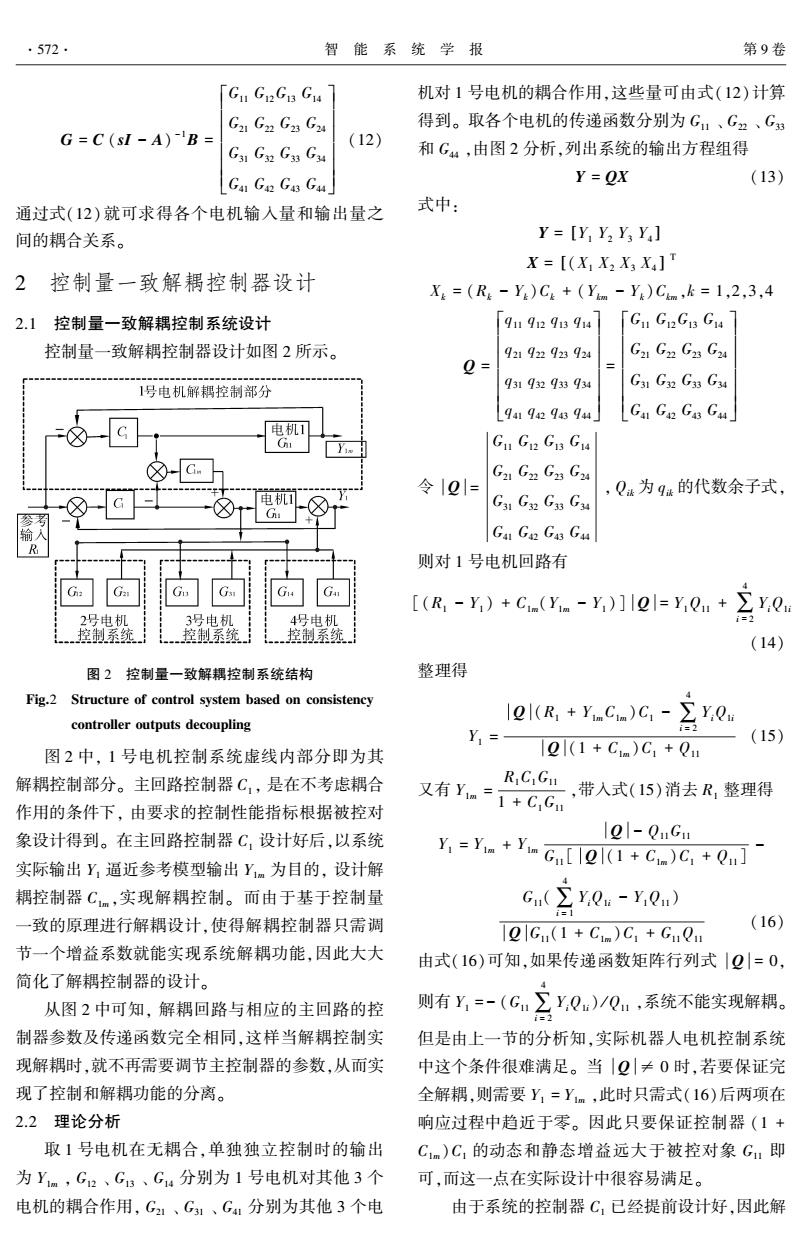
.572. 智能系统学报 第9卷 「G1GG3G4 机对1号电机的耦合作用,这些量可由式(12)计算 Ga Gn Ga Gu 得到。取各个电机的传递函数分别为G、G2、G知 G=C(sI-A)B= (12) Ga Gn Ga Gu 和G44,由图2分析,列出系统的输出方程组得 G41GG43G44 Y=OX (13) 通过式(12)就可求得各个电机输入量和输出量之 式中: 间的耦合关系。 Y=[Y,Y,Y3 Y] X=[(X X2 X3 X]T 2控制量一致解耦控制器设计 X=(R-Y)C5+(Ym-Y)Cm,k=1,2,3,4 2.1控制量一致解耦控制系统设计 911912913914 [Gu GRGB Gu 控制量一致解耦控制器设计如图2所示。 921922923924 G21G2G23G24 0= 1号电机解耦控制部分 931932933934 G31G32G3G34 L94194294394J Ga GR Ga Gu 电机1 Gu GR2 GB Gu G2 G22 G3 G24 令I01= ,Q为9k的代数余子式, 电机1 Ga Gx Ga Gu n 输入 G41G42G43G44 则对1号电机回路有 G [(R -Y)+Ci(Yim -Y,)]l21=Yn+ 2号电机 3号电机 4号电机 立Q 控制系统 控拟系统 控制系统。 (14) 图2控制量一致解耦控制系统结构 整理得 Fig.2 Structure of control system based on consistency controller outputs decoupling |Ql(R,+yCa)C-∑yQm Y1= (15) 图2中,1号电机控制系统虚线内部分即为其 1(1+Cim)C+u 解耦控制部分。主回路控制器C,是在不考虑耦合 RC,G,带入式(15)消去R,整理得 作用的条件下,由要求的控制性能指标根据被控对 又有Ym=1+C,Gm 象设计得到。在主回路控制器C,设计好后,以系统 121-QnGu 实际输出Y,逼近参考模型输出Y1m为目的,设计解 Y=Y+Y Cu[el(1+C)C+u] 耦控制器Cm,实现解耦控制。而由于基于控制量 G(∑y,Q-y,Q) 一致的原理进行解耦设计,使得解耦控制器只需调 (16) QGu(1+Cim)C:+GuQ 节一个增益系数就能实现系统解耦功能,因此大大 由式(16)可知,如果传递函数矩阵行列式|Q=0, 简化了解耦控制器的设计。 从图2中可知,解耦回路与相应的主回路的控 则有y-(Gn三yQ)/0u,系统不能实现解耦。 制器参数及传递函数完全相同,这样当解耦控制实 但是由上一节的分析知,实际机器人电机控制系统 现解耦时,就不再需要调节主控制器的参数,从而实 中这个条件很难满足。当|Q|≠0时,若要保证完 现了控制和解耦功能的分离。 全解耦,则需要Y=Ym,此时只需式(16)后两项在 2.2理论分析 响应过程中趋近于零。因此只要保证控制器(1+ 取1号电机在无耦合,单独独立控制时的输出 C1m)C,的动态和静态增益远大于被控对象G,即 为Ym,G2、G:、G4分别为1号电机对其他3个 可,而这一点在实际设计中很容易满足。 电机的耦合作用,G2:、G31、G41分别为其他3个电 由于系统的控制器C,已经提前设计好,因此解
G = C (sI - A) -1B = G11 G12G13 G14 G21 G22 G23 G24 G31 G32 G33 G34 G41 G42 G43 G44 é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú (12) 通过式(12)就可求得各个电机输入量和输出量之 间的耦合关系。 2 控制量一致解耦控制器设计 2.1 控制量一致解耦控制系统设计 控制量一致解耦控制器设计如图 2 所示。 图 2 控制量一致解耦控制系统结构 Fig.2 Structure of control system based on consistency controller outputs decoupling 图 2 中, 1 号电机控制系统虚线内部分即为其 解耦控制部分。 主回路控制器 C1 , 是在不考虑耦合 作用的条件下, 由要求的控制性能指标根据被控对 象设计得到。 在主回路控制器 C1 设计好后,以系统 实际输出 Y1 逼近参考模型输出 Y1m 为目的, 设计解 耦控制器 C1m ,实现解耦控制。 而由于基于控制量 一致的原理进行解耦设计,使得解耦控制器只需调 节一个增益系数就能实现系统解耦功能,因此大大 简化了解耦控制器的设计。 从图 2 中可知, 解耦回路与相应的主回路的控 制器参数及传递函数完全相同,这样当解耦控制实 现解耦时,就不再需要调节主控制器的参数,从而实 现了控制和解耦功能的分离。 2.2 理论分析 取 1 号电机在无耦合,单独独立控制时的输出 为 Y1m , G12 、 G13 、 G14 分别为 1 号电机对其他 3 个 电机的耦合作用, G21 、 G31 、 G41 分别为其他 3 个电 机对 1 号电机的耦合作用,这些量可由式(12)计算 得到。 取各个电机的传递函数分别为 G11 、 G22 、 G33 和 G44 ,由图 2 分析,列出系统的输出方程组得 Y = QX (13) 式中: Y = Y1 Y2 Y3 Y4 [ ] X = (X1 X2 X3 X4 [ ] T Xk = (Rk - Yk)Ck + (Ykm - Yk)Ckm ,k = 1,2,3,4 Q = q11 q12 q13 q14 q21 q22 q23 q24 q31 q32 q33 q34 q41 q42 q43 q44 é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú = G11 G12G13 G14 G21 G22 G23 G24 G31 G32 G33 G34 G41 G42 G43 G44 é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú 令 Q = G11 G12 G13 G14 G21 G22 G23 G24 G31 G32 G33 G34 G41 G42 G43 G44 , Qik 为 qik 的代数余子式, 则对 1 号电机回路有 [(R1 - Y1 ) + C1m(Y1m - Y1 )] Q = Y1Q11 + ∑ 4 i = 2 YiQ1i (14) 整理得 Y1 = Q (R1 + Y1m C1m )C1 - ∑ 4 i = 2 YiQ1i Q (1 + C1m )C1 + Q11 (15) 又有 Y1m = R1C1G11 1 + C1G11 ,带入式(15)消去 R1 整理得 Y1 = Y1m + Y1m Q - Q11G11 G11 [ Q (1 + C1m )C1 + Q11 ] - G11(∑ 4 i = 1 YiQ1i - Y1Q11 ) Q G11(1 + C1m )C1 + G11Q11 (16) 由式(16)可知,如果传递函数矩阵行列式 Q = 0, 则有 Y1 = - (G11∑ 4 i = 2 YiQ1i) / Q11 ,系统不能实现解耦。 但是由上一节的分析知,实际机器人电机控制系统 中这个条件很难满足。 当 Q ≠ 0 时,若要保证完 全解耦,则需要 Y1 = Y1m ,此时只需式(16)后两项在 响应过程中趋近于零。 因此只要保证控制器 (1 + C1m )C1 的动态和静态增益远大于被控对象 G11 即 可,而这一点在实际设计中很容易满足。 由于系统的控制器 C1 已经提前设计好,因此解 ·572· 智 能 系 统 学 报 第 9 卷
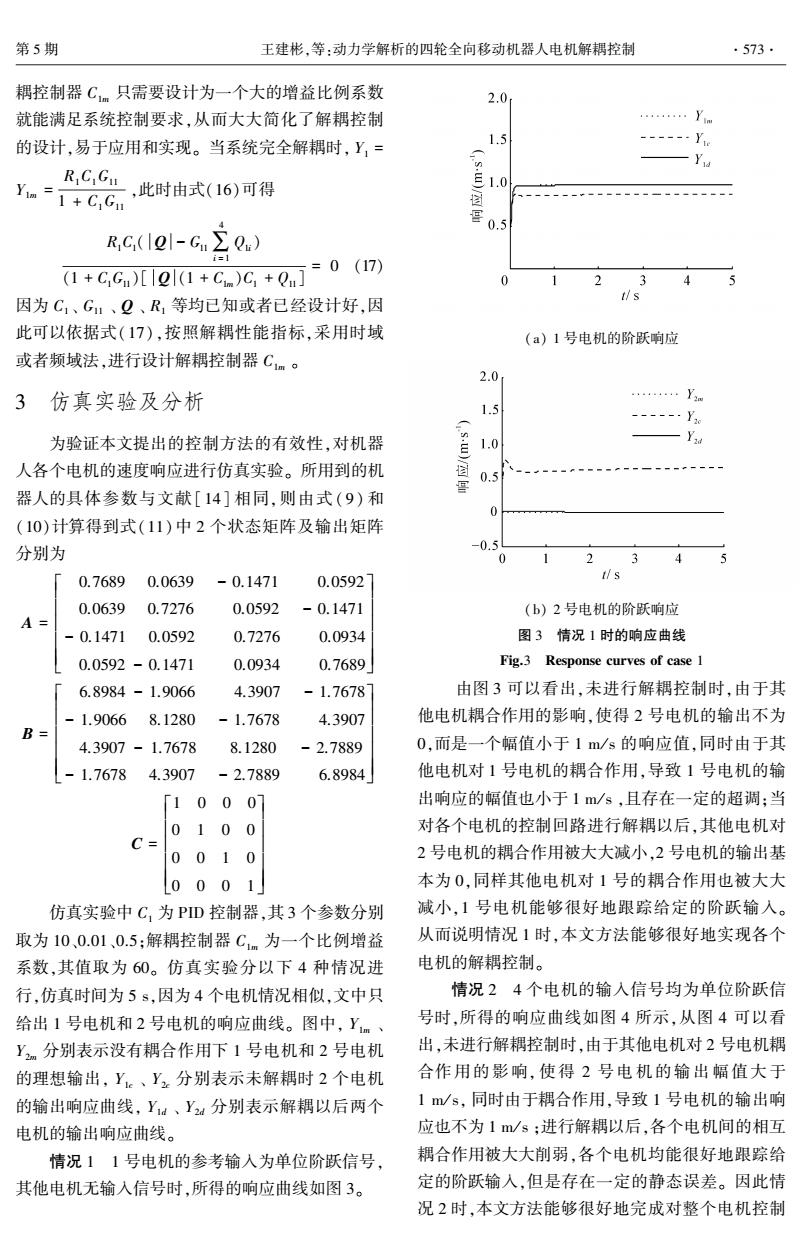
第5期 王建彬,等:动力学解析的四轮全向移动机器人电机解耦控制 ·573· 耦控制器Cm只需要设计为一个大的增益比例系数 2.0 就能满足系统控制要求,从而大大简化了解耦控制 …Yn 的设计,易于应用和实现。当系统完全解耦时,Y,= 1.5 ---…Ye R,C,G,此时由式(16)可得 1+C,G11 e05 R,C(lgl-G.∑Q.) (+GG)l(c+]0 ( i=1 2 3 4 5 t/s 因为C、G!、Q、R,等均已知或者已经设计好,因 此可以依据式(17),按照解耦性能指标,采用时域 (a)1号电机的阶跃响应 或者频域法,进行设计解耦控制器C1m。 2.0 3仿真实验及分析 小Yn 1.5 ----Y 为验证本文提出的控制方法的有效性,对机器 1.0 人各个电机的速度响应进行仿真实验。所用到的机 0.5 督 器人的具体参数与文献[14]相同,则由式(9)和 0 (10)计算得到式(11)中2个状态矩阵及输出矩阵 分别为 -0.5 0 23 4 5 0.7689 0.0639 -0.1471 0.0592 ∥s 0.0639 0.7276 0.0592 -0.1471 (b)2号电机的阶跃响应 A= -0.1471 0.0592 0.7276 0.0934 图3情况1时的响应曲线 0.0592-0.1471 0.0934 0.7689」 Fig.3 Response curves of case 1 6.8984-1.9066 4.3907 -1.7678 由图3可以看出,未进行解耦控制时,由于其 -1.9066 8.1280 -1.7678 4.3907 他电机耦合作用的影响,使得2号电机的输出不为 B= 4.3907-1.7678 8.1280 -2.7889 0,而是一个幅值小于1m/s的响应值,同时由于其 -1.7678 4.3907 -2.7889 6.8984 他电机对1号电机的耦合作用,导致1号电机的输 「10007 出响应的幅值也小于1m/s,且存在一定的超调:当 01 0 0 对各个电机的控制回路进行解耦以后,其他电机对 C= 001 0 2号电机的耦合作用被大大减小,2号电机的输出基 L000 1 本为0,同样其他电机对1号的耦合作用也被大大 仿真实验中C,为PD控制器,其3个参数分别 减小,1号电机能够很好地跟踪给定的阶跃输入。 取为100.01、0.5;解耦控制器Cm为一个比例增益 从而说明情况1时,本文方法能够很好地实现各个 系数,其值取为60。仿真实验分以下4种情况进 电机的解耦控制。 行,仿真时间为5s,因为4个电机情况相似,文中只 情况24个电机的输入信号均为单位阶跃信 给出1号电机和2号电机的响应曲线。图中,Ym、 号时,所得的响应曲线如图4所示,从图4可以看 Y2m分别表示没有耦合作用下1号电机和2号电机 出,未进行解耦控制时,由于其他电机对2号电机耦 的理想输出,Yk、Y,分别表示未解耦时2个电机 合作用的影响,使得2号电机的输出幅值大于 的输出响应曲线,Y、Y2a分别表示解耦以后两个 1/s,同时由于耦合作用,导致1号电机的输出响 电机的输出响应曲线。 应也不为1m/s;进行解耦以后,各个电机间的相互 情况11号电机的参考输入为单位阶跃信号, 耦合作用被大大削弱,各个电机均能很好地跟踪给 其他电机无输入信号时,所得的响应曲线如图3。 定的阶跃输入,但是存在一定的静态误差。因此情 况2时,本文方法能够很好地完成对整个电机控制
耦控制器 C1m 只需要设计为一个大的增益比例系数 就能满足系统控制要求,从而大大简化了解耦控制 的设计,易于应用和实现。 当系统完全解耦时, Y1 = Y1m = R1C1G11 1 + C1G11 ,此时由式(16)可得 R1C1( Q - G11∑ 4 i = 1 Q1i) (1 + C1G11)[ Q (1 + C1m)C1 + Q11] = 0 (17) 因为 C1 、 G11 、 Q 、 R1 等均已知或者已经设计好,因 此可以依据式(17),按照解耦性能指标,采用时域 或者频域法,进行设计解耦控制器 C1m 。 3 仿真实验及分析 为验证本文提出的控制方法的有效性,对机器 人各个电机的速度响应进行仿真实验。 所用到的机 器人的具体参数与文献[ 14] 相同,则由式( 9) 和 (10)计算得到式(11)中 2 个状态矩阵及输出矩阵 分别为 A = 0.7689 0.0639 - 0.1471 0.0592 0.0639 0.7276 0.0592 - 0.1471 - 0.1471 0.0592 0.7276 0.0934 0.0592 - 0.1471 0.0934 0.7689 é ë ê ê ê ê ê ù û ú ú ú ú ú B = 6.8984 - 1.9066 4.3907 - 1.7678 - 1.9066 8.1280 - 1.7678 4.3907 4.3907 - 1.7678 8.1280 - 2.7889 - 1.7678 4.3907 - 2.7889 6.8984 é ë ê ê ê ê ê ù û ú ú ú ú ú C = 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 é ë ê ê ê ê ê ù û ú ú ú ú ú 仿真实验中 C1 为 PID 控制器,其 3 个参数分别 取为 10、0.01、0.5;解耦控制器 C1m 为一个比例增益 系数,其值取为 60。 仿真实验分以下 4 种情况进 行,仿真时间为 5 s,因为 4 个电机情况相似,文中只 给出 1 号电机和 2 号电机的响应曲线。 图中, Y1m 、 Y2m 分别表示没有耦合作用下 1 号电机和 2 号电机 的理想输出, Y1c 、 Y2c 分别表示未解耦时 2 个电机 的输出响应曲线, Y1d 、 Y2d 分别表示解耦以后两个 电机的输出响应曲线。 情况 1 1 号电机的参考输入为单位阶跃信号, 其他电机无输入信号时,所得的响应曲线如图 3。 (a) 1 号电机的阶跃响应 (b) 2 号电机的阶跃响应 图 3 情况 1 时的响应曲线 Fig.3 Response curves of case 1 由图 3 可以看出,未进行解耦控制时,由于其 他电机耦合作用的影响,使得 2 号电机的输出不为 0,而是一个幅值小于 1 m / s 的响应值,同时由于其 他电机对 1 号电机的耦合作用,导致 1 号电机的输 出响应的幅值也小于 1 m / s ,且存在一定的超调;当 对各个电机的控制回路进行解耦以后,其他电机对 2 号电机的耦合作用被大大减小,2 号电机的输出基 本为 0,同样其他电机对 1 号的耦合作用也被大大 减小,1 号电机能够很好地跟踪给定的阶跃输入。 从而说明情况 1 时,本文方法能够很好地实现各个 电机的解耦控制。 情况 2 4 个电机的输入信号均为单位阶跃信 号时,所得的响应曲线如图 4 所示,从图 4 可以看 出,未进行解耦控制时,由于其他电机对 2 号电机耦 合作用的影响, 使得 2 号电机的输出幅值大于 1 m / s, 同时由于耦合作用,导致 1 号电机的输出响 应也不为 1 m / s ;进行解耦以后,各个电机间的相互 耦合作用被大大削弱,各个电机均能很好地跟踪给 定的阶跃输入,但是存在一定的静态误差。 因此情 况 2 时,本文方法能够很好地完成对整个电机控制 第 5 期 王建彬,等:动力学解析的四轮全向移动机器人电机解耦控制 ·573·