
2 2 1 例:求3阶方阵A= 31 5 的逆矩阵。 23 3 解:|A|=1,M=-7,M2=-6,M3=3, M21=4,M2=3,M3=-2, M31=9,M32=7,M3=-4, 则 A A A31 An As Aus A23 A33 M -M M -7 -4 -MR Mn -M2 三 3 -7 M3 -M2 M3 3 2 -4

(1 23 例1 A=221,求A1. 设 3 43 12 310 0 解(AE)= 221 0 10 343 0 0 1 22 2 3 0 -2 5-210 +2 3-3新0-2 -6-301g-2

问题3: 为什么通常不直接用求 逆矩阵的办法来解线性 方程组?
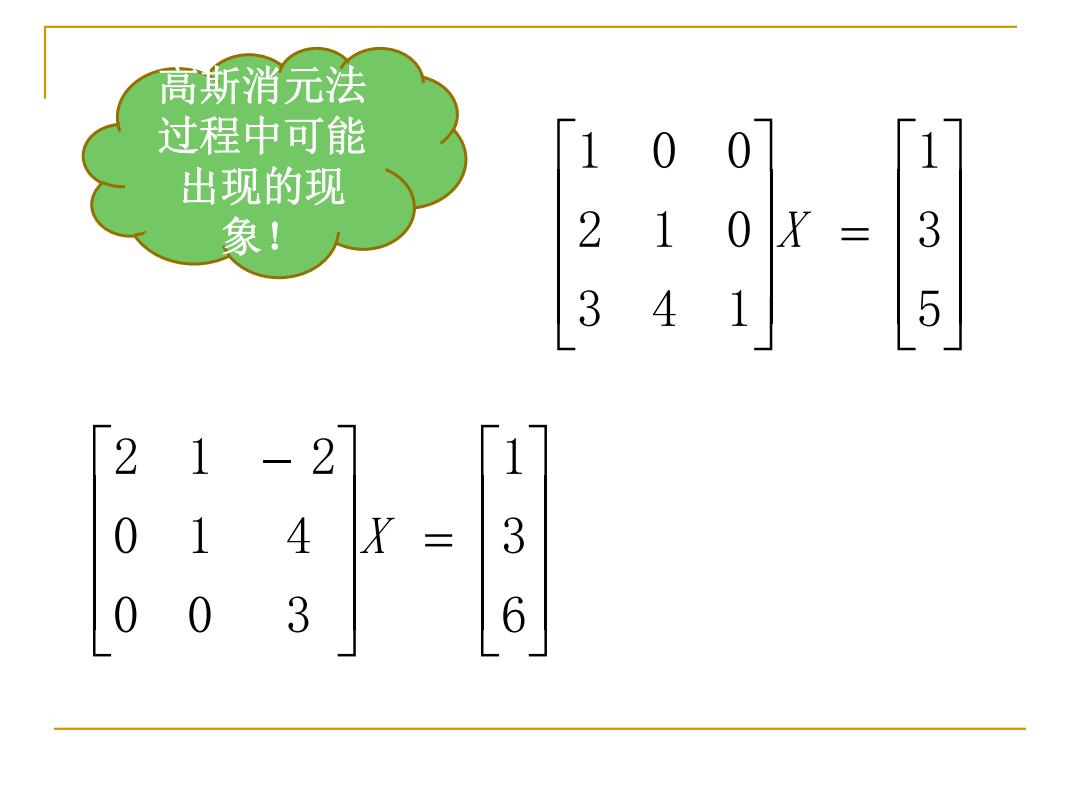
高斯消元法 过程中可能 1 0 0 出现的现 象! 2 1 0 X 三 3 3 4 [5 2 1 2 1 0 1 4 X 三 3 0 3 16
5 3 1 143 012 001 X 6 3 1 300 410 212 X 高斯消元法 过程中可能 出现的现 象!

问题4: 三角阵会给解线性方程 组带来什么便利?