16 运筹学基础及其MATLAB应用 例1.4利用图解法求解线性规划问题: maxz=x1+(3/2)r2 s.t. 2x1+3x2≤16 (1-1-7) 4x1+x2≤12 E1,2≥0 解不难看出,这个线性规划问题与问题(1-1-1)只是目标函数不同。这里的目标 函数与第一个约束直线是平行的,用图解法求解的结果见图1-2。此时,由于目标函数与 约束的边界DE段重复时函数值最大,故此时有无穷多组最优解。最优解x和x吃满足 2x1+3x吃=16,且0≤x1≤2。最优值z*=8。 ⊙ 2*1+3x*2=16,0≤x*1≤2 D 0 4m+=12 2m+3m=16 图1-2图解法求解线性规划问题(1-1-7) 例1.5 利用图解法求解线性规划问题: max z=2x1+2T2 s.t. x1-2≥1 (1-1-8) -x1+2x2≤0 1,x2≥0 解根据上面所说的步骤画出其可行域ABCD,见图1-3。从图上可以看出,可行 域ABCD是无界的。随着目标函数向右上方移动时,目标函数值一直增加,且一直都有 点在可行域里。这就是说,目标函数值(求最大)是无上界的
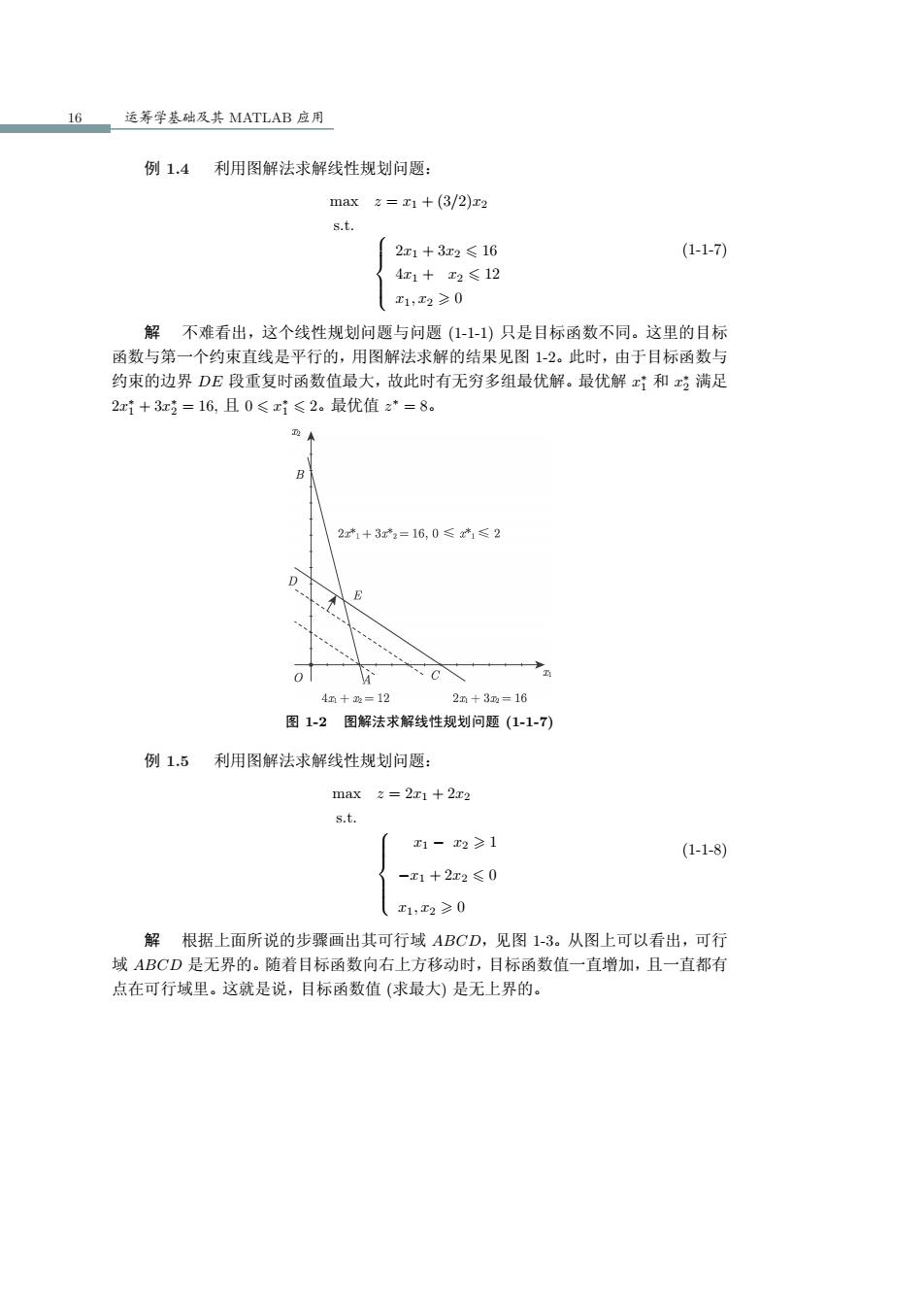
16 运筹学基础及其 MATLAB 应用 例 1.4 利用图解法求解线性规划问题: max z = x1 + (3/2)x2 s.t. 2x1 + 3x2 6 16 4x1 + x2 6 12 x1, x2 > 0 (1-1-7) 解 不难看出,这个线性规划问题与问题 (1-1-1) 只是目标函数不同。这里的目标 函数与第一个约束直线是平行的,用图解法求解的结果见图 1-2。此时,由于目标函数与 约束的边界 DE 段重复时函数值最大,故此时有无穷多组最优解。最优解 x ∗ 1 和 x ∗ 2 满足 2x ∗ 1 + 3x ∗ 2 = 16, 且 0 6 x ∗ 1 6 2。最优值 z ∗ = 8。 图 1-2 图解法求解线性规划问题 (1-1-7) 例 1.5 利用图解法求解线性规划问题: max z = 2x1 + 2x2 s.t. x1 − x2 > 1 −x1 + 2x2 6 0 x1, x2 > 0 (1-1-8) 解 根据上面所说的步骤画出其可行域 ABCD,见图 1-3。从图上可以看出,可行 域 ABCD 是无界的。随着目标函数向右上方移动时,目标函数值一直增加,且一直都有 点在可行域里。这就是说,目标函数值 (求最大) 是无上界的
第1章线性规划及单纯形法17 西-=1 2x+2岁=12 A -五+2=0 1B O0 D 图1-3图解法求解线性规划问题(1-1-8) 例1.6利用图解法求解线性规划问题: max z=1+T2 s.t. -x1+x2≥1 (1-1-9) -x1-2≥1 x1,t2≥0 解根据题设约束条件画出图1-4。从图上可以看出,两个约束条件确定的区域D1 和变量非负的要求矛盾。所以,该问题不存在可行解,即不存在满足两个约束条件的非负 变量x1,c2 --2=1 D -五十2=1 图1-4图解法求解线性规划问题(1-1-9) 上面讨论了线性规划解的4种可能性,即有唯一解、无穷多组解、无界解和无可行 解。值得注意的是,在例1.3中,可行域OAED是一个四边形,最后得到的最优解在其 中的一个顶点上。可行域里面的点都是可行解,在经济学上意味着在可行域OAED中任
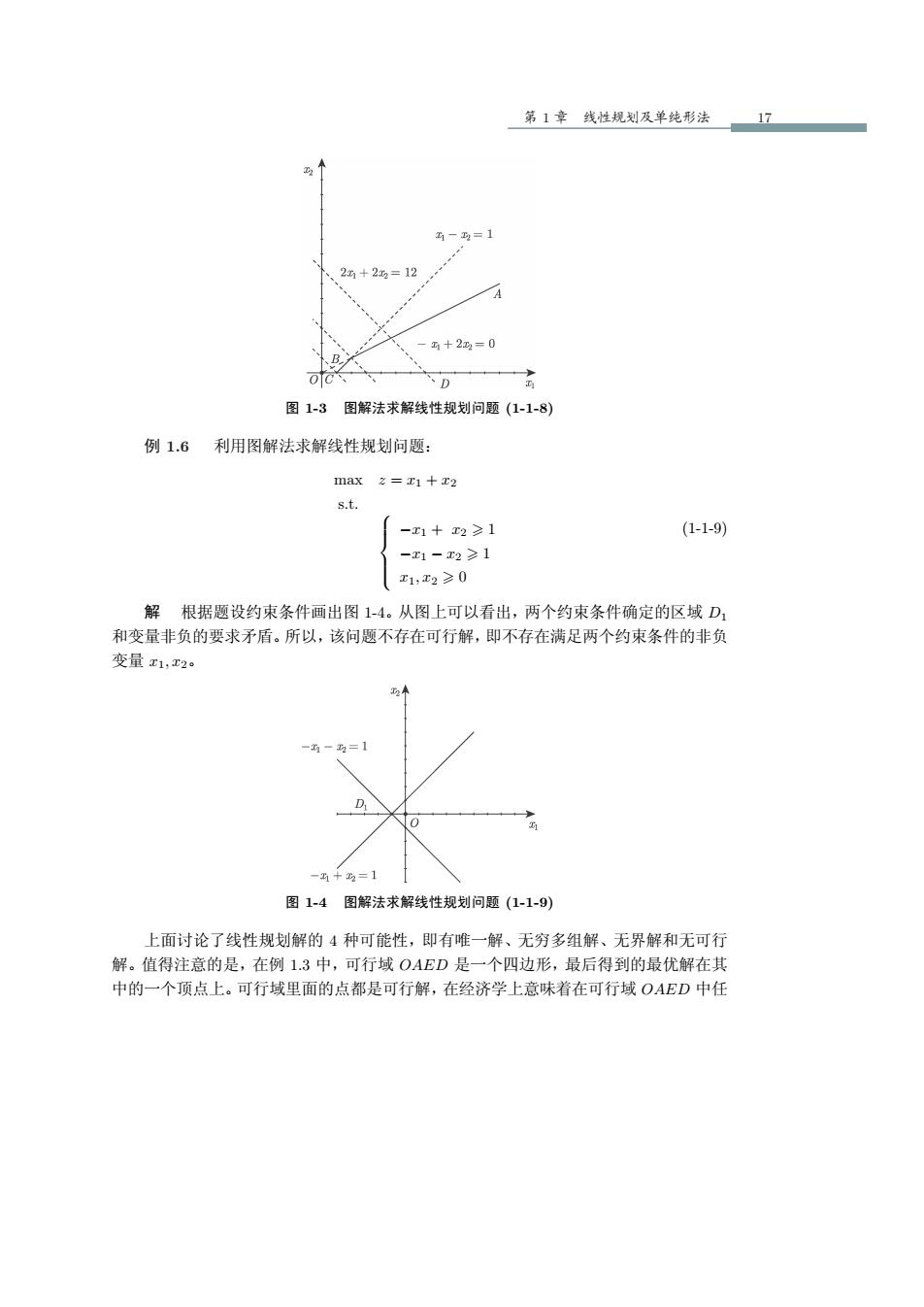
第 1 章 线性规划及单纯形法 17 图 1-3 图解法求解线性规划问题 (1-1-8) 例 1.6 利用图解法求解线性规划问题: max z = x1 + x2 s.t. −x1 + x2 > 1 −x1 − x2 > 1 x1, x2 > 0 (1-1-9) 解 根据题设约束条件画出图 1-4。从图上可以看出,两个约束条件确定的区域 D1 和变量非负的要求矛盾。所以,该问题不存在可行解,即不存在满足两个约束条件的非负 变量 x1, x2。 图 1-4 图解法求解线性规划问题 (1-1-9) 上面讨论了线性规划解的 4 种可能性,即有唯一解、无穷多组解、无界解和无可行 解。值得注意的是,在例 1.3 中,可行域 OAED 是一个四边形,最后得到的最优解在其 中的一个顶点上。可行域里面的点都是可行解,在经济学上意味着在可行域 OAED 中任

18 运筹学基础及其MATLAB应用 选一点进行生产都是可行的(有无穷多个可行点),因为这样的生产没有超出该厂拥有的 资源数量。但最优点(最优生产计划)出现在其可行域的一个顶点上,不是可行域内部的 某个点。这个题目虽然简单,但上述结论却具有一般性。下节将证明线性规划问题的可 行域若有界,则其最优解一定可以在其某个顶点或某段边界上得到。下面继续讨论与线 性规划的解有关的几个概念。 1.可行解、可行域和最优解 满足线性规划问题所有约束条件,包括非负约束的解称为线性规划问题的可行解。 所有可行解组成的集合称为可行域。常常记为D。对于线性规划问题(1-1-6),有 D={XAX=b,X≥0} 从上面的图解法可知,可行域D可能是空集,也可能非空。在非空集时,可能是有界的, 也可能是无界的。每个可行解对应一个目标函数值,在所有目标函数值中最大者或最小 者就是最优解,相应的目标函数值为最优目标函数值。 2.基、基变量、非基和非基变量 考虑线性规划的标准形式(1-1-6),即 max z=cTX S.t. AX=b X≥0 其中,A=(a)mn∈Rmn;c∈R;X=(x1,x2,·,xn)T∈R";b∈Rm。 首先,假设技术系数矩阵A的行数不大于列数,即假设m≤n。实际上,在后面将 会学习到线性规划的对偶理论,根据对偶理论,任何一个线性规划问题(称为原问题)都 有一个对偶线性规划(对偶问题)与之对应,两者有非常密切的联系,且两者的技术系数 矩阵刚好互为转置。所以,当出现了m>n的情况时,可以转而讨论其对偶问题。因此, 这种假设不失一般性。其次,假设rak(A)=m,即假设A是行满秩的。在线性规划的 约束AX=b中,每一个等式对应一个约束条件。假设A行满秩就是假设A的行向量 组是线性无关的,也就是假设不会出现多余的约束条件。因此,这种假设也是合理的。 由于矩阵A的秩总是等于其行向量组的秩,也等于其列向量组的秩,故在上面的两 种假设下,A的n个列向量组成的向量组P1,P2,·,Pn中至少有m个列向量是线性 无关的。称这m个列向量为线性规划约束方程组的一组基。这组基构成约束方程组的一 个子矩阵,记为B。显然,这样的基最多有Cπ组。与基对应的决策变量称为基变量。这 部分决策变量也构成决策向量X的一个部分,记为XB。A中除基以外的其他列向量称
18 运筹学基础及其 MATLAB 应用 选一点进行生产都是可行的 (有无穷多个可行点),因为这样的生产没有超出该厂拥有的 资源数量。但最优点 (最优生产计划) 出现在其可行域的一个顶点上,不是可行域内部的 某个点。这个题目虽然简单,但上述结论却具有一般性。下节将证明线性规划问题的可 行域若有界,则其最优解一定可以在其某个顶点或某段边界上得到。下面继续讨论与线 性规划的解有关的几个概念。 1. 可行解、可行域和最优解 满足线性规划问题所有约束条件,包括非负约束的解称为线性规划问题的可行解。 所有可行解组成的集合称为可行域。常常记为 D。对于线性规划问题 (1-1-6),有 D = {X|AX = b, X > 0} 从上面的图解法可知,可行域 D 可能是空集,也可能非空。在非空集时,可能是有界的, 也可能是无界的。每个可行解对应一个目标函数值,在所有目标函数值中最大者或最小 者就是最优解,相应的目标函数值为最优目标函数值。 2. 基、基变量、非基和非基变量 考虑线性规划的标准形式 (1-1-6),即 max z = c TX s.t. ( AX = b X > 0 其中,A = (aij )m·n ∈ R m·n ; c ∈ R n ; X = (x1, x2, · · · , xn) T ∈ R n ; b ∈ R m。 首先,假设技术系数矩阵 A 的行数不大于列数,即假设 m 6 n。实际上,在后面将 会学习到线性规划的对偶理论,根据对偶理论,任何一个线性规划问题 (称为原问题) 都 有一个对偶线性规划 (对偶问题) 与之对应,两者有非常密切的联系,且两者的技术系数 矩阵刚好互为转置。所以,当出现了 m > n 的情况时,可以转而讨论其对偶问题。因此, 这种假设不失一般性。其次,假设 rank(A) = m,即假设 A 是行满秩的。在线性规划的 约束 AX = b 中,每一个等式对应一个约束条件。假设 A 行满秩就是假设 A 的行向量 组是线性无关的,也就是假设不会出现多余的约束条件。因此,这种假设也是合理的。 由于矩阵 A 的秩总是等于其行向量组的秩,也等于其列向量组的秩,故在上面的两 种假设下,A 的 n 个列向量组成的向量组 P 1, P 2, · · · , P n 中至少有 m 个列向量是线性 无关的。称这 m 个列向量为线性规划约束方程组的一组基。这组基构成约束方程组的一 个子矩阵,记为 B。显然,这样的基最多有 C m n 组。与基对应的决策变量称为基变量。这 部分决策变量也构成决策向量 X 的一个部分,记为 XB。A 中除基以外的其他列向量称

第1章线性规划及单纯形法 19 为非基,它们构成A中除基B以外的部分,记为N。相应的变量称为非基变量,这部 分决策变量记为XN。为叙述方便起见,不妨假设A的前m个列向量是线性无关的(在 理论上总是可以通过对决策变量重新编号来得到,但后面将会发现,实际计算中不需要 这样做),则有 A=(P1,P2,…,Pn)=(B,N),B=(P1,P2,…,Pm),N=(Pm+1,Pm+2,…,Pn) X=(z1,x2,…,xn)T=(XB,XR)T,XB=(a1,E2,…,xm)T,XN=(zm+1,…,xn)T 3.基解、基可行解和可行基 根据上面的讨论,此时由线性规划问题的约束方程组AX=b得到 (B,N) XB =b→BXB+NXN=b→XB=B-b-B-1NXN XN 令非基变量XN=0,则得到XB=B-1b。两项合在一起得到的X=(bTB-T,0)T 称为线性规划的一个基解。显然,基选取的不一样,基解也不一样。其中正好满足X≥0 的基解称为一个基可行解,相应地基B称为可行基。若基解中非零分量的个数少于m 时,称为退化解。 1.1.3线性规划问题的有关结论 上面一节讨论了线性规划的图解法及解的几种可能性,并介绍了一些相关概念,现 在讨论线性规划的有关理论问题。 定义1.1(凸集)设K是n维欧氏空间的一个点集,若对0≤入≤1中的任何一个 入均有 XX)+(1-A)X②∈K,X),X②)∈K 则称K为凸集(Convex Set). 从几何上来说,定义中的AX)+(1-)X②)表示了连接X)和X②)两个点中的 任何一个点,是两点之间的连线段。因此,凸集的“几何形状”是一个中间没有空洞的实 心体。若包含了边界,则为闭凸集;反之,则为开凸集。 定义1.2(凸组合)设X⑧∈R"(位=1,2,·,k),若存在0≤≤1,i=1,2,…,k 且∑:=1使得 i=l X=∑4X@回 =1 则称X为X),X2),·,X)的凸线性组合,简称凸组合
第 1 章 线性规划及单纯形法 19 为非基,它们构成 A 中除基 B 以外的部分,记为 N。相应的变量称为非基变量,这部 分决策变量记为 XN。为叙述方便起见,不妨假设 A 的前 m 个列向量是线性无关的 (在 理论上总是可以通过对决策变量重新编号来得到,但后面将会发现,实际计算中不需要 这样做),则有 A= (P 1, P 2, · · · , P n)= (B, N), B = (P 1, P 2, · · · , P m), N = (P m+1, P m+2, · · · , P n) X = (x1, x2, · · · , xn) T = (XT B, XT N ) T, XB = (x1, x2, · · · , xm) T, XN = (xm+1, · · · , xn) T 3. 基解、基可行解和可行基 根据上面的讨论,此时由线性规划问题的约束方程组 AX = b 得到 (B, N) Ã XB XN ! = b =⇒ BXB + NXN = b =⇒ XB = B −1 b − B −1NXN 令非基变量 XN = 0,则得到 XB = B −1 b。两项合在一起得到的 X = (b TB −T , 0) T 称为线性规划的一个基解。显然,基选取的不一样,基解也不一样。其中正好满足 X > 0 的基解称为一个基可行解,相应地基 B 称为可行基。若基解中非零分量的个数少于 m 时,称为退化解。 1.1.3 线性规划问题的有关结论 上面一节讨论了线性规划的图解法及解的几种可能性,并介绍了一些相关概念,现 在讨论线性规划的有关理论问题。 定义 1.1 (凸集) 设 K 是 n 维欧氏空间的一个点集,若对 0 6 λ 6 1 中的任何一个 λ 均有 λX(1) + (1 − λ)X(2) ∈ K, X(1) , X(2) ∈ K 则称 K 为凸集 (Convex Set)。 从几何上来说,定义中的 λX(1) + (1 − λ)X(2) 表示了连接 X(1) 和 X(2) 两个点中的 任何一个点,是两点之间的连线段。因此,凸集的“几何形状”是一个中间没有空洞的实 心体。若包含了边界,则为闭凸集;反之,则为开凸集。 定义 1.2 (凸组合) 设 X(i) ∈ R n (i = 1, 2, · · · , k),若存在 0 6 µi 6 1, i = 1, 2, · · · , k 且 X k i=1 µi = 1 使得 X = X k i=1 µiX(i) 则称 X 为 X(1) , X(2) , · · · , X(k) 的凸线性组合,简称凸组合