由Q,=Q推得: P:-P=P2 P:=P+p 流量特性曲线 负载压降: PL=P-P2 OL=f(x,)p,=常数的曲线 p=Btp B2-L-2 2 2 当p,=0时,为空载流量 PL=0 负载流量 特性曲线(右图) 1 1 1:零开口 Q.=2-Q:=CA (P.-P)-C,4yb(P.+P) 2:正开口 总供油量 实测流 量曲线 100500 50 电流m、 )承文点人岁 零开口阀流量内泄特性 上活文1大修 压力特性曲线 b 没漏流量Q, PL=f(x,)g,=常数 2 通常指的是 =0时的曲 线 P=const 阀的行程名 1:零开口 2:正开口 在供油压力不变负载流量为零 的情况下,改变阀芯位移,测得 阀芯略微移动,压降就迅速 的供油量: 增加,表明压力增益很高 阀芯在中位时泄漏最大 上潘成1大孝 4.2.3、阀的线性化分析 压力一流量特性方程以增量形 表示的线性化表达式 线性化处理 设某一工作点:Qn=f(Po.x.)o 则在该点附近工作时: 0=(Px,)是一非线性函数。 QL=f(Pu,x,)fPo+pz,x0+△,) 分析之前先线性化。阀通常在工作点附近 工作,因而线性化所带来的误差一般较 0+电 小。 忽略高阶项: Q.-0n=A0,=al△ 6
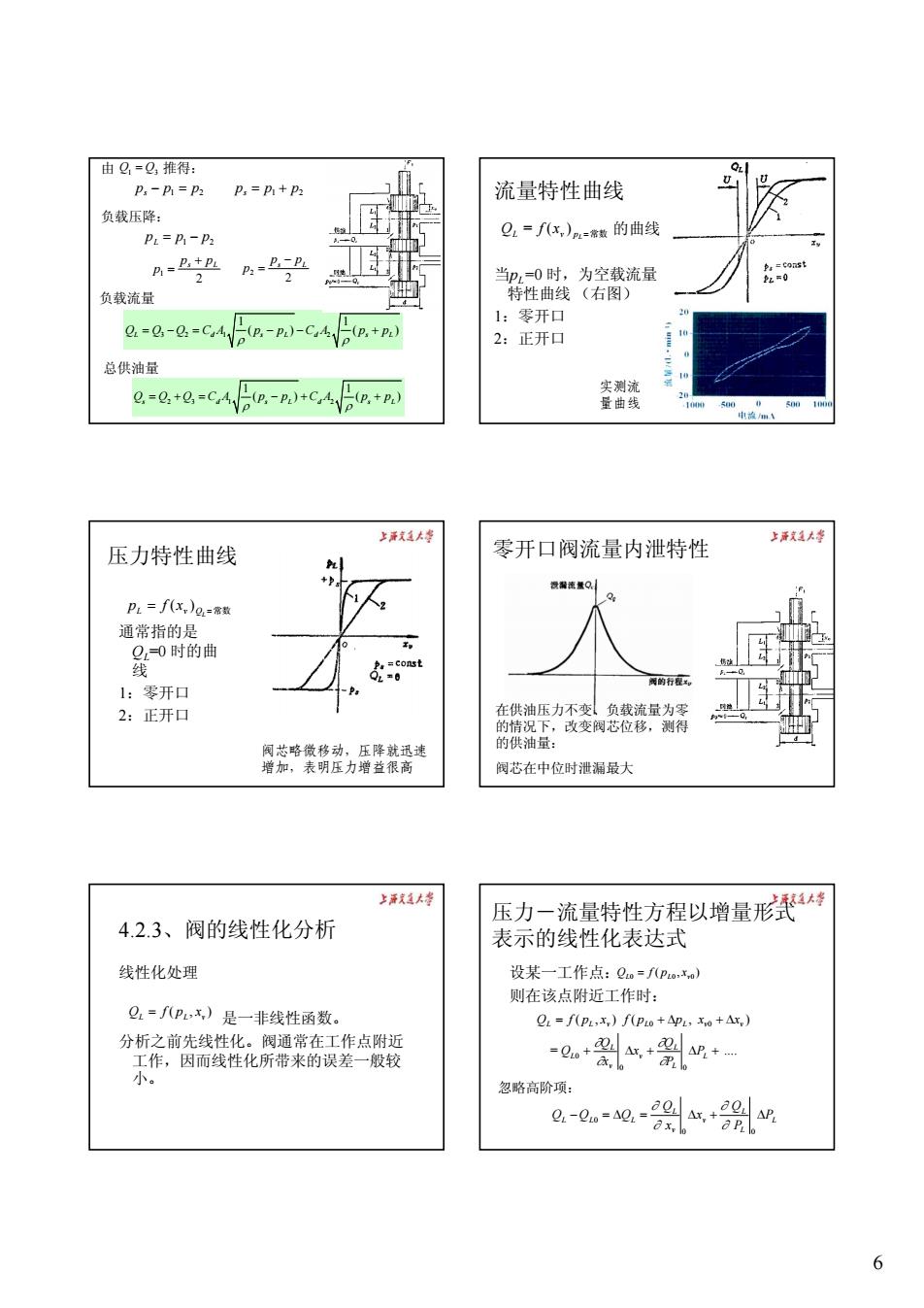
6 1 2 p p p L = − 2 1 ps pL p + = 2 2 ps pL p − = 32 1 2 1 1 () () Q Q Q CA p p CA p p L d sL d sL ρ ρ =−= − − + 23 1 2 1 1 () () Q Q Q CA p p CA p p s d sL d sL ρ ρ =+= − + + ps − p1 = p2 ps = p1 + p2 负载压降: 负载流量 总供油量 由 推得: Q1 = Q3 流量特性曲线 的曲线 当pL=0 时,为空载流量 特性曲线 (右图) 1:零开口 2:正开口 QL = f (xv ) pL =常数 实测流 量曲线 压力特性曲线 通常指的是 QL=0 时的曲 线 1:零开口 2:正开口 pL = f (xv )QL =常数 阀芯略微移动,压降就迅速 增加,表明压力增益很高 零开口阀流量内泄特性 在供油压力不变、负载流量为零 的情况下,改变阀芯位移,测得 的供油量: 阀芯在中位时泄漏最大 4.2.3、阀的线性化分析 线性化处理 是一非线性函数。 分析之前先线性化。阀通常在工作点附近 工作,因而线性化所带来的误差一般较 小。 ( , ) L L v Q = f p x 压力-流量特性方程以增量形式 表示的线性化表达式 设某一工作点: 则在该点附近工作时: ( , ) L0 L0 v0 Q = f p x = .... ( , ) ( , ) 0 0 0 0 0 + Δ + Δ + = + Δ + Δ L L L v v L L L L v L L v v P P Q x x Q Q Q f p x f p p x x ∂ ∂ ∂ ∂ L L L v v L L L L P P Q x x Q Q −Q = ΔQ = Δ + Δ 0 0 0 ∂ ∂ ∂ ∂ 忽略高阶项:
上泽成大坐 上浙克1大当 阀的三个重要系数 阀的线性化流量方程 根据上面定义,压力一流量曲线的线性化 (1)流量增益: K,-20 y 方程变为: (2)流量一压力系数: (3)压力增益: AQ=K,Ax,-K△P opL K=0x. 阀系数随工作点而变,通常以零位工作点的 三系数的关系: 数值计算。此时: K K,0最大,对稳定性最不利: K K. K最小,阻尼比最小,对稳定性也最不利。 在零位稳定,在其他工作点肯定稳定。 屏充1大皆 上活文1大修 4.2.4、 零开口四通滑阀的分析 一、压力一流量特性 讨论对象假设:滑阀为理想滑阀 内容: ◆确定稳态工况下 的负载压力一流 Q,=f八p,儿-骑定值 量关系 ◆阀系数的计算 ? 径向问隙为 零(实际为 PL 1~3u) 工作棱边为锐 边(r=0) 上潘元1大孝 则由 上活丝大举 1 Q:=Q;-O:=CA (P.-P)-Cky -(P,+P:) 可得: .=g-0=C4月-p) 当x,>0时 p,+p) Q,=0-0=-c4 当x<0时 由于A(x,)=A(-x,) d 将Q二式合并成一式,有: 当x,>0时,42=A4=0,即Q2=Q4=0 当x,<0时,A1=A3=0,即Q,=Q3=0 7
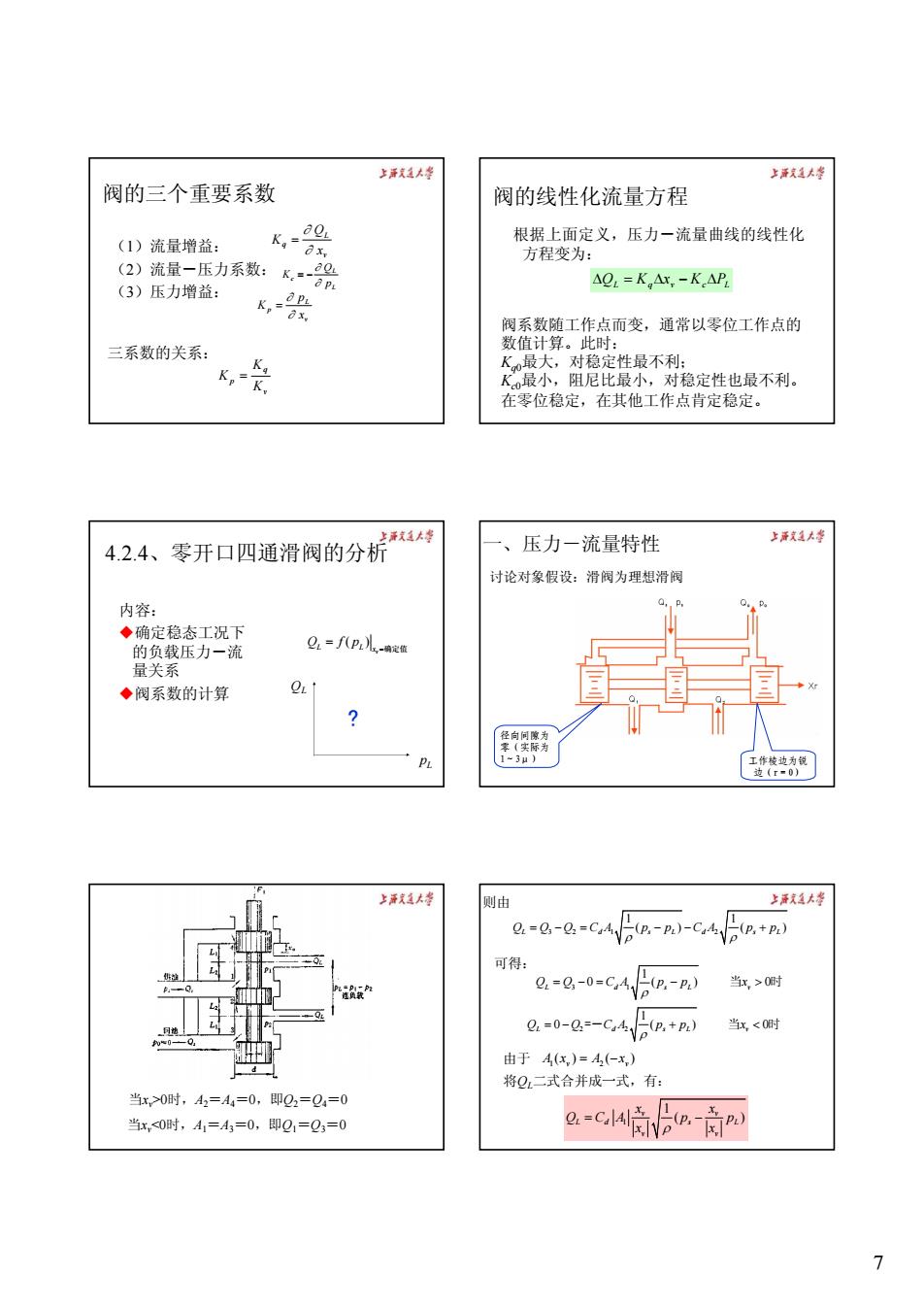
7 阀的三个重要系数 (1)流量增益: (2)流量-压力系数: (3)压力增益: v L q x Q K ∂ ∂ = L L c p Q K ∂ ∂ = − v L p x p K ∂ ∂ = v q p K K K = 三系数的关系: 阀的线性化流量方程 根据上面定义,压力-流量曲线的线性化 方程变为: L q v Kc PL ΔQ = K Δx − Δ 阀系数随工作点而变,通常以零位工作点的 数值计算。此时: Kq0最大,对稳定性最不利; Kc0最小,阻尼比最小,对稳定性也最不利。 在零位稳定,在其他工作点肯定稳定。 4.2.4、零开口四通滑阀的分析 内容: 确定稳态工况下 的负载压力-流 量关系 阀系数的计算 ( ) v L L x Q fp = = 确定值 QL pL ? 一、压力-流量特性 讨论对象假设:滑阀为理想滑阀 径向间隙为 零(实际为 1~3μ) 工作棱边为锐 边(r=0) 当xv>0时,A2=A4=0,即Q2=Q4=0 当xv<0时,A1=A3=0,即Q1=Q3=0 32 1 2 1 1 () () Q Q Q CA p p CA p p L d sL d sL ρ ρ =−= − − + 则由 可得: 将QL二式合并成一式,有: 3 1 1 0 () 0 Q Q CA p p x L d sL v ρ = −= − > 当 时 2 2 1 0 () 0 Q Q CA p p x L d sL v ρ =− + < =- 当 时 1 1 ( ) v v L d sL v v x x Q CA p p x x ρ = − ( ) ( ) 1 v 2 v 由于 A x = A −x

稳态特性方程 上泽成大坐 上浙克1大当 上面两式相除: 若节流窗口为矩形(包括全周),则A=wx, 其中w为面积梯度(m)。 9 x,PL 则有: x p. 为了能用无因次形式表示,设pL=O和x,=xma时的 可得=f(PL)x花数 最大空载流为: 压力一流量特性曲线,其为 抛物线线族 零开口压力一流量特性曲线 )承文点人岁 阀的三系数 上活文1大修 QL=f(PL)m常数 ◆正常工作区为1.Ⅲ象限 对稳态特性方程求偏微分,可得: ◆因阀的节流口匹配对称,故 影响开 白线对称于原点 ◆当PL印,<23时,线性度 流量增益:K。= 0L=c (P,-P) 冫环增益 Ox. 较好,实际也多工作在此苑 ◆聚我纯药品的于成线性 流量一压力系数: 影响刚 特性曲线表明了什么? K.--00 [L(p.-PD) 度和阻 2(P,-P) 尼 ◆最大开度下的压力-流量特 0. 性曲线可表示阀的工作能力和 =0.8 规格。 K_2(P,-PL) 影响票动负载 ◆当负载所需的压力和流量能 压力增益:K。= 够被曲线包图时,阀就能满足 Ke 的能力和负载 引起的误差 负载的要求 上潘元1大孝 上活丝大举 零位阀系数 Ko和o的实际计算 条件:Q=P2=x,=0 根据流体力学理论分析,对于无限平 面上高为b、宽为o,而且w>b的 此时的阀系数为: 矩形锐边节流孔,在层流状态下通 K0=c01 Ps 过该孔的流量可用下式确定: K0=0 后两个系数与实 0= -△p 际试验不符,另 32 K0=0 有实际求法 式中,△p:节流孔两边的压力差 μ:液体的动力粘度 8
8 稳态特性方程 1 ( ) v L dv s L v x Q Cx p p x ω ρ = − max max s L dv p Q Cx ω ρ = 为了能用无因次形式表示,设pL=0和xv= xvmax时的 最大空载流为: 若节流窗口为矩形(包括全周),则A1=ωxv, 其中ω为面积梯度(m)。 则有: 上面两式相除: max max 1 L v v L L v vs Q p x x Q x xp = − ⋅ 可得 压力-流量特性曲线,其为 抛物线线族 QL = f ( pL )Xv =常数 零开口压力-流量特性曲线 QL = f ( pL ) Xv =常数 正常工作区为I、III象限 因阀的节流口匹配对称,故 曲线对称于原点 当 pL /ps ≤ 2/3 时,线性度 较好,实际也多工作在此范 围 pL=常数时,QL与xv成线性 关系(矩形窗口时) 特性曲线表明了什么? 最大开度下的压力-流量特 性曲线可表示阀的工作能力和 规格。 当负载所需的压力和流量能 够被曲线包围时,阀就能满足 负载的要求 阀的三系数 对稳态特性方程求偏微分,可得: 1 ( ) L q d sL v Q K c pp x ω ρ ∂ == − ∂ 1 ( ) 2( ) dv s L L c L sL cx p p Q K p pp ω ρ − −∂ = = ∂ − q 2( ) s L p c v K p p K K x − 压力增益: = = 流量-压力系数: 流量增益: 影响开 环增益 影响驱动负载 的能力和负载 引起的误差 影响刚 度和阻 尼 零位阀系数 条件: 此时的阀系数为: 0 Qpx L Lv = == 后两个系数与实 际试验不符,另 有实际求法 0 s q d p K c ω ρ = 0 0 Kc = Kp0 = ∞ Kc0和Kp0的实际计算 根据流体力学理论分析,对于无限平 面上高为b、宽为ω,而且ω>>b的 矩形锐边节流孔,在层流状态下通 过该孔的流量可用下式确定: 2 32 b Q p π ω μ = Δ 式中,△p:节流孔两边的压力差 μ:液体的动力粘度