吉林大学：《土质学与土力学》课程电子教案（PPT课件）第5章 地基中的应力计算

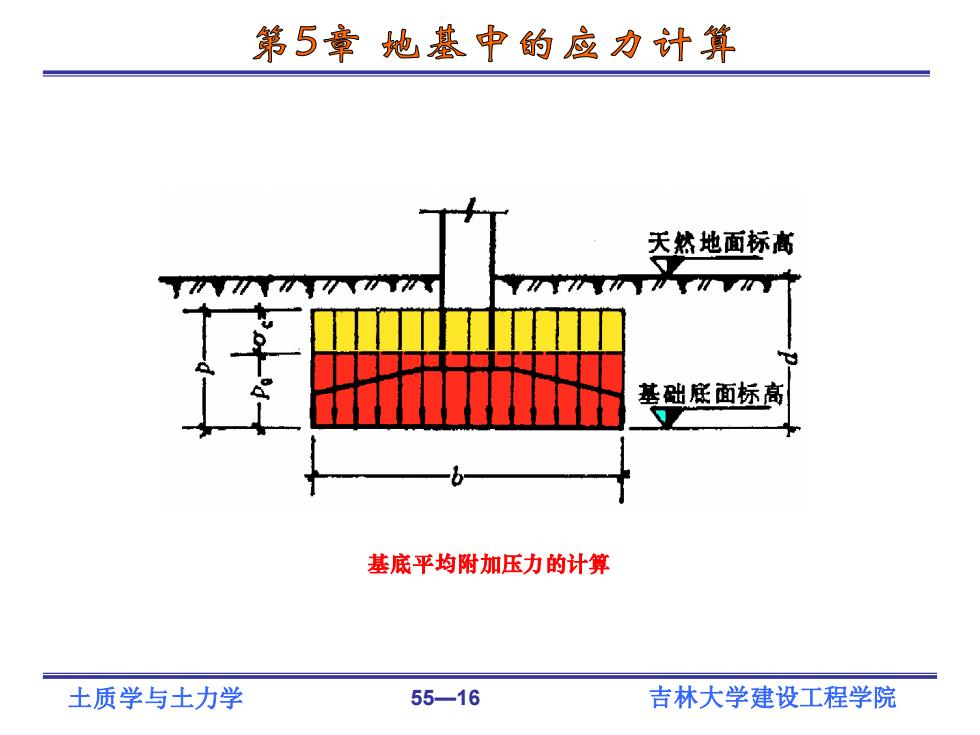
第5章地基中的应力计算 天然地面标高 基础底面标高 基底平均附加压力的计算 土质学与土力学 55-16 吉林大学建设工程学院

土质学与土力学 55—16 吉林大学建设工程学院 基底平均附加压力的计算

第5章地基中的应力计算 5.4地基附加应力 地基附加应力是指建筑物荷重在土体中引起的附加于原有应力之上的 应力。它是使地基产生变形和引起建筑物沉降的主要原因。 地基附加应力计算的假定 (1)地基土是均质、各向同性的半无限空间线弹性体。 (2)直接采用弹性力学理论解答。 (3)基底压力是柔性荷载，不考虑基础刚度的影响。 叠加原理 叠加原理建立在弹性理论基础之上，当地基表面同时作用有几个力时， 可分别计算每一个力在地基中引起的附加应力，然后每一个力在地基中引 起的附加应力累加求出附加应力的总和。 土质学与土力学 55-17 吉林大学建设工程学院

土质学与土力学 55—17 吉林大学建设工程学院 地基附加应力是指建筑物荷重在土体中引起的附加于原有应力之上的 应力。它是使地基产生变形和引起建筑物沉降的主要原因。 地基附加应力计算的假定 (1) 地基土是均质、各向同性的半无限空间线弹性体。 (2) 直接采用弹性力学理论解答。 (3) 基底压力是柔性荷载，不考虑基础刚度的影响。 叠加原理 叠加原理建立在弹性理论基础之上，当地基表面同时作用有几个力时， 可分别计算每一个力在地基中引起的附加应力，然后每一个力在地基中引 起的附加应力累加求出附加应力的总和。 5.4 地基附加应力

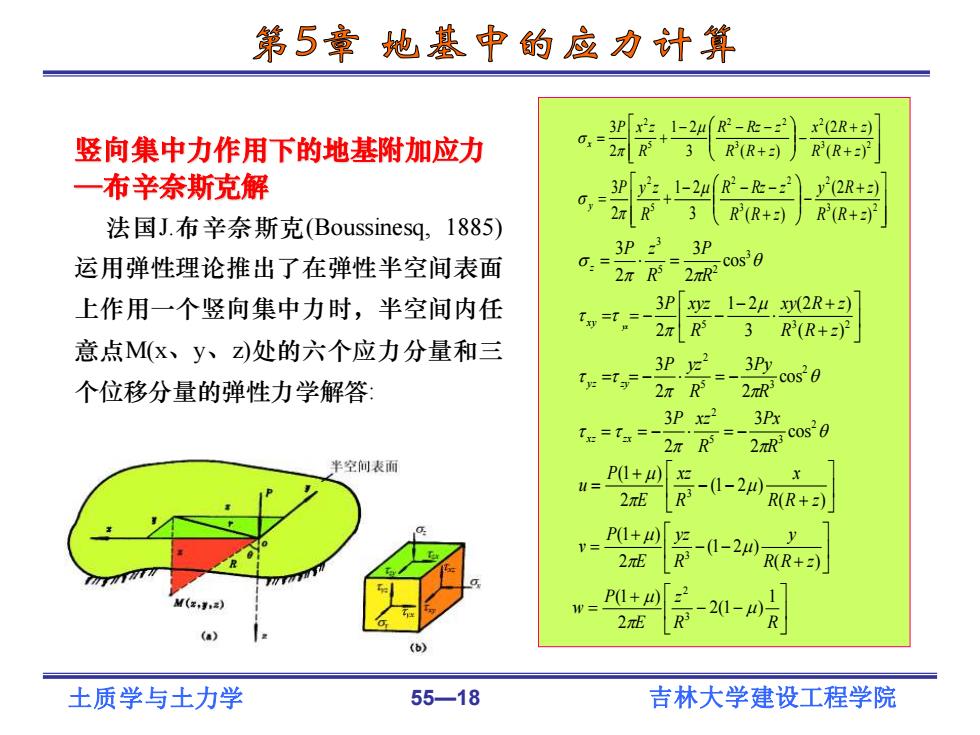
第5章地基中的应力计算 竖向集中力作用下的地基附加应力 。=,上2-- x2(2R+z) 2元R 3R(R+) R(R+) 一布辛奈斯克解 3P2:1-24R2-e- y2(2R+ 法国J.布辛奈斯克(Boussinesq,.1885) 2x R 3 R(R+2) R(R+)2 3P33P 运用弹性理论推出了在弹性半空间表面 0= os0 2πR2πR2 上作用一个竖向集中力时，半空间内任 3Pz1-242R+z) 2πR 3 R(R+z) 意点M(x、y2)处的六个应力分量和三 3P y2 3Py 个位移分量的弹性力学解答 2n R 2zk cosg Tx=fa-- 3P xz2 3Px πR 2xB cos0 半空间表而 P(1+u)xz l= -1-20 R(R+2) P(1+u)y y V= 2πER -(1-20） R(R+z) M(x,,) w=P+四[2 -21-川 2nE P (a 土质学与土力学 55-18 吉林大学建设工程学院

土质学与土力学 55—18 吉林大学建设工程学院        + + −         + − − − = + 3 2 2 3 2 2 5 2 ( ) (2 ) 3 ( ) 1 2 2 3 R R z x R z R R z R Rz z R P x z x            + + −         + − − − = + 3 2 2 3 2 2 5 2 ( ) (2 ) 3 ( ) 1 2 2 3 R R z y R z R R z R Rz z R P y z y        3 5 2 3 cos 2 3 2 3 R P R P z z =  =       + +  − = = − − 5 3 2 ( ) (2 ) 3 1 2 2 3 R R z xy R z R P xyz yx x y          2 5 3 2 cos 2 3 2 3 R Py R P yz yz = zy = −  = −      2 5 3 2 cos 2 3 2 3 R Px R P xz xz = zx = −  = −       + − − + = ( ) (1 2 ) 2 (1 ) 3 R R z x R xz E P u          + − − + = ( ) (1 2 ) 2 (1 ) 3 R R z y R yz E P v          − − + = R R z E P w 1 2(1 ) 2 (1 ) 3 2    竖向集中力作用下的地基附加应力 ─布辛奈斯克解 法国J.布辛奈斯克(Boussinesq, 1885) 运用弹性理论推出了在弹性半空间表面 上作用一个竖向集中力时，半空间内任 意点M(x、y、z)处的六个应力分量和三 个位移分量的弹性力学解答: