
Theorem 1.6 If a graph G contains a u-v walk of length l,then G contains a u-v path of length at most I. Proof.Among all u-vwalks in G,let P=(u=40,1,,uk=V) 还有其它证 be a u-vwalk of smallest length k.Therefore,k sI.We claim that p is a u-v path. 明方法吗? Assume,to the contrary,that this is not the case.Then some vertex of Gmust be repeated in P,sayufor some iandjwithssk.If we then delete the verticesu 2.from P,we arrive at the u-vwalk 图中定理的证 (u=0,1,,1-1,4=j,uj+1,…,4以=V) 明,多用如此 whose length is less than k,which is impossible.Therefore,as claimed,P is a u-vpath 的反证法、构 of length k≤l ■ 造法
图中定理的证 明,多用如此 的反证法、构 造法 v 还有其它证 明方法吗?

图的连通性是图结构的重要特性 Theorem 1.10 Let G be a graph of order 3 or more.Then G is connected if and only if G contains two distinct vertices u and y such that G-u and G-y are connected. Theorem 1.8 Let G be a graph of order 3 or more.If G contains two distinct vertices u and y such that G-u and G -v are connected,then G itself is conected. Theorem 1.9 If G is a connected graph of order 3 or more, then G contains two distinct vertices u and v such that G-u and G-v are connected. 这个定理给了你什么直观感觉?
图的连通性是图结构的重要特性 这个定理给了你什么直观感觉?
定理1.8证明 ·如何证明一个图是连通的? ·任取两个点,证明其连通! ·任取{x,y}两点: ·{x,y}=/={u, ·假设u不是x,y,y一定在G-u中 ·{x,y}={u,v} ·假设x是u,y是v -V ·存在第三点w ●u ow ●w
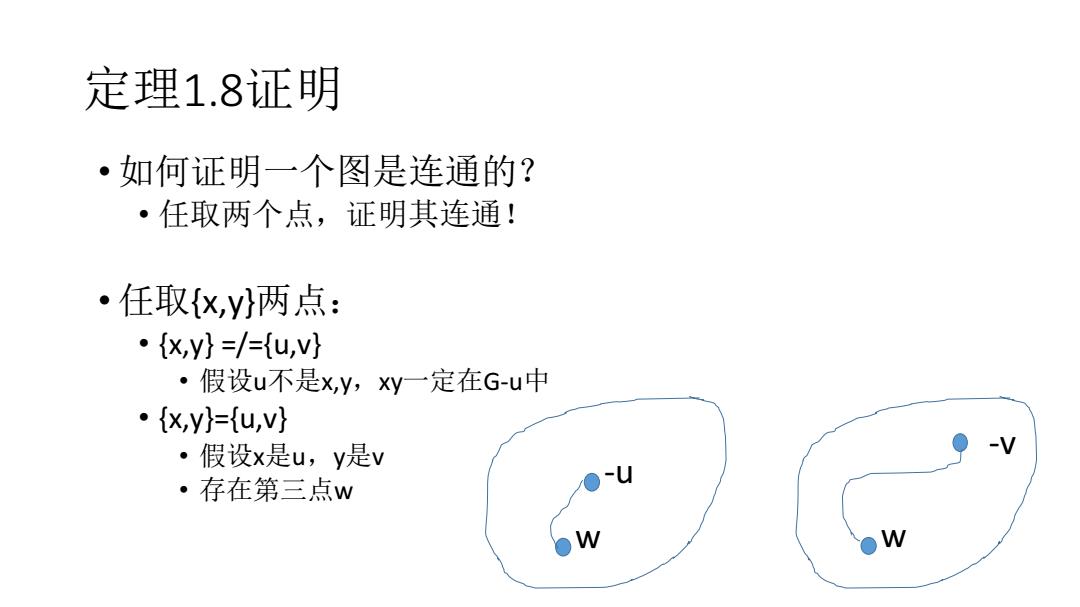
定理1.8证明 • 如何证明一个图是连通的? • 任取两个点,证明其连通! • 任取{x,y}两点: • {x,y} =/={u,v} • 假设u不是x,y,xy一定在G-u中 • {x,y}={u,v} • 假设x是u,y是v • 存在第三点w - u - v w w