
第6卷第6期 智能系统学报 Vol.6 No.6 2011年12月 CAAI Transactions on Intelligent Systems Dec.2011 doi:10.3969/j.issn.16734785.2011.06.009 SPCA参数对单样本人脸识别效果影响分析 王科俊,邹国锋,张洁 (哈尔滨工程大学自动化学院,黑龙江哈尔滨150001) 摘要:奇异值扰动的主分量分析(SPCA)是一种有效的单样本人脸识别方法,但SPCA算法的识别效果受参数选择 的影响比较大,针对SPCA算法中衍生图像生成参数和结合参数a的不同取值对识别效果的影响进行了分析,利 用ORL人脸库和CAS-PEAL人脸库做了大量的实验和比较分析,实验结果表明给出的SPCA参数选取方法和取值范 围是合理的,并有效地提高了SPCA算法的实际应用效果和单样本人脸识别的性能. 关键词:人脸识别;奇异值分解;结合投影主分量分析;奇异值扰动主分量分析;衍生图像;结合图像 中图分类号:TP391.4文献标志码:A文章编号:16734785(2011)06053108 Analysis of the influence of SPCA parameters on the recognition of a single sample face WANG Kejun,ZOU Guofeng,ZHANG Jie (College of Automation,Harbin Engineering University,Harbin 150001,China) Abstract:Singular value decomposition perturbation principal component analysis (SPCA)is an effective single- sample face recognition method;however,the identification results of the SPCA algorithm are seriously affected by parameter selection.In this paper,the effect on the identification,which was caused by the derived image parame- ter and the combined image generation parameter in the SPCA algorithm,was analyzed.Many experiments and comparative analyses were performed on the basis of the ORL face database and the CAS-PEAL face database.The experimental results show that the SPCA parameter selection method and the parameter range given in this paper are reasonable.In addition,reasonable parameters are effective in improving practical application of SPCA algorithms and the recognition performance of a single-sample face. Keywords:face recognition;singular value decomposition;(PC)2A;SPCA;derived image;combined image 单样本人脸识别问题口给人脸识别技术带来人脸识别问题进行了研究,王科俊等2]将目前文献 巨大挑战,近年来已成为人脸识别研究中的一个重 中出现的主要针对单训练样本人脸识别的方法概括 要方向,并得到广泛关注.单样本人脸识别可以有效 为以下几类:基于几何特征的方法、样本扩法、特 降低训练样本的收集成本和存储成本,加快人脸识 征子空间扩展法、通用学习框架法、图像增强法、神 别系统的处理速度,所以在犯罪取证、身份证验证、 经网络法和三维识别方法等.其中,图像增强法是使 银行和海关监控等一些特殊的场合得到应用;但是 那些对于识别比较重要的特征更加突显出来,同时 由于训练样本的有限性,单样本人脸识别的识别率 对那些次要无用的、甚至对识别造成干扰的信息进 往往不高,所以如何有效提高单样本条件下的识别 行抑制的一种方法,该方法侧重于图像的预处理.基 率已成为人们研究的重点· 于奇异值扰动的主分量分析a)](singular value de- 近年来,研究人员分别从不同的角度对单样本 composition perturbation principal component analysis, SPCA)就是利用原图像奇异值分解(singular value 收稿日期:2010-09-14. decomposition,SVD)的重构图像来增强原图像的一 基金项目:国家“863”计划资助项目(2008AA01Z148) 种方法,通过增强能够使样本提供的信息得到充分 利用,可以有效提高识别率,特别是在单样本人脸库 通信作者:邹国锋.E-mai:g841122@163.com, 中人脸类别比较多的情况下效果更显著.SPCA人

·532 智能系统学报 第6卷 脸识别方法易受人脸图像大小影响,随着人脸图像 的不断变小,SPCA方法和其他人脸识别方法的区 V(x)=∑P(x,y) (2) 别变得并不那么明显,同时,SPCA方法也受到衍生 式(1)、(2)的2个投影在一定程度上反映了人脸图 图像重构参数和结合参数的严重影响,但是这2个 像重要局部区域的分布特点。 参数的取值目前还没有可依据的理论方法。 P(x,y)的投影图像定义为 针对SPCA人脸识别方法易受到奇异值分解参 M2(x,y)= V (x)H(y) 数和结合图像生成参数影响的问题,本文就这2个 N NP 参数的取值方法进行了深入分析,同时为了充分讨 式中:P是图像的灰度均值,也即 论这2个参数的影响,在ORL人脸库和CAS-PEAL N1 N2 ∑∑P(x,y) 人脸库上进行了大量实验,验证了不同取值方式对 P= 米=1y 于识别效果产生的不同影响,得出了SPCA人脸识 NN2 别方法中参数取值的原则和规律,为SP℃A在人脸 最后,定义P(x,y)的结合投影图像P(x,y). 识别中的进一步应用提供了参考依据 P(x,y)= P(x,y)+aM(x,y) 1+a 1奇异值扰动的主分量分析法(SPCA) 式中:0<a<1.0为结合参数,P.(x,y)的取值有可 主分量分析法(principal component analysis, 能超出[0,1],可对其进行归一化使其取值在[0,1] PCA)[4由Kiby和Sirovich1首先引入人脸识别,并取 内,归一化策略如下: 得巨大成功,成为一个判别人脸识别方法性能好坏的 P(x,y)= P.(x,y)-min(P.(x,y) max(P.(x,y))-min(P.(x,y)) 公认基准.针对单训练样本人脸识别问题,Wu和 Zhou[6在PCA的基础上提出了结合投影的主分量分 (3) (projection combined principal component analysis, 最后,得到原图像的结合投影图像P(x,y),然 (P℃)2A),这种方法能够在一个更小的特征空间中获 后对其运用P℃A进行降维和特征提取.根据文献 得优于传统PCA算法的识别性能,但是Chen等]又 [6],在使用较少的特征脸(10%~15%)情况下,即 进一步探讨了n阶(P℃)2A,他们认为采用高阶投影组 在一个更小的特征空间中,(PC)2A可以获得比传 合能够进一步降低特征维数,而识别性能略有提高,并 统特征脸方法更高的识别精度, 提出了E(PC)2A(enhanced(PC)2A)算法,随后 1.2奇异值扰动的主分量分析法 Z☑hag等31又注意到人脸图像矩阵的奇异值除了对噪 遵循(PC)2A的思路,SPCA为研究单样本人脸 声不敏感外,还具有保持输入向量的某些代数和几何 识别问题提供了一条新的思路,它是一种图像增强 不变性的重要性质,从而提出了奇异值扰动的主分量 的方法.它首先需要得到图像的奇异值扰动衍生图 像,再把原图像和衍生图像按一定的法则结合形成 singular value decomposition perturbation principal component analysis,SPCA) 结合图像,最后对结合图像运用PCA以识别图像. 1.1结合投影的主分量分析法 SPCA的目的就是要从单幅人脸图像中“挤出”更多 (P℃)2A是专门针对单样本人脸识别提出的,侧 的信息,这些“挤出”的信息包含某些对识别很重要 重图像预处理的一种扩展的P℃A方法,该方法把原 的人脸特征. 人脸图像与其一阶投影相结合,以增强人脸图像中对 假设I(x,y)是一幅归一化的大小为N1×N2的 识别有利的信息,抑制人脸图像中对识别无用的信 图像灰度矩阵,其中I(x,y)∈[0,1],根据奇异值分 息,从而提高单训练样本情况下的人脸识别效果 解定理,I可表示为 假设P(x,y)是一幅经过归一化的大小为N,× I=UAV N2的图像的灰度矩阵,x∈[1,N,],y∈[1,N2], 式中:A是由I的奇异值组成的N×N2阶对角矩 P(x,y)∈[0,1].P(x,y)的水平和垂直投影分别定 ∫入≥0,i=j 义如式(1)和式(2): 阵,它的元素入{0,i U是N×N,阶正交 矩阵,V是N2×N2阶正交矩阵,U和V分别是矩阵 H,(y)=P(x,y), (1) = 和矩阵严I对应于特征值入的特征向量, 然后,通过扰动原图像I的奇异值来获得I的

第6期 王科俊,等:SPCA参数对单样本人脸识别效果影响分析 ·533· 奇异值衍生图像P,P定义为 是n越大越好,当n取较大值时衍生图像的内部信 P=UA"VT (4) 息结构被扰乱,图像变得平滑模糊,不再适合用来表 式中:n是一个实数,取值范围为1<n<2. 征人脸图像,会导致识别率下降,所以在一些文献中 得到衍生图像P后,再把P与原图像I线性结合, 把参数n的变化范围限制在1~2,其中文献[3]通 产生一幅新的结合图像J(x,y),结合方式如式(5): 过定义n=1+1/(11-m)(m=1,2,…,10)将n的 J(x,y)=x,)+aP(x,y 取值设定在1~2,但是这种取值方式使得n的取值 1+ (5) 在m取1~5的数时过于密集,而当m在7~10变 式中:α是结合参数,取值范围为0<a<1.0. 化时n的取值又过于稀疏.当m取1~5的数时,n 通过式(4)求取衍生图像的过程实质是图像重 的取值分别为1.1、1.1111、1.125、1.143、1.1667, 构的过程,当n=1时,衍生图像P等于原始图像I; 显然,参数n这样的取值变化较小,对于奇异值衍生 当n>1时,满足入:>1的奇异值对应的特征向量将 图像的生成不会产生明显的影响变化,从而对于最 被放大,同时入:<1的奇异值所对应的特征向量被 终结合图像增强效果的影响也并不明显,不利于分 缩小,因此衍生图像P在强调较大奇异值作用的同 析n的变化给识别率所带来的影响;而当m取值为 时,对较小的奇异值进行了限制,实现了对人脸图像 7时,n的取值为1.25,当m的取值为8时,n对应的 中有用信息的放大增强,对无用信息的削弱衰减.所 为1.333,当m变化到9的时候n的取值为1.5,所 以,将P结合到I得到结合图像J的这一过程,在保 以中间的取值1.4对于识别效果有怎么样的影响无 持原始图像主要信息的前提下,将会对轻微的表情、 法进行有效的分析. 光照和遮挡等变化具有较好的适应性, 本文对文献[3]中n值的取值方式进行了改 结合图像J(x,y)的取值有可能超出[0,1],尽 进,采取均匀取值的方式,定义n取值为1.1,1.2, 管这对最终的识别结果不会有影响,但显示图像时 …,1.9,2.0,这样可以更全面和均衡准确地分析出 会产生变形.为此,对J(x,y)的取值也采用式(3) 取值分布对于识别率的影响.另外,对参数的取值 进行归一化.然后,对归一化后的结合图像J(x,y) 范围,分别在ORL人脸库和CAS_PEAL人脸库上进 而不是原图像I(x,y)采用主分量分析法提取特征 行了大量的实验,实验表明文献[3]将参数n的上 和识别,这就是奇异值扰动的主分量分析法,也即 限值确定在2.0是并不合理的,在实际的人脸识别 系统中应当根据具体采用的人脸数据库中,人脸图 SPCA. 1.3SPCA参数选取分析 像模式的复杂程度设定参数n的上限值,而将参数 n固定在某一个值的做法是不恰当的. 通过1.2节的分析,可以看出参数n和a对 而对于结合参数α会对识别率产生怎么样的 SPCA过程及识别效果有严重的影响.文献[3]在介 影响,文献[3]中没有给出明确的取值原则,本文则 绍SPCA算法的过程中,将参数a的值设定为0.25, 通过大量的实验对比得出了结合参数α合理的取 但并没有给出取值的原则和方法,只是在参数α= 值范围.在获得参数n和α较小的取值范围后,再在 0.25的情况下简要讨论了参数n对识别效果的影 这个小范围内进行更为精确细致的实验,最终得到 响,得出了n取3/2时SPCA效果较好的结论.另 参数n和a的最优取值, 外,何家忠等8]在讨论一种新的图像增强方法时, 也对参数的取值进行了分析,但也只是在固定α= 2SPCA算法的实现步骤 0.3的情况下分析了参数n的变化带来的影响,并 SPCA算法的实质是奇异值分解结合主分量分 得出n取9/8时算法的识别性能较好,然后在固定 析,因此可连接图像的奇异值分解及主分量分析2 n=9/8时分析了参数α对算法性能的影响,得出了 个步骤来实现,具体实现步骤如下: 参数x的取值范围为0.15<a<0.4.显然,固定一 1)对于人脸库中的一幅人脸图像,可用实矩阵 个参数而分析另一个参数对SPCA过程及识别效果 A∈RMx来表示,先把A的像素值范围归一到[O, 的影响是不全面的,应当在参数n和α同时变化的 1],计算ATA∈RxN 情况下进行有效的分析. 2)利用雅可比过关法[9求出ATA的特征值入: 文献[3]指出在衍生图像的重构过程中参数n (i=1,2,…,W)及对应的特征向量",根据4= 是一个大于1的实数,n取大于1的实数可以有效 1 二Ay:求AAT的特征向量, 地将有用信息进行增强,无用信息进行衰减,但并不 /

·534 智能系统学报 第6卷 3)根据式(4)计算A的奇异值扰动衍生图像 P,根据式(5)和(3)计算结合图像J. 4)将J按列连接成一个M×N维的列向量x:, 用“=2,计算x的均值向量 5)由于计算协方差矩阵Σ=上龙 K2-)( 4)T=ZZ的特征值和特征向量较难,转而计算协方 差”=ZZ和其特征值和特征向量, 图1ORL人脸库中一个人的图像 Fig.1 One person's images in ORL face database 6)根据么,=人2,求协方差矩阵Σ=是 3.2ORL人脸库上的实验结果分析 √: 客(x-)(x-)'=zZ的特征值和特征向量,按 针对参数n和a取不同值,采用文献[3]中的 取值方式和本文提出的均匀取值方式进行了实验, 从大到小的顺序对Σ的特征值及对应的特征向量 图2和图3分别给出了2种取值情况下图像的奇异 排序,然后采用三A,/名入:≥9舍弃无用的特征值和 值扰动衍生图像、结合图像随n变化的情况 其对应的特征向量,得到所需的投影矩阵U, 7)训练图像和测试图像按P=Y往投影空间 U投影,得到投影向量,再利用欧式距离来确定测试 图像的类别。 3 实验结果分析 本文分别在ORL人脸库和CAS-PEAL人脸库 m=7 m=8 m=10 上进行了大量的实验,其中OL人脸库是一个变化 (a)x=0.25时的衍生图像 模式相对单一且由西方人人脸构成的人脸库,而 CAS-PEAL人脸库是变化模式相对较为复杂且由东 方人人脸组成的人脸库,通过在这样的2个人脸库 上的实验可以更充分地验证参数n和α取不同值时 原图像 m=】 m=2 1=3 对SPCA识别效果的影响. 3.10RL人脸库介绍 实验所用人脸图像为英国剑桥大学AT&T实验 m=7 m=8 m=9 m=10 室创建的ORL人脸数据库o].ORL人脸库包括40 (b)a=0.25时的结合图像 个人,每人10幅,共400幅人脸图像,图像为256级 图2文献[3]中m取不同值时的衍生图像和结 灰度,尺寸大小为92×112(宽×高)像素.照片拍摄 合图像 于不同的时间,采用统一的黑色均匀背景,在一定范 Fig.2 The derived images and combined images 围内存在光照变化,面部表情变化(睁眼或者闭眼、 in [3]with different m 微笑或者严肃)以及脸部细节变化(如是否戴眼 镜),所有的照片都是正面直立的,允许一定角度的 头部倾斜和旋转,一般旋转角度不超过20°.这有利 于验证SPCA参数是否可以抑制无用干扰信息,对 n=1.1 n=1.2 n=1.3 =1.4 n=1.5 于分析参数变化对识别效果的影响是有利的 实验中选取40个人,每人一幅具有正常表情的 标准人脸图像作为训练样本库,剩余的360幅图像 1=1.6 n=1.7n=1.8n=1.9n=2.0 用于测试.图1给出了其中一个人的图像. (a)a=0.25时的衍生图像
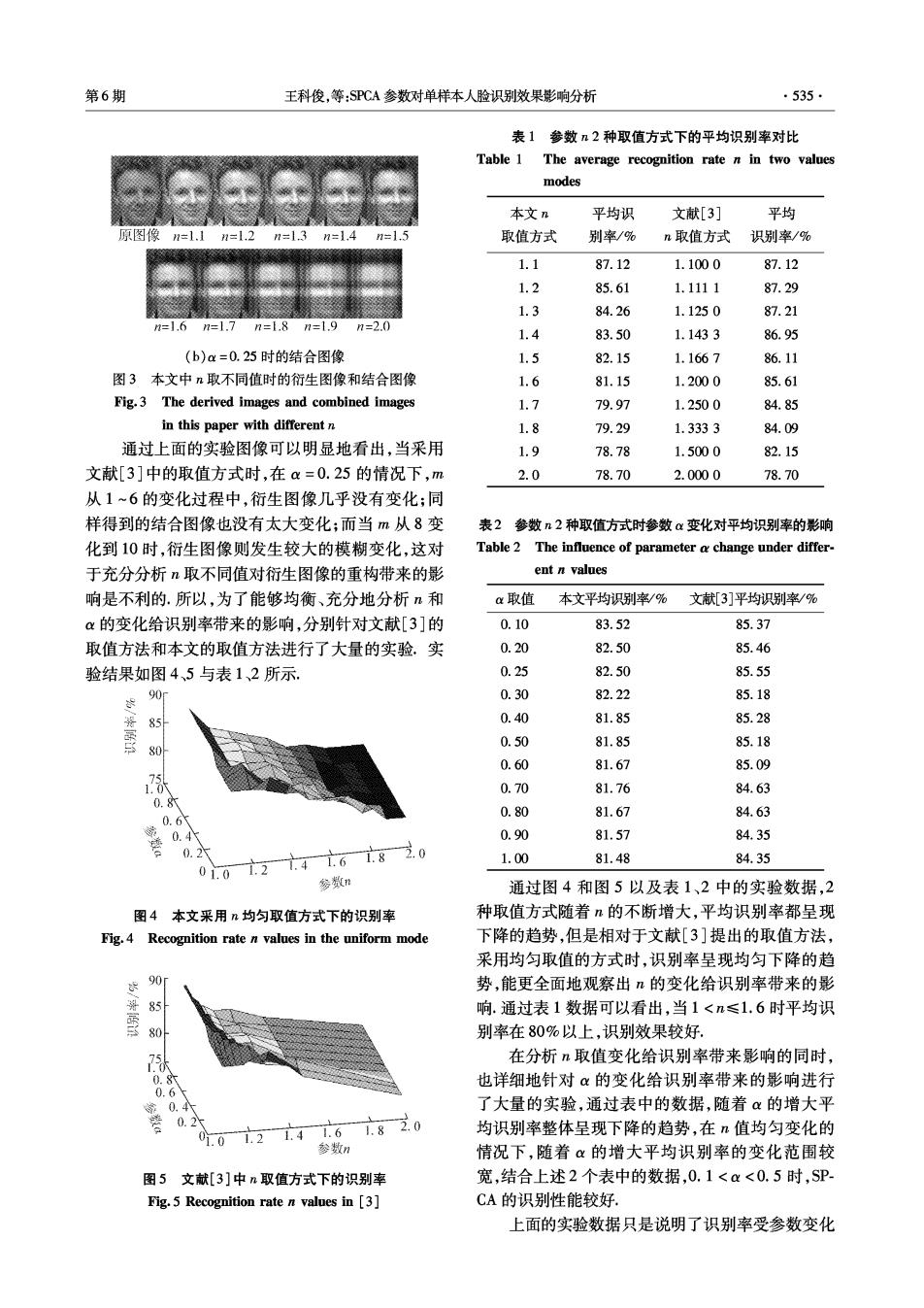
第6期 王科俊,等:SPCA参数对单样本人脸识别效果影响分析 ·535· 表1参数n2种取值方式下的平均识别率对比 Table 1 The average recognition rate n in two values modes 本文n 平均识 文献[3] 平均 原图像n=1.11=1.2n=1.3n=1.4 =1.5 取值方式 别率/% n取值方式 识别率/% 1.1 87.12 1.1000 87.12 1.2 85.61 1.1111 87.29 1.3 84.26 1.1250 87.21 1=1.6n=1.7n=1.8n=1.9n=2.0 1.4 83.50 1.1433 86.95 (b)a=0.25时的结合图像 1.5 82.15 1.1667 86.11 图3本文中n取不同值时的衍生图像和结合图像 1.6 81.15 1.2000 85.61 Fig.3 The derived images and combined images 1.7 79.97 1.2500 84.85 in this paper with different n 1.8 79.29 1.3333 84.09 通过上面的实验图像可以明显地看出,当采用 1.9 78.78 1.5000 82.15 文献[3]中的取值方式时,在a=0.25的情况下,m 2.0 78.70 2.0000 78.70 从1~6的变化过程中,衍生图像几乎没有变化:同 样得到的结合图像也没有太大变化;而当m从8变 表2 参数n2种取值方式时参数α变化对平均识别率的影响 化到10时,衍生图像则发生较大的模糊变化,这对 Table 2 The influence of parameter a change under differ- 于充分分析取不同值对衍生图像的重构带来的影 ent n values 响是不利的.所以,为了能够均衡、充分地分析和 a取值 本文平均识别率/% 文献[3]平均识别率/% α的变化给识别率带来的影响,分别针对文献[3]的 0.10 83.52 85.37 取值方法和本文的取值方法进行了大量的实验.实 0.20 82.50 85.46 验结果如图4、5与表1、2所示 0.25 82.50 85.55 90 0.30 82.22 85.18 85 0.40 81.85 85.28 0.50 81.85 85.18 80 0.60 81.67 85.09 7 0.70 81.76 84.63 0.8 0.80 81.67 84.63 0.6 0.4 0.90 81.57 84.35 0.0124i682.0 0.2六 1.00 81.48 84.35 参数n 通过图4和图5以及表1、2中的实验数据,2 图4本文采用n均匀取值方式下的识别率 种取值方式随着n的不断增大,平均识别率都呈现 Fig.4 Recognition rate n values in the uniform mode 下降的趋势,但是相对于文献[3]提出的取值方法, 采用均匀取值的方式时,识别率呈现均匀下降的趋 90i 势,能更全面地观察出n的变化给识别率带来的影 85 响.通过表1数据可以看出,当1<n≤1.6时平均识 80 别率在80%以上,识别效果较好. 7 在分析n取值变化给识别率带来影响的同时, 0.8 也详细地针对α的变化给识别率带来的影响进行 0.6 了大量的实验,通过表中的数据,随着α的增大平 0.2 0h.012i4i.6.82.0 均识别率整体呈现下降的趋势,在n值均匀变化的 参数n 情况下,随着α的增大平均识别率的变化范围较 图5文献[3]中n取值方式下的识别率 宽,结合上述2个表中的数据,0.1<<0.5时,SP Fig.5 Recognition rate n values in [3] CA的识别性能较好 上面的实验数据只是说明了识别率受参数变化