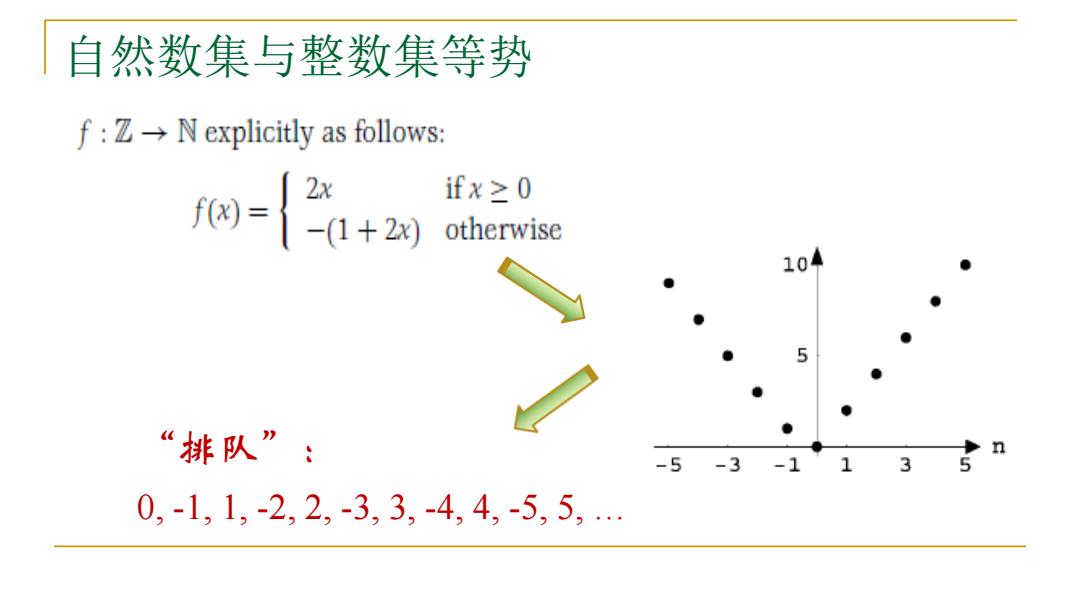
自然数集与整数集等势 f:ZN explicitly as follows: f-{+2刘 2x ifx≥0 otherwise 104 5 “排队”: -5-3 -1 0,-1,1,-2,2,-3,3,-4,4,-5,5
自然数集与整数集等势 “排队”: 0, -1, 1, -2, 2, -3, 3, -4, 4, -5, 5, …

问题5: 63,-2,-1,0,1,2,39不 能算排好队”了,为什么?

关于双射的证明(1) f:ZN explicitly as follows: 注意: 2x f=1 ifx≥0 不能遗漏了case3! -(1+2x)otherwise Proof that f is one-to-one. Letm,n∈Z and suppose that f(m)≠f(n). Case 1.Suppose that m 0 and n z0.Then f(m)=2m and f(n)=2n.Thus 2m =2n,and therefore m =n. Case 2.Suppose that m<0 and n 0.Then f(m)=-2m-1 and f(n)=-2n-1.Thus,-2m-1 =-2n-1,and therefore m n. Case 3.Suppose that one of the two,say m,is nonnegative,and the other is negative.Then f(m)=2m and f(n)=-2n-1. Thus 2m =-2n-1.But this means that an even number, 2m,is equal to an odd number,-2n-1,which is impossible. Therefore,if f(m)=f(n),only case 1 and case 2 can occur.In either of these cases,we have shown that m n.Thus f is one-to- one. ■
关于双射的证明 (1) 注意: 不能遗漏了case 3!