
效绵鼎 Labeled transition systems A transition system labeled by an alphabet 4 is a 6- tuple A=<S,So,T,a,B,a>where o<S,So,T,a,B>is a transition system, o A is a mapping from T to A taking each transition t to its label 1(t) Intuitively,the label of a transition indicates the action or event which triggers the transition
Labeled transition systems ◼ A transition system labeled by an alphabet A is a 6- tuple 𝒜 =< 𝑆, 𝑆0 ,𝑇, 𝛼, 𝛽, 𝜆 > where < 𝑆, 𝑆0 , 𝑇,𝛼,𝛽 > is a transition system, 𝜆 is a mapping from T to A taking each transition t to its label 𝜆(𝑡) ◼ Intuitively, the label of a transition indicates the action or event which triggers the transition
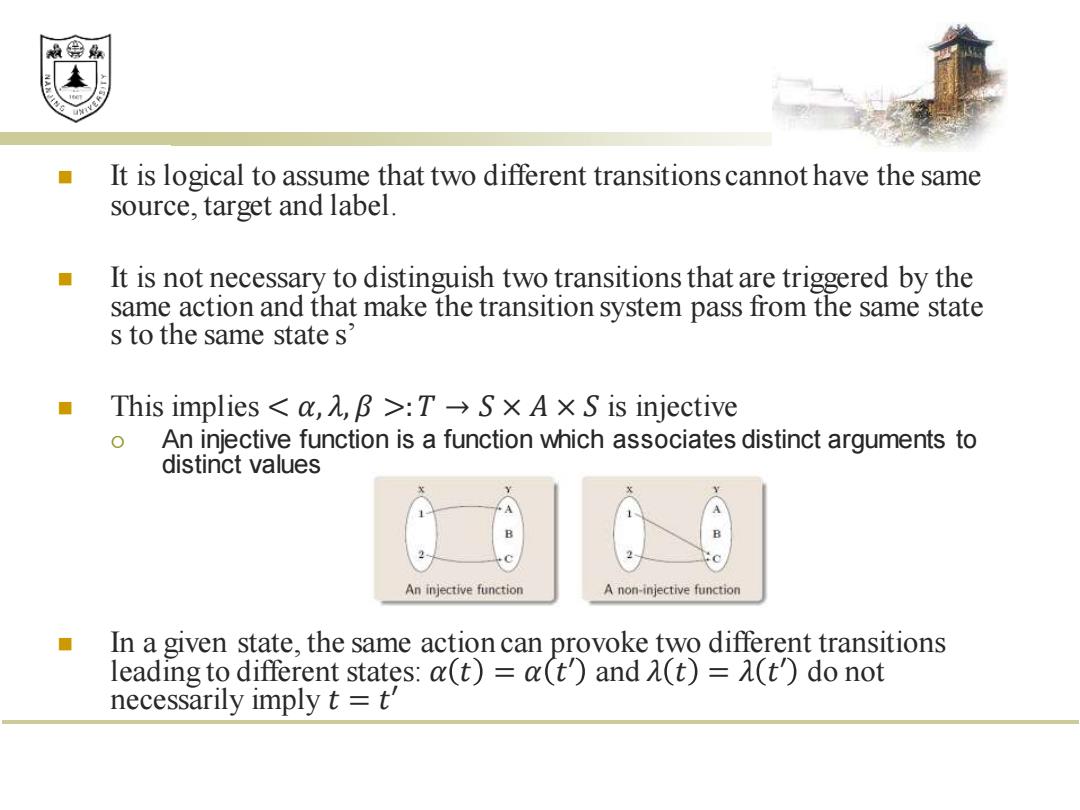
效绵县 It is logical to assume that two different transitions cannot have the same source,target and label. It is not necessary to distinguish two transitions that are triggered by the same action and that make the transition system pass from the same state s to the same state s This implies<a,l,B>:T→×A×S is injective An injective function is a function which associates distinct arguments to distinct values An injective function A non-injective function In a given state,the same action can provoke two different transitions leading to different states:a(t)=a(t)and (t)=(t)do not necessarily imply t t
◼ It is logical to assume that two different transitions cannot have the same source, target and label. ◼ It is not necessary to distinguish two transitions that are triggered by the same action and that make the transition system pass from the same state s to the same state s’ ◼ This implies < 𝛼, 𝜆, 𝛽 >:𝑇 → 𝑆 × 𝐴 × 𝑆 is injective An injective function is a function which associates distinct arguments to distinct values ◼ In a given state, the same action can provoke two different transitions leading to different states: 𝛼 𝑡 = 𝛼 𝑡′ and 𝜆 𝑡 = 𝜆 𝑡′ do not necessarily imply 𝑡 = 𝑡′
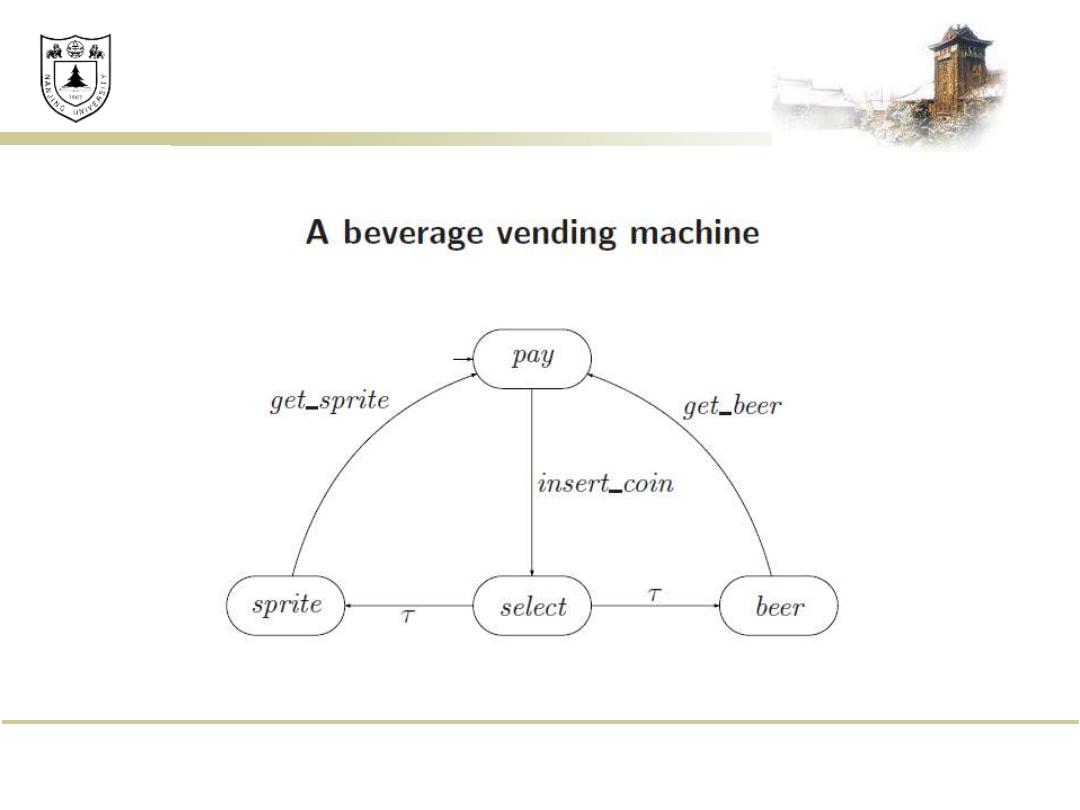
效绵鼎 A beverage vending machine pay get_sprite get_beer insert_coin sprite T select T beer

效绵鼎 Traces If c=t1,t2,is a path in a labeled transition system,the sequence of actions trace(c)=A(t), λ(t2)…is called the trace of the path
Traces ◼ If c = 𝑡1 , 𝑡2 ⋯ , is a path in a labeled transition system, the sequence of actions trace(c) = 𝜆(𝑡1 ), 𝜆(𝑡2 ) ⋯ is called the trace of the path

效绵鼎 Equivalence Relation A relation R XXX is an equivalence (relation)if and only if Reflexive:for all x∈X:(xx)∈R Symmetric:for all x,y EX:if (x,y)E R,then (y,x) ∈R ■ Transitive:for all x,y,zEX:if(x,y)E R and (y,z) ∈R then(&Z)∈R
Equivalence Relation ◼ A relation R ⊆ X × X is an equivalence (relation) if and only if ◼ Reflexive: for all x ∈ X : (x, x) ∈ R ◼ Symmetric: for all x, y ∈ X : if (x, y) ∈ R, then (y, x) ∈ R ◼ Transitive: for all x, y, z ∈ X : if (x, y) ∈ R and (y, z) ∈ R then (x, z) ∈ R