
效绵鼎 There are numerous notions of equivalency for transition systems We consider the following: o Strong isomorphism o Weak isomorphism Bisimulation equivalence Bisimulation Equivalence Weak Isomorphism Equivalence Strong Isomorphism Equivalence
◼ There are numerous notions of equivalency for transition systems ◼ We consider the following: Strong isomorphism Weak isomorphism Bisimulation equivalence

效绵鼎 Transition system homomorphism Definition:Let A=<S,So,T,a,B and A'=< S,S'o,T,a',B'>be two transition systems.A homomorphism h from A to A'is a pair (ha,h )of mappings ho:S→S hx:T→T' which satisfies,for every transition t of T: a'(h(t)=ha(a(t) B'(h(t)=hg(B(t)
Transition system homomorphism ◼ Definition:Let 𝒜= < 𝑆, 𝑆0 , 𝑇, 𝛼, 𝛽 > and 𝒜’ = < 𝑆′ , 𝑆′ 0 ,𝑇′ , 𝛼′ , 𝛽′ > be two transition systems. A homomorphism h from 𝒜 to 𝒜’ is a pair (ℎ𝜎, ℎ𝜏 )of mappings ℎ𝜎: 𝑆 → 𝑆′ ℎ𝜏 :𝑇 → 𝑇′ which satisfies, for every transition t of T: 𝛼′(ℎ𝜏 (𝑡)) = ℎ𝜎 𝛼 𝑡 , 𝛽′(ℎ𝜏 (𝑡)) = ℎ𝜎 𝛽 𝑡

效绵鼎 Labeled transition system homomorphism Let A=<S,So,T,a,B,A>and A'=< S',S'o,T,a',B',A'>be two transition systems labeled by the same alphabet.A labeled transition system homomorphism from A to A'is a homomorphism h which also satisfies the condition λ'(hz(t)=(t)
◼ Labeled transition system homomorphism ◼ Let 𝒜= < 𝑆, 𝑆0 ,𝑇, 𝛼,𝛽, 𝜆 > and 𝒜’ = < 𝑆′, 𝑆′0 ,𝑇′, 𝛼′ , 𝛽′ , 𝜆 ′ >be two transition systems labeled by the same alphabet. A labeled transition system homomorphism from 𝒜 to 𝒜’ is a homomorphism h which also satisfies the condition 𝜆′(ℎ𝜏 (𝑡)) = 𝜆(𝑡)
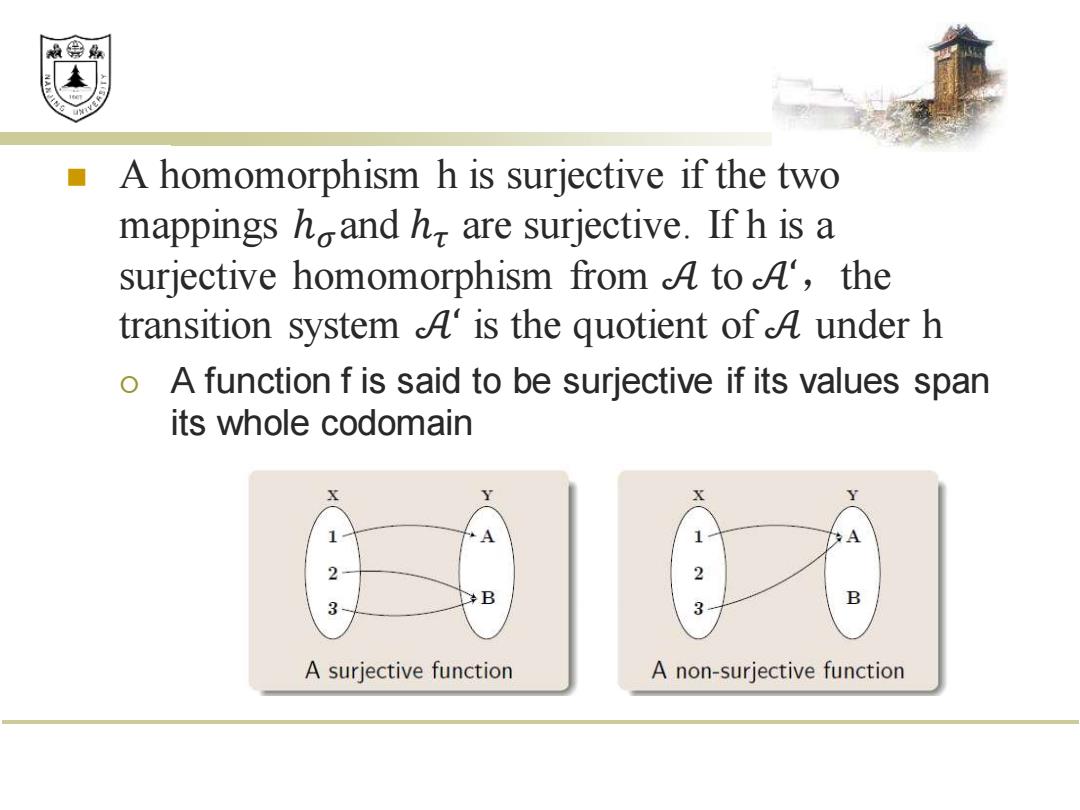
效绵鼎 A homomorphism h is surjective if the two mappings hoand h are surjective.If h is a surjective homomorphism from A to A',the transition system 4 is the quotient ofA under h 0 A function f is said to be surjective if its values span its whole codomain X X A 2 B B 3 A surjective function A non-surjective function
◼ A homomorphism h is surjective if the two mappings ℎ𝜎and ℎ𝜏 are surjective. If h is a surjective homomorphism from 𝒜 to 𝒜‘ ,the transition system 𝒜‘ is the quotient of 𝒜 under h A function f is said to be surjective if its values span its whole codomain

效绵鼎 A TS strong isomorphism is a TS homomorphism where hoand h are bijiective. In this case,the inverse mappings g=<go,g>is itself a isomorphism. If two TS are strong isomorphic,the only difference can be how they are named. o A function f is a bijective function if it is both injective and surjective.(This is often called a "one-to-one correspondence”.) Isomorphic is a kind of equivalence
◼ A TS strong isomorphism is a TS homomorphism where ℎ𝜎and ℎ𝜏are bijiective. ◼ In this case, the inverse mappings 𝑔 =< 𝑔𝜎, 𝑔𝜏 > is itself a isomorphism. ◼ If two TS are strong isomorphic, the only difference can be how they are named. A function f is a bijective function if it is both injective and surjective.(This is often called a “one-to-one correspondence”.) ◼ Isomorphic is a kind of equivalence