
9.2.1直角坐标条 ■电矢量可分解为任意两个相互垂直方向上的分量: Ex =X sin(@t-Ex) Ey=Ysin(@t-Ey) ■电矢量端点的轨迹方程: X y2-2 cosδ=sin28 XY XY:振幅;O:角频率;8xCy:初始相位角;δ=8x8y:相位角 振幅、Y和相位角δ决定了偏振的状态 用X、丫和δ可充分描述该椭圆偏振波 16
16 9.2.1 直角坐标系 n 电矢量端点的轨迹方程: d d 2 2 2 2 2 + - 2 cos = sin XY E E Y E X Ex y x y sin( ) sin( ) y y x x E Y t E X t w e w e = - = - Ex Ey n 电矢量可分解为任意两个相互垂直方向上的分量: XY:振幅;w:角频率;exey:初始相位角;d= ex- ey:相位角 振幅X、Y和相位角d决定了偏振的状态 用X、Y和d可充分描述该椭圆偏振波

E =X sin(ot-) Ey=Ysin(ot-ex+δ) ■一般情况,δ=8x8y丰mπ(m=0,±1,±士2,.…) 口电矢量E的矢端轨迹为一楠圆一椭圆偏振光 口兀<δ<0,X轴相位超前,电矢量逆时针方向运动,左旋偏振 口0<δ<π,y轴相位超,电矢量顺时针方向运动,右旋偏振 ■偏振方位角,椭圆主轴与X轴夹角ψ: Y E 2XY Ψ Ex g2w-Xycos -X O X 17
17 sin( ) sin( ) w e d w e = - + = - y x x x E Y t E X t n 一般情况,d= ex- ey ≠ mp (m=0, ±1, ±2,…) q 电矢量E的矢端轨迹为一椭圆——椭圆偏振光 q -p<d<0,x轴相位超前,电矢量逆时针方向运动,左旋偏振 q 0<d<p,y轴相位超前,电矢量顺时针方向运动,右旋偏振 n 偏振方位角,椭圆主轴与X轴夹角ψ: tg2ψ = 2XY X2 −Y 2 cosδ -X X Y -Y O Ex Ey E ψ

E =X sin(ot-, E,=Ysin(ot-&x+δ) 当8=mπ(m=0,士1,士2,.)时:×、y分量同相或反相 楠圆变为直线,线偏振波 当δ=m元,m为偶数时:X、y分量同相 一、三象限直线方程 Ey =Y.Ex/X ■ 当δ=m元,m为奇数时:X、y分量反相 二、四象限直线方程 Ey=-Y.Ex/X ■ 当δ=(2m+1)/2(m=0,±1,±2,…)时:相位相差90度 标准楠圆方程,主轴与坐标轴重合 Ex2/x2+Ey2/Y2=1 ■δ=(2m+1)/2(m=0,±1,±2,…),且X=Y时: 则电矢量E的矢端轨迹为圆一圆偏振光 Ex2+Ey2-Y2 18
18 n 当d=mp (m=0, ±1, ±2,…)时:x、y分量同相或反相 椭圆变为直线,线偏振波 n 当d=mp,m 为偶数时:x、y分量同相 一、三象限直线方程 n 当d=mp ,m 为奇数时:x、y分量反相 二、四象限直线方程 n 当d=(2m+1)p/2 (m=0, ±1, ±2,…)时:相位相差90度 标准椭圆方程,主轴与坐标轴重合 n d=(2m+1)p/2 (m=0, ±1, ±2,…),且X=Y时: 则电矢量E的矢端轨迹为圆—圆偏振光 Ey = Y×Ex X E X E Y 1 2 2 y 2 2 x + = 2 2 y 2 Ex +E = Y Ey = - Y×Ex X = sin(w -e ) = sin(w -e +d ) x x y x E X t E Y t
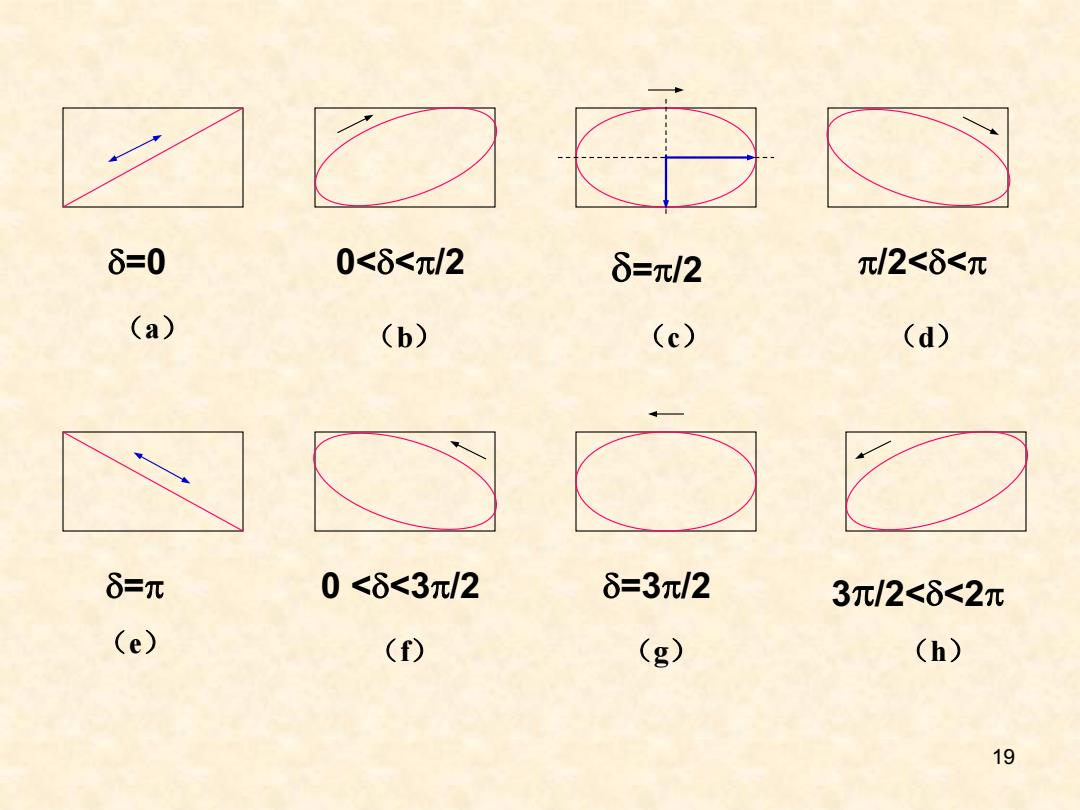
8=0 0<δ<π/2 δ=元/2 π/2<δ<元 (a) (b) (c) (d) 8=元 0<δ<3π/2 δ=3π/2 3元/2<6<2元 (e) (f) (g) (h) 19
19 (a) d=0 (b) 0<d<p/2 (d) p/2<d<p (e) d=p (f) 0 <d<3p/2 (g) d=3p/2 (h) 3p/2<d<2p (c) d=p/2

9.2.2斯托克斯参数 ■简单波的偏振态,可以用振幅X 、Y和相位角δ描述 英国物理学家 斯托克斯 ■但是振幅和相位角的量纲彼此 不同 ■用来讨论偏振辐射经过介质后偏 振状态发生的变化时,非常不方 便,有时甚至复杂的无法解决! ■1852年,斯托克斯发现辐射偏 振可以用实验观测量来描述 20
20 n 简单波的偏振态,可以用振幅X 、Y和相位角d描述 n 但是振幅和相位角的量纲彼此 不同 n 用来讨论偏振辐射经过介质后偏 振状态发生的变化时,非常不方 便,有时甚至复杂的无法解决! n 1852年,斯托克斯发现辐射偏 振可以用实验观测量来描述 英国物理学家 斯托克斯 9.2.2 斯托克斯参数