
Maximum Likelihood vs.Bayesian Maximum likelihood estimation -"Best"means "data likelihood reaches maximum" 6=arg max P(X1) Problem:small sample 。Bayesian estimation -"Best"means being consistent with our "prior" knowledge and explaining data well G=arg max P(X)=arg max P(X1)P() Problem:how to define prior? CCF-ADL at Zhengzhou University, June25-27,2010
CCF-ADL at Zhengzhou University, June 25-27, 2010 12 Maximum Likelihood vs. Bayesian • Maximum likelihood estimation – “Best” means “data likelihood reaches maximum” – Problem: small sample • Bayesian estimation – “Best” means being consistent with our “prior” knowledge and explaining data well – Problem: how to define prior? arg max ( | ) ˆ = P X arg max ( | ) arg max ( | ) ( ) ˆ = P X = P X P
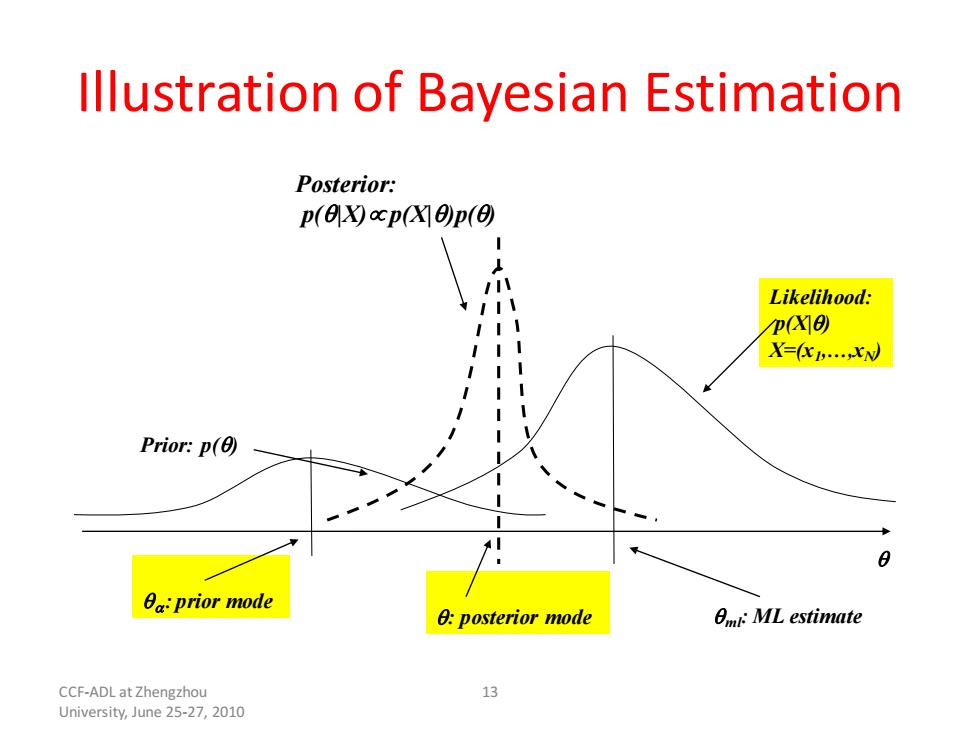
Illustration of Bayesian Estimation Posterior: p(Oycp凶a)p© Likelihood: P(XO X=(化心 Prior:p() 0a:prior mode 0:posterior mode Om:ML estimate CCF-ADL at Zhengzhou 13 University,June 25-27,2010
CCF-ADL at Zhengzhou University, June 25-27, 2010 13 Illustration of Bayesian Estimation Prior: p() Likelihood: p(X|) X=(x1 ,…,xN) Posterior: p(|X) p(X|)p() : prior mode ml : posterior mode : ML estimate

Maximum Likelihood Estimate Data:a documentd with counts c(w),...,c(w),and length ldl Model:multinomial distribution M with parameters (p(wi)} Likelihood:p(dM) Maximum likelihood estimator:M-argmax M p(dM) dn-(lJenem where,.&=pw) I(dM)=log p(dM)c()og0 We'll tune p(wi)to maximize I(dM) 1dn-立4wlag8+a空g-y Use Lagrange multiplier approach -cw)+=0→日=-e01 Set partial derivatives to zero a0, Since) c(or)=-ldl So.a=pom )2t ML estimate CCF-ADL at Zhengzhou University, 14 June25-27,2010
CCF-ADL at Zhengzhou University, June 25-27, 2010 14 Maximum Likelihood Estimate Data: a document d with counts c(w1 ), …, c(wN), and length |d| Model: multinomial distribution M with parameters {p(wi )} Likelihood: p(d|M) Maximum likelihood estimator: M=argmax M p(d|M) ( ) ( ) 1 1 1 1 ' 1 1 ' 1 1 | | ( | ) , ( ) ( )... ( ) ( | ) log ( | ) ( )log ( | ) ( )log ( 1) ( ) ( ) 0 1, ( ) | | i i N N c w c w i i i i N i i N i i i N N i i i i i i i i i i N N i i i i d p d M where p w c w c w l d M p d M c w l d M c w l c w c w Since c w d So = = = = = = = = = = = = + − = + = = − = = − = − ( ) , ( ) | | i i i c w p w d = = We’ll tune p(wi ) to maximize l(d|M) Use Lagrange multiplier approach Set partial derivatives to zero ML estimate 1 1 = = N i i

What You Should Know Probability concepts: sample space,event,random variable,conditional prob.multinomial distribution,etc Bayes formula and its interpretation · Statistics:Know how to compute maximum likelihood estimate CCF-ADL at Zhengzhou University, 15 June25-27,2010
CCF-ADL at Zhengzhou University, June 25-27, 2010 15 What You Should Know • Probability concepts: – sample space, event, random variable, conditional prob. multinomial distribution, etc • Bayes formula and its interpretation • Statistics: Know how to compute maximum likelihood estimate

Essential Background 2: Basic Concepts in Information Theory
Essential Background 2: Basic Concepts in Information Theory