
弯曲表面下的附加压力 1在平面上 研究以AB为直径的一个环作 为边界,由于环上每点的两边都 存在表面张力,大小相等,方向 相反,所以没有附加压力。 剖面图 设向下的大气压力为P。, 向上的反作用力也为P。,附加 压力P等于零。 Ps=P。-P。=0 液面正面图 4上一内容 下一内容 ◇回主目录 与返回 2024/9/19
上一内容 下一内容 回主目录 返回 2024/9/19 弯曲表面下的附加压力 1.在平面上 剖面图 液面正面图 研究以AB为直径的一个环作 为边界,由于环上每点的两边都 存在表面张力,大小相等,方向 相反,所以没有附加压力。 设向下的大气压力为Po, 向上的反作用力也为Po ,附加 压力Ps等于零。 Ps = Po - Po =0

弯曲表面下的附加压力 (2) 在凸面上: 研究以AB为弦长的一个球面 上的环作为边界。由于环上每点 两边的表面张力都与液面相切, Hg 剖面图 大小相等,但不在同一平面上, 所以会产生一个向下的合力。 所有的点产生的总压力为 Ps,称为附加压力。凸面上受 的总压力为:Po+Ps P。为大气压力,P为附加压力。 附加压力示意图 上一内容 下一内容 ◇回主目录 与返回 2024/9/19
上一内容 下一内容 回主目录 返回 2024/9/19 弯曲表面下的附加压力 (2)在凸面上: 剖 面 图 附加压力示意图 研究以AB为弦长的一个球面 上的环作为边界。由于环上每点 两边的表面张力都与液面相切, 大小相等,但不在同一平面上, 所以会产生一个向下的合力。 所有的点产生的总压力为 Ps ,称为附加压力。凸面上受 的总压力为: Po+ Ps Po为大气压力, Ps为附加压力
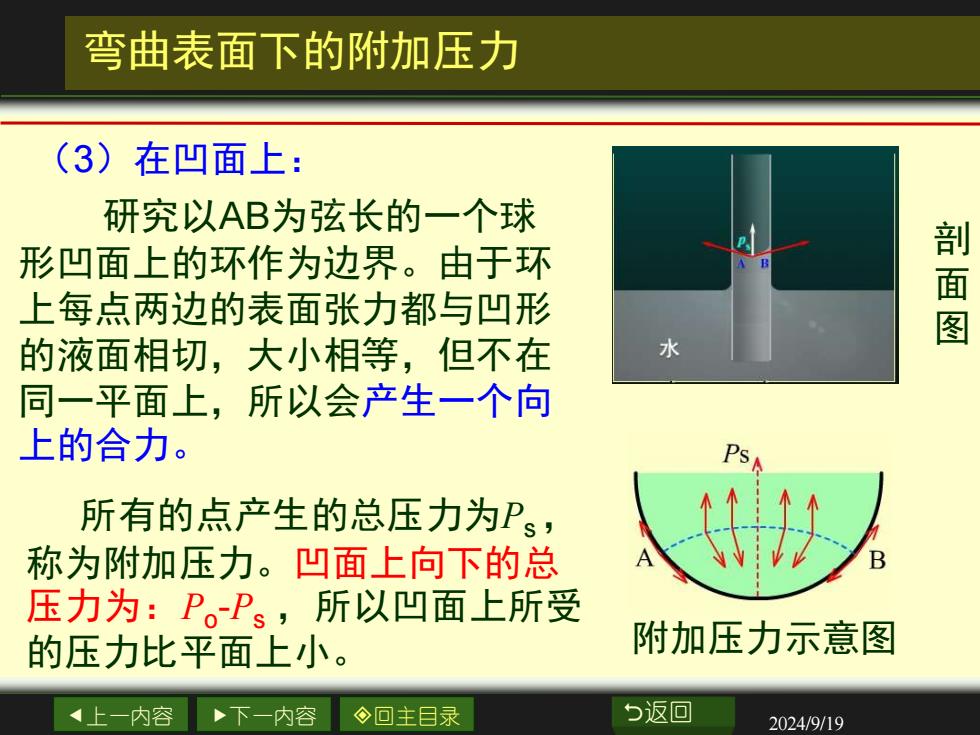
弯曲表面下的附加压力 (3)在凹面上: 研究以AB为弦长的一个球 形凹面上的环作为边界。由于环 上每点两边的表面张力都与凹形 剖面图 的液面相切,大小相等,但不在 水 同一平面上,所以会产生一个向 上的合力。 所有的点产生的总压力为Ps, 称为附加压力。凹面上向下的总 压力为:P。Ps,所以凹面上所受 的压力比平面上小。 附加压力示意图 4上一内容 下一内容 ◇回主目录 b返回 2024/9/19
上一内容 下一内容 回主目录 返回 2024/9/19 弯曲表面下的附加压力 (3)在凹面上: 剖 面 图 附加压力示意图 研究以AB为弦长的一个球 形凹面上的环作为边界。由于环 上每点两边的表面张力都与凹形 的液面相切,大小相等,但不在 同一平面上,所以会产生一个向 上的合力。 所有的点产生的总压力为Ps , 称为附加压力。凹面上向下的总 压力为:Po -Ps ,所以凹面上所受 的压力比平面上小

杨-拉普拉斯公式 1805年Young-Laplace导出了附加压力与曲率半 径之间的关系式: 一般式: P-o(R R 特殊式(对球面): R 根据数学上规定,凸面的曲率半径取正值,凹 面的曲率半径取负值。所以,凸面的附加压力指向 液体,凹面的附加压力指向气体,即附加压力总是 指向球面的球心。 上一内容 下一内容 ◇回主目录 5返回 2024/9/19
上一内容 下一内容 回主目录 返回 2024/9/19 杨-拉普拉斯公式 1805年Young-Laplace导出了附加压力与曲率半 径之间的关系式: 特殊式(对球面): s ' 2 P R = 根据数学上规定,凸面的曲率半径取正值,凹 面的曲率半径取负值。所以,凸面的附加压力指向 液体,凹面的附加压力指向气体,即附加压力总是 指向球面的球心。 一般式: s ' ' 1 2 1 1 P ( ) R R = +

Young-Laplace特殊式的推导 (1)在毛细管内充满液体, 管端有半径为R'的球状液 滴与之平衡。 外压为p0,附加压力 o 为△p,液滴所受总压为: Po+△p 4上一内容 下一内容 ◇回主目录 与返回 2024/9/19
上一内容 下一内容 回主目录 返回 2024/9/19 Young-Laplace特殊式的推导 (1)在毛细管内充满液体, 管端有半径为R’ 的球状液 滴与之平衡。 外压为 p0 ,附加压力 为 Δp ,液滴所受总压为: p0 + Δp