
结论:S第画1.凡是由偶点组成的连通图,一定可以一笔画成画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图o2.凡是只有两个奇点的连通图(其余都为偶点),一料!定可以一笔画成画时必须把一个奇点为起点,另一个奇点终点。3.其他情况的图都不能一笔画出。(奇点数除以二便可算出此图需几笔画成。外传!
SDUT 内 部 资 料! 请 勿 外 传! 结论:一笔画 ⒈凡是由偶点组成的连通图,一定可以一笔画成; 画时可以把任一偶点为起点,最后一定能以这个点为终 点画完此图。 ⒉凡是只有两个奇点的连通图(其余都为偶点),一 定可以一笔画成; 画时必须把一个奇点为起点,另一个奇点终点。 ⒊其他情况的图都不能一笔画出。 (奇点数除以二便可算出此图需几笔画成
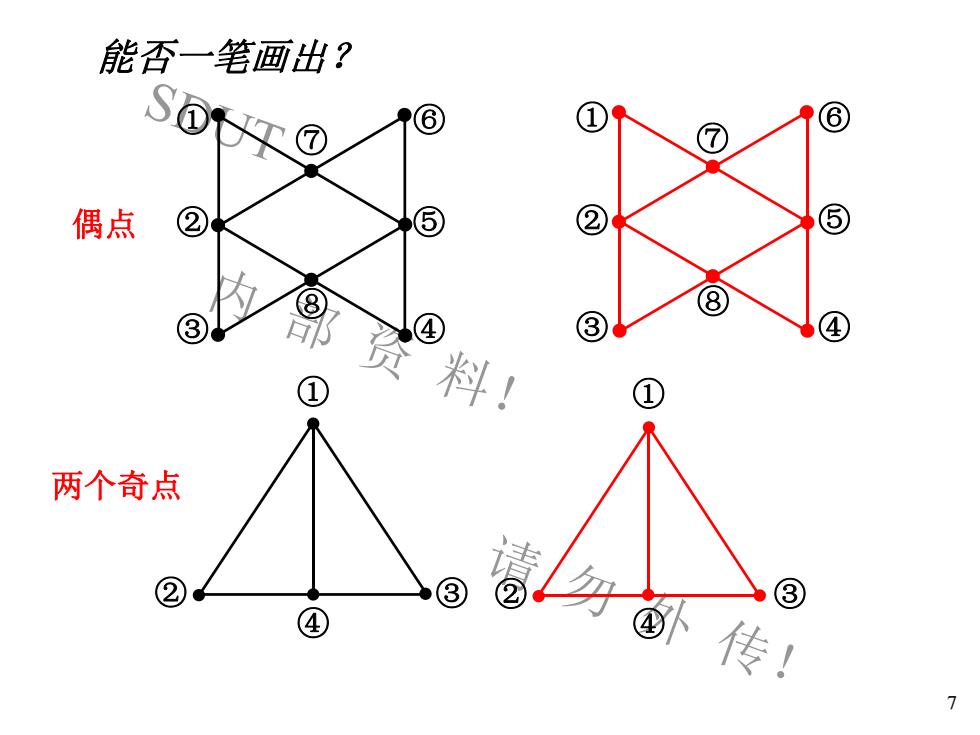
能否一笔画出?SD偶点53资料两个奇点?X传
SDUT 内 部 资 料! 请 勿 外 传! 7 ① ② ③ ④ ① ② ③ ④ ② ① ⑥ ⑤ ③ ④ ⑦ ① ② ③ ⑦ ④ ⑤ ⑥ ⑧ ⑧ 能否一笔画出? 两个奇点 偶点

奥运会的五环标志能否一笔画出?内部落*图论是拓扑学(Topology)的一个分支,是富有趣味和应用极为广泛的一门学科。图论的概念由瑞士数学家欧拉最早提出(最早的记载是1736年)。1847年,基尔霍夫首先用图论来分析电网络,如今在电工领域,图论被用于网络分析与综合、通讯网络与开关网络的设计、集成电路布局及故障诊断、计算机结构设计及编译技采等等。8
SDUT 内 部 资 料! 请 勿 外 传! 8 奥运会的五 环标志能否 一笔画出? 图论是拓扑学(Topology)的一个分支,是富有趣味和应 用极为广泛的一门学科。图论的概念由瑞士数学家欧拉最 早提出 (最早的记载是1736年)。 1847年,基尔霍夫首先 用图论来分析电网络,如今在电工领域,图论被用于网络 分析与综合、通讯网络与开关网络的设计、集成电路布局 及故障诊断、计算机结构设计及编译技术等等
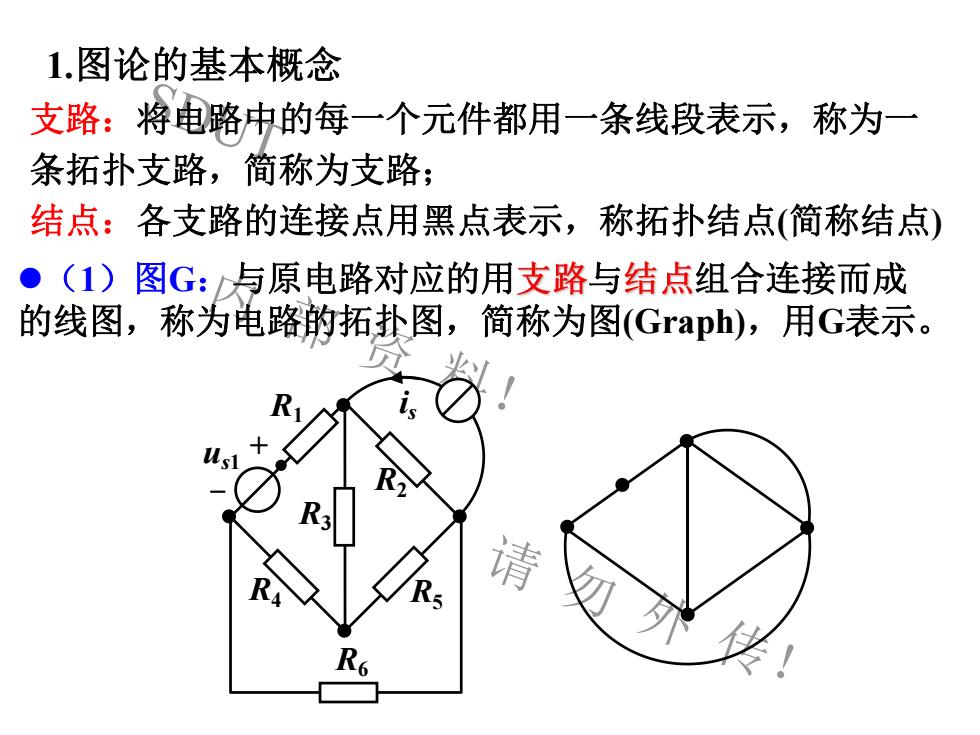
1.图论的基本概念支路:将电路中的每一个元件都用一条线段表示,称为一条拓扑支路,简称为支路:结点:各支路的连接点用黑点表示,称拓扑结点(简称结点)(1)图G:与原电路对应的用支路与结点组合连接而成的线图,称为电路的拓扑图,简称为图(Graph),用G表示isRR2R3请R5R6
SDUT 内 部 资 料! 请 勿 外 传! l(1)图G:与原电路对应的用 与 组合连接而成 的线图,称为电路的拓扑图,简称为图(Graph),用G表示。 1.图论的基本概念 R1 R2 u + s1 is R3 R4 R5 R6 - 支路:将电路中的每一个元件都用一条线段表示,称为一 条拓扑支路,简称为支路; 结点:各支路的连接点用黑点表示,称拓扑结点(简称结点)
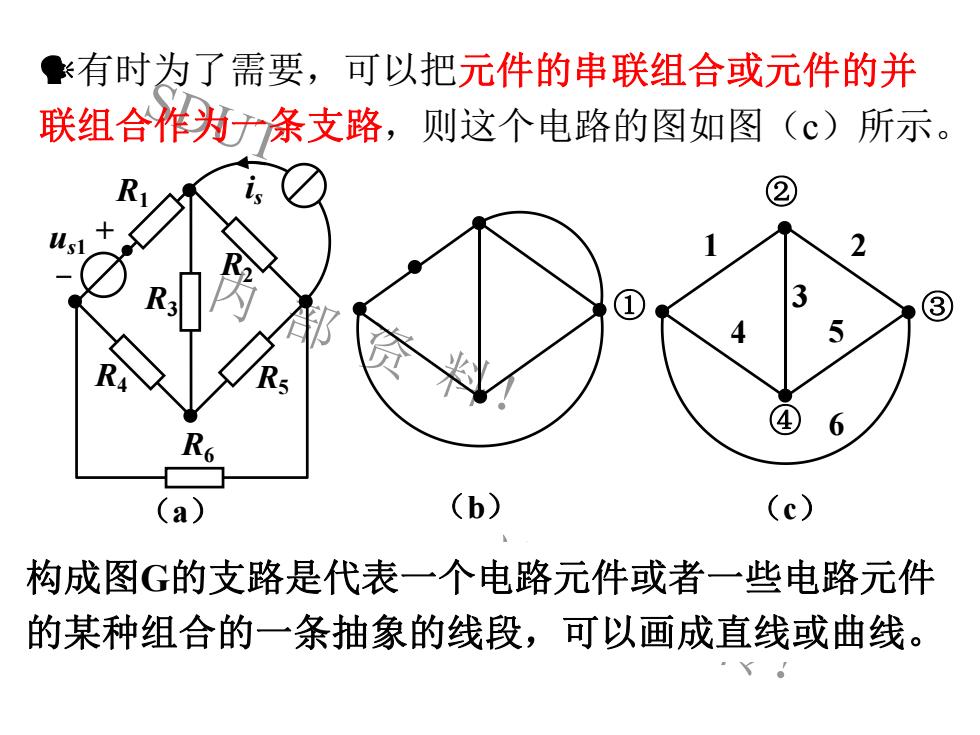
有时为了需要,可以把元件的串联组合或元件的并联组合作为干条支路,则这个电路的图如图(c)所示R22Us3R1354R56R6(b)()(a)构成图G的支路是代表一个电路元件或者一些电路元件的某种组合的一条抽象的线段,可以画成直线或曲线
SDUT 内 部 资 料! 请 勿 外 传! 有时为了需要,可以把元件的串联组合或元件的并 联组合作为一条支路,则这个电路的图如图(c)所示。 ② 1 2 4 5 6 ① ③ ④ 3 (c) 构成图G的支路是代表一个电路元件或者一些电路元件 的某种组合的一条抽象的线段,可以画成直线或曲线。 (a) R1 R2 u + s1 is R3 R4 R5 R6 - (b)