
物理化学教案 新疆大学化学化工学院物理化学教研室 刘月娥 第一章气体 聚集状态一物质的聚集状态通常有气、固、液三种状态。在研究放电管中电离气体 的性质时,发现了一表 新的导电流体, (包括带正负电荷的离子、电子以及少量未经电离的 分子、原子等,整体呈电中性,故称为等离子体。 被称为物质的第四态。另外有人把超高 压、超高温下的状态称为第五态。此外还有超导态、超流态等等。 历史上人们对气态物质的性质研究的比较多,获得了许多经验定律,然后对气体分子 的运动设计微观运动模型,从理论的角度深入研究气体分子运动的规律一一即从宏观到微 观并利用徽观图像使宏观现象得到解释 1.1气体分子动理论 对于气体在低压及较高温度下的行为,在历史上曾经归钠出一些经验定律:波义尔 (R.Bolye,.1662)定律,盖吕萨克(U.Ga-Lussac,1808)定律等。从这些经验定律可以导出低 压下气体的P、V、T之间的关系式p=mRT。 这种群系压力 、体积和温度 者间的关系式称为状态方程式。我们把在任何压力任何温 度下都能严格遵从pV=RT的气体叫做理想气体。此式又叫做理想气体的状态方程式 理想气体实际上是一个科学的抽象概念,客魂上并不存在,它只能看作是实际气体在压 力很低时的一种极限状况。 ,气体分子动理论的基太公式 为进 步说 为什么理想气体的P、V、T之间会具有Ψ nRT这样简单的关系,人们 根据对宏观现象的认识,提出了分子运动的微观模型,然后根据所设想的运动棋型来推导 运动的规律。如果据此所推出的结论与实验事实相符,则说明所设想的模型是合理正确的,经 反复考验缘正后即可上升为理论。 1、气体 分子运动的微观模型动理论P10-11 量分 子的集合体 ,相对于分子与分子间的距离以及整个容器的体积来说,气 体分子本身的体积是很小的,可以忽略不计,因此常可以将气体分子当作质点来处理。 (2)气体分子不断地作无规则的运动,均匀分布在整个容器之中 (3)分子彼此的碰靠以及分子与器壁的碰撞是完全弹性的(即在碰章前后总动量不损失)。 2、气体分子动理论的基本方程式 根据气体分子动理论微观模型)所导出的基本方程式 PV=l/3mNμ 推导过程P) 式中P是N个分子与器壁碰撞后所产生的总效应,它具有统计平均的意义 式中根均方速率μ,也是一个徽观量的统计平均值,它不能由实验直接测量, 而P和V则是可以直接由实验量度的宏观量。 因此式PV=1/3mNu2 是联系宏观可测量与微观不可测量之间的桥梁 二、压力和温度的统计概念 1、压力的统计平均意义(压力定义见P)
1 物 理 化 学 教 案 新疆大学化学化工学院物理化学教研室 刘月娥 第一章 气体 聚集状态-物质的聚集状态通常有气、固、液三种状态。在研究放电管中电离气体 的性质时,发现了一种新的导电流体,(包括带正负电荷的离子、电子以及少量未经电离的 分子、原子等,整体呈电中性,故称为等离子体。 )被称为物质的第四态。另外有人把超高 压、超高温下的状态称为第五态。此外还有超导态、超流态等等。 历史上人们对气态物质的性质研究的比较多,获得了许多经验定律,然后对气体分子 的运动设计微观运动模型,从理论的角度深入研究气体分子运动的规律-即从宏观到微 观并利用微观图像使宏观现象得到解释 1.1 气体分子动理论 对于气体在低压及较高温度下的行为,在历史上曾经归纳出一些经验定律:波义尔 (R.Bolye, 1662)定律,盖·吕萨克(J. Gay-Lussac, 1808)定律等。从这些经验定律可以导出低 压下气体的 P、V、T 之间的关系式 pV = nRT。 这种联系压力、体积和温度三者间的关系式称为状态方程式。我们把在任何压力任何温 度下都能严格遵从 pV = nRT 的气体叫做理想气体。此式又叫做理想气体的状态方程式。 理想气体实际上是一个科学的抽象概念,客观上并不存在,它只能看作是实际气体在压 力很低时的一种极限状况。 一. 气体分子动理论的基本公式 为进一步说明为什么理想气体的 P、V、T 之间会具有 pV = nRT 这样简单的关系,人们 根据对宏观现象的认识,提出了分子运动的微观模型,然后根据所设想的运动模型来推导 运动的规律。如果据此所推出的结论与实验事实相符,则说明所设想的模型是合理正确的,经 反复考验修正后,即可上升为理论。 1、气体分子运动的微观模型(动理论)P10-11 (1)气体是大量分子的集合体。相对于分子与分子间的距离以及整个容器的体积来说,气 体分子本身的体积是很小的,可以忽略不计,因此常可以将气体分子当作质点来处理。 (2)气体分子不断地作无规则的运动,均匀分布在整个容器之中 (3)分子彼此的碰撞以及分子与器壁的碰撞是完全弹性的(即在碰撞前后总动量不损失)。 2、气体分子动理论的基本方程式 根据气体分子动理论(微观模型)所导出的基本方程式 PV=1/3mNμ2 (推导过程 P11-14) 式中 P 是 N 个分子与器壁碰撞后所产生的总效应,它具有统计平均的意义。 式中根均方速率μ,也是一个微观量的统计平均值,它不能由实验直接测量。 而 P 和 V 则是可以直接由实验量度的宏观量。 因此式 PV=1/3mNμ2 是联系宏观可测量与微观不可测量之间的桥梁。 二、压力和温度的统计概念 1、压力的统计平均意义(压力定义见 P12)

()对于气体中的某一个分子来说,它与器壁的碰撞是不连续的,而且它的速度也因分子间 的互相碰撞而不断地变化,所以个别分子与器壁碰撞时,在单位时间、单位体积上所引起 的动量变化是起代不定,但由于气体是大量分子的集合, 尽管个别分子的动量变化起伏不 定,但是平均压力却是一个定位,并且是一个宏观可测的物理量。 (2)根均方速率“,是一个统计平均数值,它与各个分子的速率有关,但又不等于任何单个 分子的速率。所以压力是大量分子集合所产生的总效应。 2、温度的统 含藏 子的平 平动能®=12mμ2和温度具有平行的关系,温度越高则分子的平均动能 就越大,可写成 1/2m42-fm 温度与大量分子的平均平动能具有函数的关系,所以温度也具有宏观的统计概念。 三、气体分子运动公式对几个经验定律的说明 如 气体分子动理论所提出的关于分子运动的模型以及由此而导出的气体分子运动公 式是对的,则能够对一些经验规律给以说明。 1、Boyle-Marriote定律 将PV=13mNu2写作PV=12mu2,N,2/3对于一定量的气体,在定温下,N和12mu2 均为定值。所以上式可写作PV=C。 即定温下 定量的气 体,其体积与压力成反比 ,这个定律最初是在低压下由实验所总结出来的经验规律 。(结论 与实验事实相符) 2、Charles-GaV-Lussac定律 温度越高分子的平动能越大12mμ2=fT 低压下实验表明 P具有线性关系,根据分子动理论PV=13mN?故而可得分子的平 动能与t也具有线性关系 。设温度在0C和t时平均平动能分别是E和配 则E=Bw(l+at) 根据气体分子动理论的公式,在0C和t时, ,= 馆 2 Vo-3p -3p NEa 则y,=%1+a) 式中a就是体膨胀系数。令T=t+1/a则Vt=V0Ta=CT 即对定量的气体,在定压下,体积和T成正比,这就是Charles-Gay-Lussac定律。 3 Avogadro定律 任意两种气体当温度相同时,具有相等的平均平动能1/2mu?-12mμ: 从分子运动公式 p=Nm=子m)
2 (1)对于气体中的某一个分子来说,它与器壁的碰撞是不连续的,而且它的速度也因分子间 的互相碰撞而不断地变化,所以个别分子与器壁碰撞时,在单位时间、单位体积上所引起 的动量变化是起伏不定。但由于气体是大量分子的集合,尽管个别分子的动量变化起伏不 定,但是平均压力却是一个定值,并且是一个宏观可测的物理量。 (2)根均方速率μ,是一个统计平均数值,它与各个分子的速率有关,但又不等于任何单个 分子的速率。所以压力是大量分子集合所产生的总效应。 2、温度的统计含意 由于分子的平均平动能(Ēt=1/2 mμ2 )和温度具有平行的关系,温度越高则分子的平均动能 就越大,可写成: 1/2 mμ2 =ƒ(T) 温度与大量分子的平均平动能具有函数的关系,所以温度也具有宏观的统计概念。 三、气体分子运动公式对几个经验定律的说明 如果气体分子动理论所提出的关于分子运动的模型以及由此而导出的气体分子运动公 式是对的,则能够对一些经验规律给以说明。 1、Boyle-Marriote 定律 将 PV=1/3mNμ2 写作 PV=1/2mμ2 •N•2/3 对于一定量的气体,在定温下,N 和 1/2mμ2 均为定值。所以上式可写作 PV=C。 这就是 Boyle-Marriote 定律。 即定温下一定量的气 体,其体积与压力成反比。这个定律最初是在低压下由实验所总结出来的经验规律。(结论 与实验事实相符) 2、Charles-Gay-Lussac 定律 温度越高分子的平动能越大Ēt=1/2 mμ2 = ƒ(T) 低压下实验表明 PV-t 具有线性关系,根据分子动理论 PV=1/3mNμ2故而可得分子的平 动能与 t 也具有线性关系。设温度在 0 0C 和 t 时平均平动能分别是Ēt0 和Ētt 则 Ētt=Ēt0(1+at) 根据气体分子动理论的公式,在 0 0C 和 t 时, 式中α就是体膨胀系数。令 T=t+1/α 则 Vt=V0Tα=C’T 即对定量的气体,在定压下,体积和 T 成正比,这就是 Charles-Gay-Lussac 定律。 3、Avogadro 定律 任意两种气体当温度相同时,具有相等的平均平动能 1/2 m1μ1 2 =1/2 m2μ2 2 从分子运动公式 2 , 1 2 3 3 V Nm NE t t t t p p = = 2 0 0 ,0 1 2 3 3 V Nm NEt p p = = 0 (1 ) 则V V t t = + 2 2 1 1 1 1 1 1 1 1 1 2 1( ) 3 3 2 p V N m N m = =

p=Nm店=N,(m) 因此在同温、同压下,同体积的气体应有NN: 即同温同压下,同体积的各种气体所含有的分子个数相同,这就是Avogadro定律 4、理想气体的状态方程式 由气体分子的运动模型导出了上面三个定律,则合并后就可等到理翘气体的状态方程式。 PV=nRT. V=f(P,T,N) 假r-微 对于一定量的气体,N为常数,dN0,所以, -()(r 根据Boyle-Marriote定律, r- )日 根据Charles-Gay-Lussac定律, V=CT c-号 代入上式后得 aw=-5r+号n av 上式积分得 lnV+Hnp=nT+常数 若所取气体的量是1mol,则体积写作Vm,常数写作R,即得PV=RT 上式两边同乘以物质的量,则得 PV-nRT 5、Dalton分压定律 若在定温下,把几种不同的气体混合于容积为V的容器中,各种分子的数目分别为N,2, .,总分子数为N+八2+=N。混合气体可设想是通过如下的混合过程来完成
3 因此在同温、同压下,同体积的气体应有 N1=N2 即同温同压下,同体积的各种气体所含有的分子个数相同,这就是 Avogadro 定律 4、理想气体的状态方程式 由气体分子的运动模型导出了上面三个定律,则合并后就可等到理想气体的状态方程式, PV=nRT。 V=ƒ(p,T,N) 对于一定量的气体,N 为常数,dN=0,所以, 根据 Boyle-Marriote 定律, 根据 Charles-Gay-Lussac 定律, 代入上式后得 上式积分得 lnV+lnp=lnT+常数 若所取气体的量是 1mol,则体积写作 Vm,常数写作 R,即得 PVm=RT 上式两边同乘以物质的量 n,则得 PV=nRT 5、Dalton 分压定律 若在定温下,把几种不同的气体混合于容积为 V 的容器中,各种分子的数目分别为 N1,N2, ••••••,总分子数为 N1+ N2+ •••=N。混合气体可设想是通过如下的混合过程来完成。 2 2 2 2 2 2 2 2 2 2 1 2 1( ) 3 3 2 p V N m N m = = T N P N T P , , , V V V dV dP dT dN P T N = + + T N P N , , V V dV dP dT P T = + C V P = 2 T N, V C V P P P = − = − ' V C T = ' P N, V V C T T = = V V dV dP dT P T = − + dV dP dT V P T = − +

T,V T,V 十。→ T,V,p=? Ni,pi N2,P2 N1+W2+. 混合前 混合后 混合前, B证Nm片=E 3V 1 2N2E2 B3N,m6=37 诸式相加 ∑R=NE+NE+时 混合后 P= 3V 由于相同温度下,各气体分子具有相同的平均动能,即 E1=E2=.=E Nmx=W1+N2+. 所以 P=P+P+. 这就是Dalton分压定律(Dalton's law of partial pressure)): 即混合气体的总压等于各气体分压之和。 所谓分压,就是在同一温度下,各别气体单独存在、并占有与混合气体相同体积时所具有 的压力。 若任一种气体的分压除以总压,则得 P [2.NE 3*V N -=X 3x V 式中xi是摩尔分数。这是Dalton分压定律的另一种形式
4 诸式相加 混合后 由于相同温度下,各气体分子具有相同的平均动能,即 而 所以 这就是 Dalton 分压定律(Dalton’s law of partial pressure): 即混合气体的总压等于各气体分压之和。 所谓分压,就是在同一温度下,各别气体单独存在、并占有与混合气体相同体积时所具有 的压力。 若任一种气体的分压除以总压,则得 式中 xi 是摩尔分数。这是 Dalton 分压定律的另一种形式。 混合前 混合后 T, V N1, p1 T, V N2, p2 T, V ,p=? N1 +N2 + ••• + 混合前, + ••• 2 1 1 1 1 1 1 1 2 3 3 N p N m E V V = = 2 2 2 2 2 2 2 1 2 3 3 N p N m E V V = = 1 2 1 2 2 [ ] 3 i i P N E N E V = + + 2 3 P N E mix mix V = E E E 1 2 = = = mix N N N mix = + + 1 2 P P P = + + 1 2 2 3 2 3 i i i i i mix mix mix N E P N V x P N N E V = = =
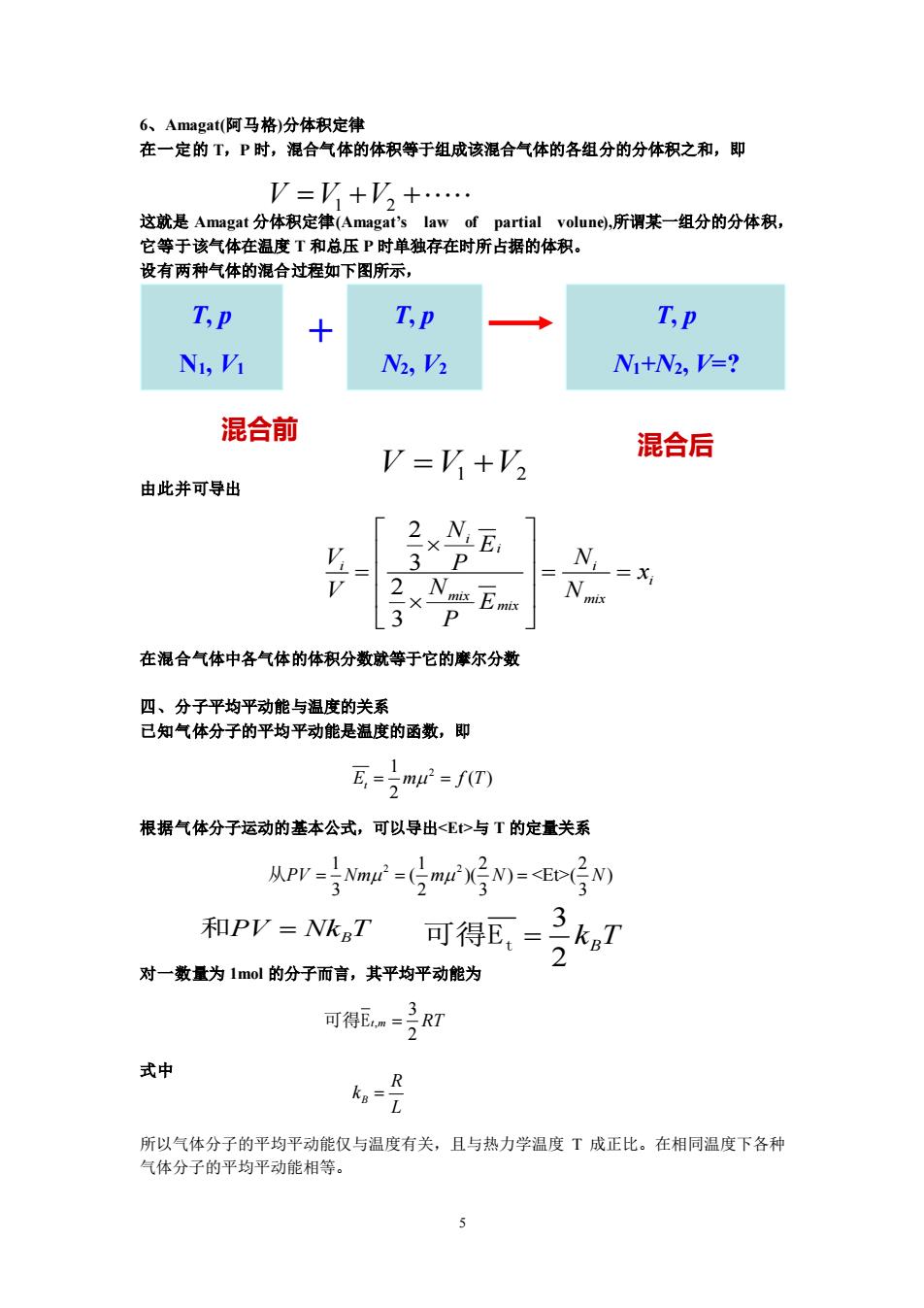
6、Amagate(阿马格)分体积定律 在一定的T,P时,混合气体的体积等于组成该混合气体的各组分的分体积之和,即 V=V+V+. 这就是Amagat分体积定律(Amagat's law of partial volune),所谓某一组分的分体积, 它等于该气体在温度T和总压P时单独存在时所占据的体积。 设有两种气体的混合过程如下图所示, T,p T,P T,p N1,V N2,V2 N1+N2,V=? 混合前 V=V+V2 混合后 由此并可导出 2N, E 31 N 2 =X L31 在混合气体中各气体的体积分数就等于它的摩尔分数 四、分子平均平动能与温度的关系 已知气体分子的平均平动能是温度的函数,即 瓦=mr2=f0 根据气体分子运动的基本公式,可以导出<E>与T的定量关系 从Pr=Nm=(mX号M=P(号NW 和PV=NkaT 对一数量为1m0l的分子而言,其平均平动能为 可得E=多R 式中 ko 所以气体分子的平均平动能仅与温度有关,且与热力学温度T成正比。在相同温度下各种 气体分子的平均平动能相等
5 6、Amagat(阿马格)分体积定律 在一定的 T,P 时,混合气体的体积等于组成该混合气体的各组分的分体积之和,即 这就是 Amagat 分体积定律(Amagat’s law of partial volune),所谓某一组分的分体积, 它等于该气体在温度 T 和总压 P 时单独存在时所占据的体积。 设有两种气体的混合过程如下图所示, 混合前 由此并可导出 在混合气体中各气体的体积分数就等于它的摩尔分数 四、分子平均平动能与温度的关系 已知气体分子的平均平动能是温度的函数,即 根据气体分子运动的基本公式,可以导出<Et>与 T 的定量关系 对一数量为 1mol 的分子而言,其平均平动能为 式中 所以气体分子的平均平动能仅与温度有关,且与热力学温度 T 成正比。在相同温度下各种 气体分子的平均平动能相等。 T, p N1, V1 T, p N2, V2 T, p N1+N2, V=? + V V V = + + 1 2 混合后 V V V = +1 2 2 3 2 3 i i i i i mix mix mix N E V N P x V N N E P = = = 1 2 ( ) 2 E m f T t = = 1 1 2 2 2 2 ( )( ) <Et>( ) 3 2 3 3 从PV Nm m N N = = = 和PV Nk T = B 3 2 B 可得Et = k T , 3 2 可得Et m = RT B R k L =