
物理化学教案 新疆大学化学化工学院物理化学教研室刘月娥 第三章热力学第二定律 3.1自发变化的共同特征一不可逆性 一旦发生就无需借助外力,可以自动进行,这种变化称为自发 变化。 自发变化的共同特征一不可逆性任何自发变化的逆过程是不能自动进行的。例如: 1) 焦耳热功当量中功自动转变成热: 在焦耳的热功当量实 它的逆过程 的温度 物下隆酒样毒热器中的水技拉动从面使水温上开 自动降低而 起不可能自动实现 (2)气体向真空膨胀: 逆过程气体的压缩过程不会自动进行 (3)热量从高温物体传入低温物体: (4浓度不的溶液混合均匀 (⑤)锌片与硫酸铜的置换反 它们的逆过程都不能自动进行。当借助外力,体系恢复原状后,会给环境留下不可磨灭的 影响。 3.2热力学第二定律的表述 克劳修新(Clausius)的说法:“不可能把热从低温物体传到高温物体,而不引起其它变化。” 开尔文(Kn)的说法:“不可能从单一热源取出热使之完全变为功,而不发生其它的变 后来被奥斯特瓦德(Ostward)表述为 二类永动机是不可能造成的”。 第二类永动机:从单一热源吸热使之完全变为功而不留下任何影响。 各种说法完全等价,是人类经验的总结。 注意: (山)并非热不能从低温物体传给高温物体,而是不产生其它变化,如致冷机需要消耗电能。 (2)不能简单理解开尔文说法为 部分 热 功 会部 如理想气体等温膨胀,DU=0,-Q=W,即热全部变为功但气体体积变大了。不引起其它 变化的条件下,热不能全部转化为功 3)第 永动机: 一种能够从 一热源吸热,并将所吸收的热全部变为功而无其它影响的 机器,那是不可能造成的。 热 第三类永动机 功 33卡诺定理 卡诺定理:所有工作于同温热源和同温冷源之间的热机,其效率都不能超过可逆机,即可逆
1 物 理 化 学 教 案 新疆大学化学化工学院物理化学教研室 刘月娥 第三章 热力学第二定律 3.1 自发变化的共同特征—不可逆性 自发变化? 某种变化有自动发生的趋势,一旦发生就无需借助外力,可以自动进行,这种变化称为自发 变化。 自发变化的共同特征—不可逆性 任何自发变化的逆过程是不能自动进行的。例如: (1) 焦耳热功当量中功自动转变成热; 在焦耳的热功当量实验中,重物下降带动搅拌器,量热器中的水被搅动,从而使水温上升。 它的逆过程即水的温度自动降低而重物自动举起不可能自动实现 (2) 气体向真空膨胀; 逆过程气体的压缩过程不会自动进行 (3) 热量从高温物体传入低温物体; (4) 浓度不等的溶液混合均匀; (5) 锌片与硫酸铜的置换反应等, 它们的逆过程都不能自动进行。当借助外力,体系恢复原状后,会给环境留下不可磨灭的 影响。 3.2 热力学第二定律的表述 克劳修斯(Clausius)的说法:“不可能把热从低温物体传到高温物体,而不引起其它变化。” 开尔文(Kelvin)的说法:“不可能从单一热源取出热使之完全变为功,而不发生其它的变 化。” 后来被奥斯特瓦德(Ostward)表述为:“第二类永动机是不可能造成的”。 第二类永动机:从单一热源吸热使之完全变为功而不留下任何影响。 各种说法完全等价,是人类经验的总结。 注 意: (1) 并非热不能从低温物体传给高温物体,而是不产生其它变化,如致冷机需要消耗电能。 (2) 不能简单理解开尔文说法为: 部分 热 功 全部 如理想气体等温膨胀,DU = 0,-Q = W,即热全部变为功但气体体积变大了。不引起其它 变化的条件下,热不能全部转化为功。 (3) 第二类永动机:一种能够从单一热源吸热,并将所吸收的热全部变为功而无其它影响的 机器,那是不可能造成的。 3.3 卡诺定理 卡诺定理:所有工作于同温热源和同温冷源之间的热机,其效率都不能超过可逆机,即可逆

机的效率最大。 卡诺定理推论:所有工作于同温热源与同温冷源之间的可逆机,其热机效率都相等,即与热 机的工作物质无关 卡诺定理的意义:(1)引入了一个不等号原则上解决了化学反应的方向问题:(2)解决 了热机效率的极限值问题。 卡诺定理的证明 证明:设两热源间有可逆热机®)和在意机热机,如右图。调节两热机所作的功相等, 可逆机从高温热源吸热Q,作功,放热(Q-,其效率=-W1Q, 高温热源T 热机 g←形 g 低温热源 不可逆机从高温热源吸Q',作功,放热('-,其效率1=-W/ 反证法:假设川>R 得-W10'>-W12 因W<0;1101'>1/Q 可得 01>0 若把两机联合操作,并把卡诺机逆转,所需的功由不可逆机供给。 循环一周后: 从低温热源吸热: (01-0-(01'-0=01-O1'>0 高温热源得热: 体而没发生其它变化,违反热力号 第二定律。所以原假设1>R不成立;只能R≥ 卡诺定理推论的证明 所有工作于同温热源与同温冷源之间的可逆机,其热机效率都相等,即与热机的工作物 质无 证明:假设有两个不同的卡诺热机A和B,若A为可逆机,按卡诺定理A≥川:但B也 是可逆机,所以B≥:因此只有一种可能A=加 表明:只要两个热源温度一定,不论工作介质是什么物质,也不论其中是pT变化或相变 化、化学变化以及其它任意的变化,它们的热机效率是一样的 3.4的念 摘=(热)火十(热温Q/T商 1,从卡诺循环得到的结论
2 机的效率最大。 卡诺定理推论:所有工作于同温热源与同温冷源之间的可逆机,其热机效率都相等,即与热 机的工作物质无关。 卡诺定理的意义:(1)引入了一个不等号原则上解决了化学反应的方向问题;(2)解决 了热机效率的极限值问题。 卡诺定理的证明 证明:设两热源间有可逆热机(R)和任意机热机(I),如右图。调节两热机所作的功相等, 可逆机从高温热源吸热 Q1,作功 W,放热 (Q1-W) ,其效率 ηR = -W / Q1 不可逆机从高温热源吸 Q1' ,作功 W,放热 (Q1' - W) ,其效率 ηI = -W / Q1' 反证法: 假设 ηI >ηR 得 -W / Q1 ' > -W / Q1 因 W < 0 ;1 / Q1 ' > 1/ Q1 可得 Q1 > Q1' 若把两机联合操作,并把卡诺机逆转,所需的功由不可逆机供给。 循环一周后: 从低温热源吸热 : (Q1 - W) - (Q1' - W) = Q1 - Q1' > 0 高温热源得热 : Q1 -Q1 ' 总结果:热从低温物体传到高温物 体而没发生其它变化,违反热力学 第二定律。所以原假设 ηI >ηR 不成立;只能 ηR≥ηI 卡诺定理推论的证明 所有工作于同温热源与同温冷源之间的可逆机,其热机效率都相等,即与热机的工作物 质无关。 证明:假设有两个不同的卡诺热机 A 和 B,若 A 为可逆机,按卡诺定理 ηA ≥η B;但 B 也 是可逆机,所以 ηB≥ηA;因此只有一种可能 ηA = ηB 表明: 只要两个热源温度一定,不论工作介质是什么物质,也不论其中是 pVT 变化或相变 化、化学变化以及其它任意的变化,它们的热机效率是一样的 3.4 熵的概念 熵 = (热) 火+(热温 Q/T)商 1.从卡诺循环得到的结论
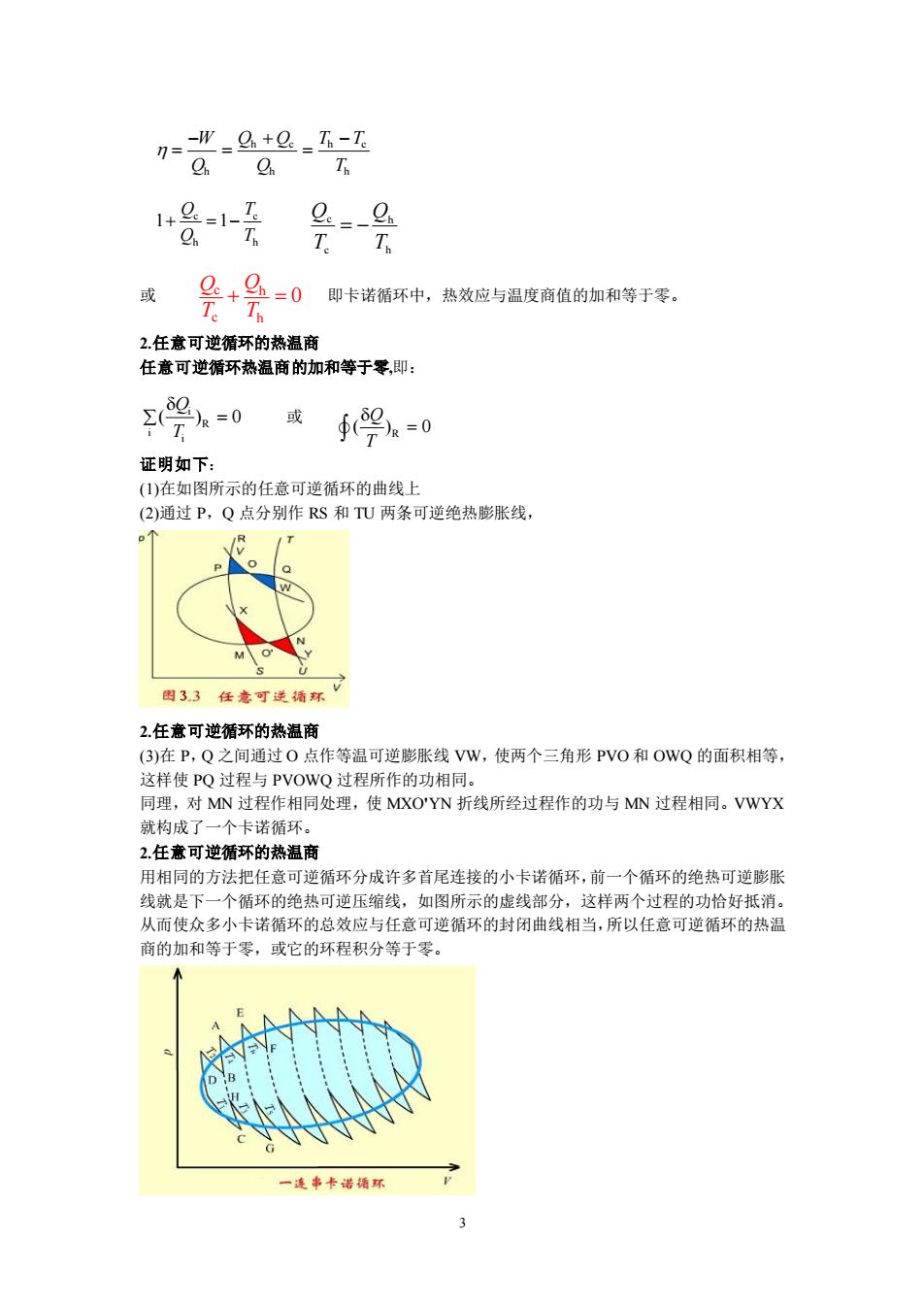
-W_G+e_T-T T 或 +马=0即卡诺循环中,热效应与温度商值的加和等于零 Te Th 2.任意可逆循环的热温商 任意可逆循环热温商的加和等于零,即: =0 或 ∮9n=0 证明如下: (1)在如图所示的任意可逆循环的曲线上 (2)通过P,Q点分别作RS和TU两条可逆绝热膨张线, 33任意可环可 2.任意可逆循环的热温商 (3)在P,Q之间通过O点作等温可逆膨胀线VW,使两个三角形PVO和OWQ的面积相等, 这样使PQ过程与PVOWQ过程所作的功相同。 同理,对MN过程作相同处理,使MXO'YN折线所经过程作的功与MN过程相同。VWYX 就构成了一个卡诺循 2.任意可逆循环的热温商 用相同的方法把任意可逆循环分成许多首尾连接的小卡诺循环,前一个循环的绝热可逆膨胀 线就是下一个循环的绝热可逆压缩线,如图所示的虚线部分,这样两个过程的功恰好抵消。 从而使众多小卡诺循环的总效应与任意可逆循环的封闭曲线相当,所以任意可逆循环的热温 商的加和等于零,或它的环程积分等于零
3 或 即卡诺循环中,热效应与温度商值的加和等于零。 2.任意可逆循环的热温商 任意可逆循环热温商的加和等于零,即: 或 证明如下: (1)在如图所示的任意可逆循环的曲线上 (2)通过 P,Q 点分别作 RS 和 TU 两条可逆绝热膨胀线, 2.任意可逆循环的热温商 (3)在 P,Q 之间通过 O 点作等温可逆膨胀线 VW,使两个三角形 PVO 和 OWQ 的面积相等, 这样使 PQ 过程与 PVOWQ 过程所作的功相同。 同理,对 MN 过程作相同处理,使 MXO'YN 折线所经过程作的功与 MN 过程相同。VWYX 就构成了一个卡诺循环。 2.任意可逆循环的热温商 用相同的方法把任意可逆循环分成许多首尾连接的小卡诺循环,前一个循环的绝热可逆膨胀 线就是下一个循环的绝热可逆压缩线,如图所示的虚线部分,这样两个过程的功恰好抵消。 从而使众多小卡诺循环的总效应与任意可逆循环的封闭曲线相当,所以任意可逆循环的热温 商的加和等于零,或它的环程积分等于零。 或: h c h c h h h W Q Q T T Q Q T − + − = = = c c h h 1 1 Q T Q T + = − h h c c T Q T Q = − c h c h 0 Q Q T T + = i R i i ( ) 0 Q T = R ( ) 0 Q T =

3.熵的引出 用一闭合曲线代表任意可逆循环。 在曲线上任意取A,B两点,把循环分成A,B和BA两个可逆过程。 根据任意可逆循环热温商的公式: f9a=0 可分成两项的加和 a+9=0 3 任意可逆循环 移项得: 9。=9a 说明任意可逆过程的热温商的值决定于始终状态,而与可逆途径无关,这个热温商具有状态 函数的性质。 4.熵的定义 Clausius根据可逆过程的热温商值决定于始终态而与可逆过程无关这一事实定义了“熵 (entropy)这个函数,用符号S表示,单位为J,K 设始、终态A,B的熵分别为和,则: 8-5=A5=9。度4A=号 △5-Σ学。=0对微小安化5=学 几个变的计算式习惯上称为熵的定义式,即嫡的变化值可用可逆过程的热温商值来衡 量 3.5 Clausius不等式与摘增加原理 1.Clausius不等式 设温度相同的两个高、低温热源间有一个可逆机和一个不可逆机。 n-g+2=1+g . 根据卡诺定理: +9<0 T。I
4 3.熵的引出 用一闭合曲线代表任意可逆循环。 在曲线上任意取 A,B 两点,把循环分成 A→B 和 B→A 两个可逆过程。 根据任意可逆循环热温商的公式: 可分成两项的加和 移项得: 说明任意可逆过程的热温商的值决定于始终状态,而与可逆途径无关,这个热温商具有状态 函数的性质。 4.熵的定义 Clausius 根据可逆过程的热温商值决定于始终态而与可逆过程无关这一事实定义了“熵” (entropy)这个函数,用符号“S”表示,单位为 设始、终态 A,B 的熵分别为 和 ,则: 或 对微小变化 这几个熵变的计算式习惯上称为熵的定义式,即熵的变化值可用可逆过程的热温商值来衡 量。 3.5 Clausius 不等式与熵增加原理 1.Clausius 不等式 设温度相同的两个高、低温热源间有一个可逆机和一个不可逆机。 则: 根据卡诺定理: R ( ) 0 Q T = 1 2 B A R R A B ( ) ( ) 0 Q Q T T + = 1 2 B B R R A A ( ) ( ) Q Q T T = B B A R A ( ) Q S S S T − = = R ( )i i i Q S T = R ( ) 0 i i i Q S T − = d ( )R Q S T = h c h h c IR 1 Q Q Q Q Q = + + = h c c R h h 1 T T T T T − = = − c h c h 0 Q Q T T + 1 J K−

R<k则 推广为与多个热源接触的任意不可逆过程得: 设有一个循环,A→B为不可逆过程,B→A为可逆过程,整个循环为不可逆循环。 则有 (②号。+9.<0 9=-s-5>②9 或△SB-∑号An>0 IR B 不可逆循环 如A→B为可逆过程 A.-9=0 将两式合并得Clausius不等式: AS-(∑9.n≥0 δQ是实际过程的热效应,T是环境温度。若是不可逆过程,用>”号,可逆过程用=” 号,这时环境与体系温度相同。 对于微小变化: ds-90或ds82 这些都称为Clausius不等式,也可作为热力学第二定律的数学表达式。 2,熵增加原理 对于绝热体系,δQ=0,所以Clausius不等式为 等号表示绝热可逆过程,不等号表示绝热不可逆过程。熵增加原理可表述为:在绝热条件 下,趋向于平衡的过程使体系的熵增加。或者说在绝热条件下,不可能发生熵减少的过程。 如果是一个孤立体系,环境与体系间既无热的交换,又无功的交换,则熵增加原理可表 述为: 一个孤立体系的熵永不减少 3.Clausius不等式的意义 C1 susius不等式引进的不等号,在热力学上可以作为变化方向与限度的判据。 5
5 则 推广为与多个热源接触的任意不可逆过程得: 设有一个循环, 为不可逆过程, 为可逆过程,整个循环为不可逆循环。 则有 或 如 A→B 为可逆过程 将两式合并得 Clausius 不等式: 是实际过程的热效应,T 是环境温度。若是不可逆过程,用“>”号,可逆过程用“=” 号,这时环境与体系温度相同。 对于微小变化: 或 这些都称为 Clausius 不等式,也可作为热力学第二定律的数学表达式。 2.熵增加原理 对于绝热体系, ,所以 Clausius 不等式为 等号表示绝热可逆过程,不等号表示绝热不可逆过程。熵增加原理可表述为:在绝热条件 下,趋向于平衡的过程使体系的熵增加。或者说在绝热条件下,不可能发生熵减少的过程。 如果是一个孤立体系,环境与体系间既无热的交换,又无功的交换,则熵增加原理可表 述为:一个孤立体系的熵永不减少。 3.Clausius 不等式的意义 Clsusius 不等式引进的不等号,在热力学上可以作为变化方向与限度的判据。 IR R i IR i i ( ) 0 Q T A IR,A B R B i ( ) ( ) 0 Q Q T T → + A R A B B ( ) Q S S T = − B A IR,A B i ( ) Q S S T → − A B IR,A B i ( ) 0 Q S T → → − A B R,A B i ( ) 0 Q S T → → − = A B A B i ( ) 0 Q S T → → − Q d 0 Q S T − d Q S T = Q 0 d 0 S A B → B A →