
一、施肥量与产量之间的关系 1、施肥量与产量之间的直线关系 李比希认为,作物产量与最小养分供应量之间 成直线相关。尤其是在生产条件差,土壤肥力低, 养分供应不足,施肥量较低时。 这种类型一般用 Y=bo+b1X Y-总产量 bo—不施肥区产量 b1-效应系数 X-施肥量
一、施肥量与产量之间的关系 1、施肥量与产量之间的直线关系 李比希认为,作物产量与最小养分供应量之间 成直线相关。尤其是在生产条件差,土壤肥力低, 养分供应不足,施肥量较低时。 这种类型一般用 Y=bo+b1X Y-总产量 bo—不施肥区产量 b1-效应系数 X-施肥量

2、施肥量与产量之间的曲线相关 指数模式 Y=A(1-10-cx ) A-施用该种养分所达最高产量 C-效应系数 二次抛物线函数 Y=b0+b1+b2X2 国内外大量氮肥试验表明,肥料的增产效应往 往符合二次抛物线形式
2、施肥量与产量之间的曲线相关 指数模式 Y=A(1-10-cx ) A-施用该种养分所达最高产量 C-效应系数 二次抛物线函数 Y=b0+b1+b2X2 国内外大量氮肥试验表明,肥料的增产效应往 往符合二次抛物线形式

二、肥料增产效应的阶段性 在一定生产条件下,当作物严重缺乏 某种养分时,增施该养分的增产量,起初 往往是递增,但超过一定限度后,增施单 位剂量养分的增产量便开始递减,当其递 减为零时,作物产量达到最大值,此时, 再继续增加肥料,则将导致减产
二、肥料增产效应的阶段性 在一定生产条件下,当作物严重缺乏 某种养分时,增施该养分的增产量,起初 往往是递增,但超过一定限度后,增施单 位剂量养分的增产量便开始递减,当其递 减为零时,作物产量达到最大值,此时, 再继续增加肥料,则将导致减产
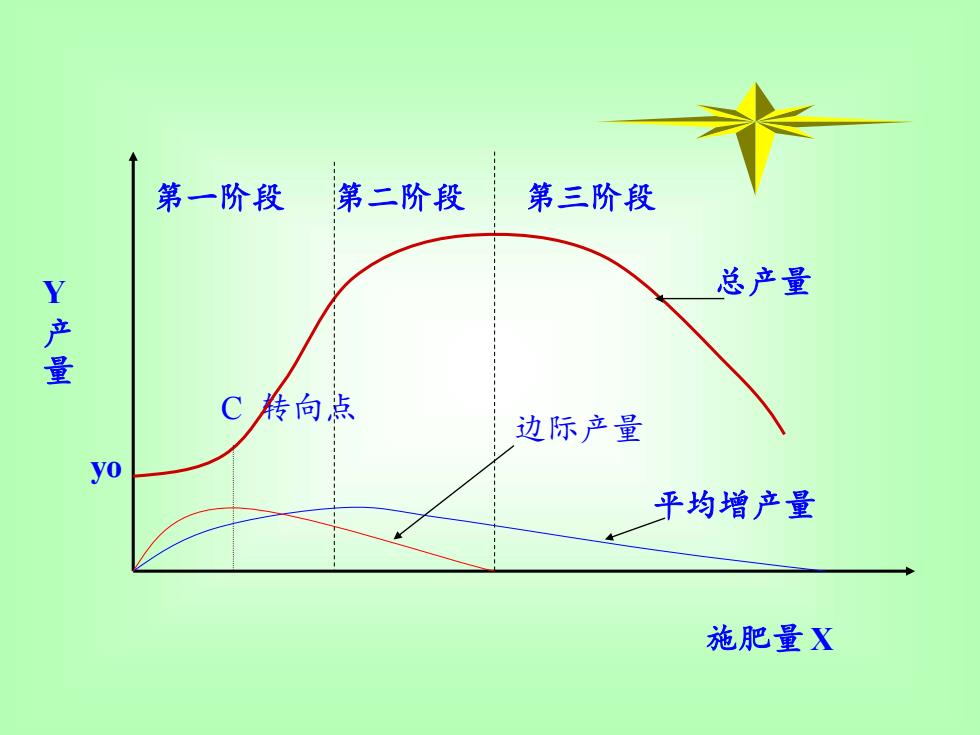
第一阶段 第二阶段 第三阶段 总产量 C 转向点 边际产量 平均增产量 Y 产 量 施肥量 X yo
第一阶段 第二阶段 第三阶段 总产量 C 转向点 边际产量 平均增产量 Y 产 量 施肥量 X yo

1、在土壤供肥水平低的情况下,增施单位剂量肥料的 增产量(即边际产量)随施肥量的增加而递增,直至转 向点(C)时为止。 2、超过转向点后,增施单位剂量肥料的增产量随施肥 量的增加而递减,因而总产量按报酬递减率增加,直达 到最高产量为止。 3、在一定生产条件下,作物有一最高产量,超过最高 产量后,继续增加肥料,则总产量随施肥的增加而递减, 出现负效应,但是总产量的递减率可能小于到达最高产 量的递增率。 4、无限量的增施肥料,可能使产量下降为零。 根据以上特点,可将肥料增产效应划分成三个阶段,即 由三个最高点反映了曲线三阶段
1、在土壤供肥水平低的情况下,增施单位剂量肥料的 增产量(即边际产量)随施肥量的增加而递增,直至转 向点(C)时为止。 2、超过转向点后,增施单位剂量肥料的增产量随施肥 量的增加而递减,因而总产量按报酬递减率增加,直达 到最高产量为止。 3、在一定生产条件下,作物有一最高产量,超过最高 产量后,继续增加肥料,则总产量随施肥的增加而递减, 出现负效应,但是总产量的递减率可能小于到达最高产 量的递增率。 4、无限量的增施肥料,可能使产量下降为零。 根据以上特点,可将肥料增产效应划分成三个阶段,即 由三个最高点反映了曲线三阶段