
第一节核外电子运动状态及特性三.测不准原理(uncertaintyprinciple)Heisenberg指出,无法同时确定微观粒子的位置和动量:△x·Ap≥h/4元△x为粒子在x方向的位置误差,△p为动量在x方向的误差。由于h是极小的量,所以△x越小△p越大,反之亦然。测不准原理是粒子波动性的结果,意味着微观粒子运动不存在既确定位置又有确定速度的运动轨迹
第一节 核外电子运动状态及特性 三. 测不准原理(uncertainty principle) Heisenberg指出,无法同时确定微观粒子 的位置和动量: △x ·△px≥h/4π △x为粒子在x方向的位置误差,△px为动量在x 方向的误差。由于h是极小的量,所以△x越小, △px越大,反之亦然。测不准原理是粒子波动 性的结果,意味着微观粒子运动不存在既确定 位置又有确定速度的运动轨迹

第一节核外电子运动状态及特性例电电子在原子核附近运动的速度约6×106m·s-l5原子半径约10-10m。若速度误差为土1%,电子的位置误差△x有多大?解Av=6×106ms-l×0.01=6×104ms-l,h=6.626×10-34kg?m2.s-l:根据测不准原理:6.626×10-34kg·m2.s-lh=1×10-mAx≥4元×9.1×10-3kg×6×10m.sl4mv即原子中电子的位置误差比原子半径大10倍电子在原子中无精确的位置可言
第一节 核外电子运动状态及特性 例 电子在原子核附近运动的速度约6×106 m·s-1 , 原子半径约10-10 m。若速度误差为±1%,电子 的位置误差△x有多大? 解 △v = 6×106 m·s-1×0.01 = 6×104 m·s-1 , h = 6.626×10-34kg·m2·s-1;根据测不准原理: 即原子中电子的位置误差比原子半径大10倍, 电子在原子中无精确的位置可言。 1 10 m 4 9.1 10 kg 6 10 m s 6.626 10 kg m s 4 Δ Δ 9 -31 4 -1 34 2 -1 − − = = m h x

第二节氢原子的波函数一.量子数1.波函数(wave function)原子中电子具有波动性,奥地利物理学家Schrodinger导出Schrodinger方程,方程的解是波函数业,用来描述电子的运动状态2.lP的意义本身物理意义并不明确,但12却有明确的物理意义。表示在原子核外空间某点处电子出现的概率密度(probabilitydensity),即在该点处单位体积中电子出现的概率
第二节 氢原子的波函数 一. 量子数 1. 波函数ψ (wave function) 原子中电子具有波动性,奥地利物理学家 Schrödinger导出Schrödinger方程,方程的解是 波函数ψ ,用来描述电子的运动状态。 2. |ψ | 2的意义 ψ本身物理意义并不明确,但|ψ | 2却有明确 的物理意义。表示在原子核外空间某点处电子 出现的概率密度(probability density),即在 该点处单位体积中电子出现的概率
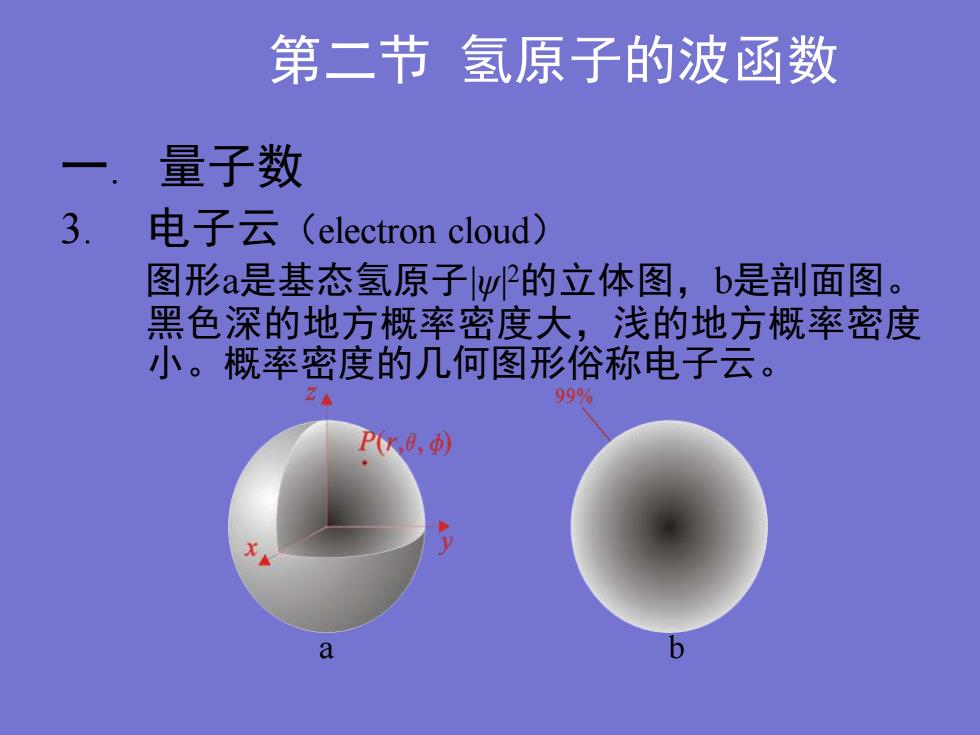
第二节氢原子的波函数一.量子数3.电子云(electron cloud)图形a是基态氢原子l的立体图,b是部面图黑色深的地方概率密度大,浅的地方概率密度小。概率密度的几何图形俗称电子云。99%P(r.e,o)a
第二节 氢原子的波函数 一. 量子数 3. 电子云(electron cloud) 图形a是基态氢原子|ψ| 2的立体图,b是剖面图。 黑色深的地方概率密度大,浅的地方概率密度 小。概率密度的几何图形俗称电子云。 a b

第二节氢原子的波函数一.量子数4.原子轨道(atomicorbital)描述原子中单个电子运动状态的波函数中常称作原子轨道。原子轨道仅仅是波函数的代名词,绝无经典力学中的轨道含义。严格地说原子轨道在空间是无限扩展的,但一般把电子出现概率在99%的空间区域的界面作为原子轨道的大小
第二节 氢原子的波函数 一. 量子数 4. 原子轨道(atomic orbital) 描述原子中单个电子运动状态的波函数ψ 常称作原子轨道。原子轨道仅仅是波函数的代 名词,绝无经典力学中的轨道含义。严格地说 原子轨道在空间是无限扩展的,但一般把电子 出现概率在99%的空间区域的界面作为原子轨 道的大小