第一节核外电子运动状态及特性一.氢光谱和氢原子的玻尔(Bohr)模型2.氢原子的线状光谱(linespectrum)白光散射时,观察到可见光区的连续光谱,但H原子受激发射所得光谱却是不连续的线状光谱,在可见光区有四条谱线WZO400450500550600650700750A/nm
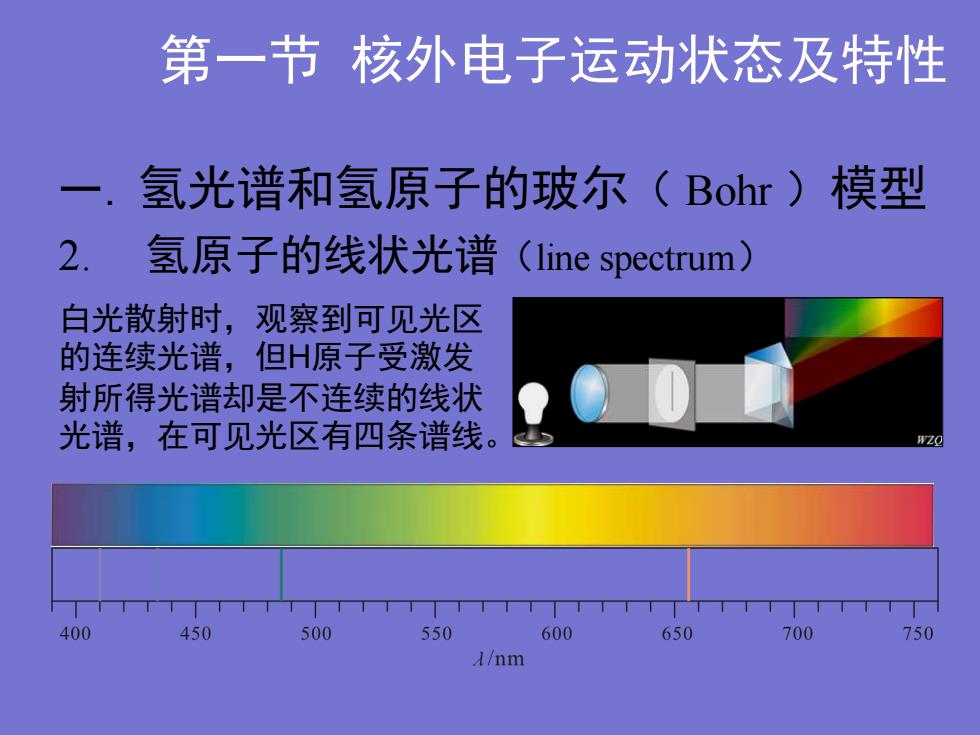
第一节 核外电子运动状态及特性 一. 氢光谱和氢原子的玻尔( Bohr )模型 2. 氢原子的线状光谱(line spectrum) 白光散射时,观察到可见光区 的连续光谱,但H原子受激发 射所得光谱却是不连续的线状 光谱,在可见光区有四条谱线

第一节核外电子运动状态及特性一.氢光谱和氢原子的玻尔(Bohr)模型3.氢光谱的波长规律L=RH元niO式中,入是波长,n为正整数,且n2大于n1。Rμ = 1.096776 ×107 m-1
第一节 核外电子运动状态及特性 一. 氢光谱和氢原子的玻尔( Bohr )模型 3. 氢光谱的波长规律 = − 2 2 2 1 H 1 ~ 1 1 n n R 7 1 H 1.096776 10 m ~ − R = 式中,λ是波长,n为正整数,且n2大于n1

第一节核外电子运动状态及特性一.氢光谱和氢原子的玻尔(Bohr)模型4Bohr的氢原子模型入电子沿固定轨道绕核运动不吸收也不辐射能量,称为定态。轨道能量称为能级。RE:-(eV)-13.62nnn=1时能量最低,为基态其它能量较高的状态都称主量子数n=1,2,3....。为激发态
第一节 核外电子运动状态及特性 4. Bohr 的氢原子模型 ① 电子沿固定轨道绕核运动, 不吸收也不辐射能量,称 为定态。轨道能量称为能 级。 主量子数n=1, 2, 3,.。 n =1时能量最低,为基态, 其它能量较高的状态都称 为激发态。 一. 氢光谱和氢原子的玻尔( Bohr )模型 (eV) 1 13.6 2 2 n n R E = − = −

第一节核外电子运动状态及特性一.氢光谱和氢原子的玻尔(Bohr)模型Bohr的氢原子模型4.2原子由一种定态(能级E1)跃迁到另一种定态(能级E2)。吸收能量辐射能量跃迁所吸收或辐射光子的能量等于跃迁前后能级的能量差:n-4n-3n-2m-E=RHAE=hV=|E2-E11E=-0.25RHE=-0.11R普朗克常量h=6.626×10-34J·S,E=-0.062Rv是光子频率
第一节 核外电子运动状态及特性 4. Bohr 的氢原子模型 ② 原子由一种定态(能级E1)跃迁到 另一种定态(能级E2)。 跃迁所吸收或辐射光子的能量等于 跃迁前后能级的能量差: ΔE = hν = | E2 –E1 | 普朗克常量 h = 6.626×10-34 J·s, ν是光子频率。 一. 氢光谱和氢原子的玻尔( Bohr )模型

第一节核外电子运动状态及特性一.氢光谱和氢原子的玻尔(Bohr)模型4.Bohr的氢原子模型Bohr运用量子化观点,成功地解释了氢原子的稳定性和不连续光谱。但未能冲破经典物理学的束缚,不能解释多电子原子光谱,甚至不能说明氢原子光谱的精细结构。Bohr理论属于旧量子论。电子等微观粒子的运动不遵守经典物理学规律,必须用量子力学方法来描述
第一节 核外电子运动状态及特性 一. 氢光谱和氢原子的玻尔( Bohr )模型 4. Bohr 的氢原子模型 Bohr运用量子化观点,成功地解释了氢原子的 稳定性和不连续光谱。但未能冲破经典物理学 的束缚,不能解释多电子原子光谱,甚至不能 说明氢原子光谱的精细结构。Bohr理论属于旧 量子论。电子等微观粒子的运动不遵守经典物 理学规律,必须用量子力学方法来描述