
36 第2章模型评估与选择 回顾前面介绍的一些性能度量可看出,它们大都隐式地假设了均等代价, 例如式(2.4)所定义的错误率是直接计算“错误次数”,并没有考虑不同错误会 造成不同的后果.在非均等代价下,我们所希望的不再是简单地最小化错误次 数,而是希望最小化“总体代价”(total cost).若将表2.2中的第0类作为正 类、第1类作为反类,令D+与D-分别代表样例集D的正例子集和反例子 集,则“代价敏感”(cost-sensitive)错误率为 E(f;D;cost)= I(f(e)≠h)×costo1 +∑I()≠)×cost0 (2.23) ED- 类似的,可给出基于分布定义的代价敏感错误率,以及其他一些性能度量 如精度的代价敏感版本.若令cost,中的、j取值不限于0、1,则可定义出多 分类任务的代价敏感性能度量 在非均等代价下,ROC曲线不能直接反映出学习器的期望总体代价,而 参见习题2.7. “代价曲线”(cost curve)则可达到该目的.代价曲线图的横轴是取值为0,刂 的正例概率代价 P(+)cost px costor p×costo1+(1-p)×cost10】 (2.24) 规范化” ion)是将不皮化花图的 其中p是样例为正例的概率:纵轴是取值为0,刂的归一化代价 佳映射到相同的围定范三 中,常见的是0,,此时亦 称“归一化”,参见习题 cotmENRx px costo+FPRx(1-p) (2.25) 2.8. p×costo1+(1-p)×cost0 其中FPR是式(2.19)定义的假正例率,FNR=1-TPR是假反例率.代价曲线 的绘制很简单:ROC曲线上每一点对应了代价平面上的一条线段,设ROC曲 线上点的坐标为(TPR,FPR),则可相应计算出FNR,然后在代价平面上绘制 一条从(O,FPR)到(L,FNR)的线段,线段下的面积即表示了该条件下的期望 总体代价;如此将ROC曲线上的每个点转化为代价平面上的一条线段,然后 取所有线段的下界,围成的面积即为在所有条件下学习器的期望总体代价,如 图2.5所示

2.4比较检验 1.0 05 FNR 代价曲线 期望总体代价 正例概率代价 1.0 图2.5代价曲线与期望总体代价 2.4比较检验 有了实验评估方法和性能度量,看起来就能对学习器的性能进行评估比较 了:先使用某种实验评估方法测得学习器的某个性能度量结果,然后对这些结 果进行比较.但怎么来做这个“比较”呢?是直接取得性能度量的值然后“比 大小”吗?实际上,机器学习中性能比较这件事要比大家想象的复杂得多.这 里面涉及几个重要因素:首先,我们希塑比较的是泛化性能,然而通过实验评估 方法我们获得的是测试集上的性能,两者的对比结果可能未必相同;第二,测试 集上的性能与测试集本身的选择有很大关系,且不论使用不同大小的测试集会 得到不同的结果,即便用相同大小的测试集,若包含的测试样例不同,测试结果 也会有不同;第三,很多机器学习算法本身有一定的随机性,即便用相同的参数 设置在同一个测试集上多次运行,其结果也会有不同.那么,有没有适当的方法 对学习器的性能进行比较呢? 统计假设检验(hypothesis test)为我们进行学习器性能比较提供了重要依 据.基于假设检验结果我们可推断出,若在测试集上观察到学习器A比B好 则A的泛化性能是否在统计意义上优于B,以及这个结论的把握有多大.下面 更多关于假设检验的介 绍可参见NeIIck,2010. 我们先介绍两种最基本的假设检验,然后介绍几种常用的机器学习性能比较方 法.为便于讨论,本节默认以错误率为性能度量,用€表示. 2.4.1假设检验 假设检验中的“假设”是对学习器泛化错误率分布的某种判断或猜想,例 如“=0”,现实任务中我们并不知道学习器的泛化错误率,只能获知其测试错 误率.泛化错误率与测试错误率未必相同,但直观上,二者接近的可能性应比
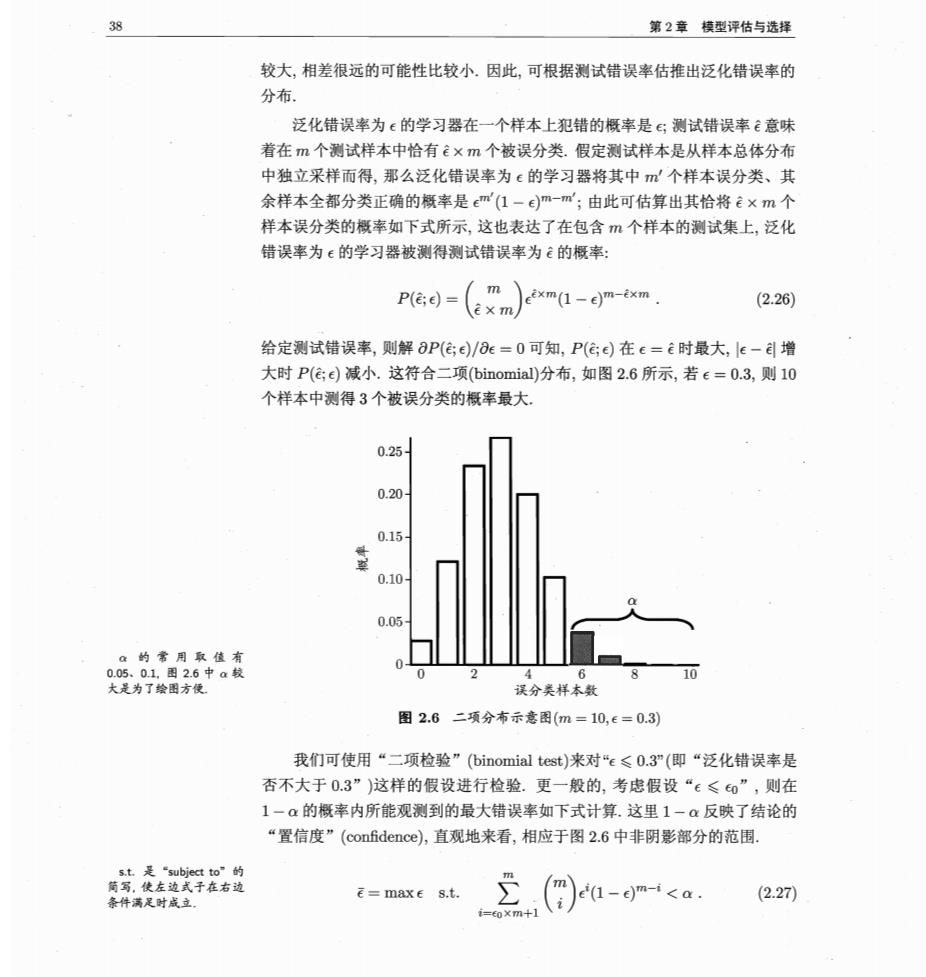
第2章模型评估与选择 较大,相差很远的可能性比较小.因此,可根据测试错误率估推出泛化错误率的 分布 泛化错误率为€的学习器在一个样本上犯错的概率是€:测试错误率意味 着在m个测试样本中恰有×m个被误分类.假定测试样本是从样本总体分布 中独立采样而得,那么泛化错误率为€的学习器将其中m个样本误分类、其 余样本全都分类正确的概率是(1一e)m-m';由此可估算出其恰将×m个 样本误分类的概率如下式所示,这也表达了在包含m个样本的测试集上,泛化 错误率为€的学习器被测得测试错误率为的概率: Pee=(m)exm-em-xm e×m/ (2.26) 给定测试错误率,则解8P(Ge)/e=0可知,P(Ge)在e=e时最大,le-自增 大时P(Ge)减小.这符合二项binomial)分布,如图2.6所示,若e=0.3,则10 个样本中测得3个被误分类的概率最大 0.25 0.20 0.15 0.10 0.05 10 误分类样本数 图2.6二项分布示意图(m=10,e=0.3) 我们可使用“二项检验”(binomial test)来对“e≤0.3”(即“泛化错误率是 否不大于03”)这样的假设进行检验.更一般的,考虑假设“€≤0”,则在 1一α的概率内所能观测到的最大错误率如下式计算.这里1-α反映了结论的 “置信度”(confidence),直观地来看,相应于图2.6中非阴影部分的范围. 两药麦于拉市数 条件满足时成立 E=maxe s.t. £(a-ga (2.27)
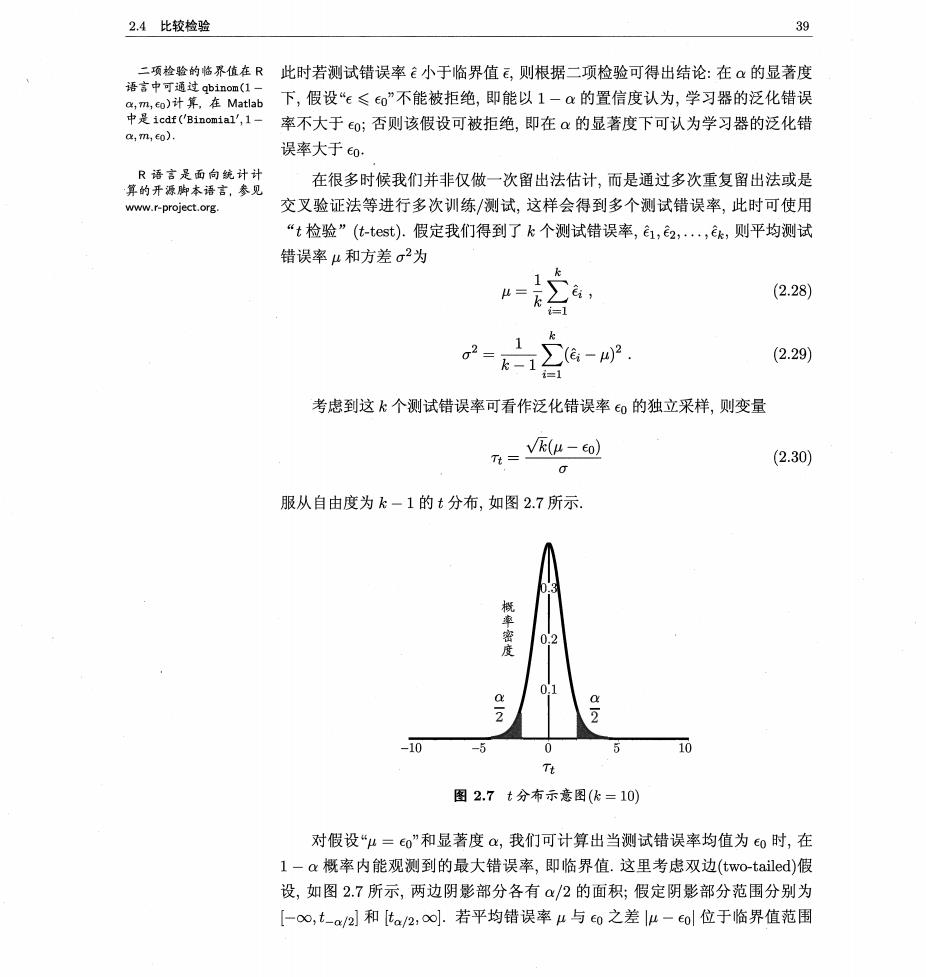
2.4比较检验 39 此时若测试错误率小于临界值飞,则根据二项检验可得出结论:在α的显著度 中设on 下,假设“≤e0”不能被拒绝,即能以1一α的置信度认为,学习器的泛化错误 率不大于o;否则该假设可被拒绝,即在α的显著度下可认为学习器的泛化错 a,m,0) 误率大于0 R语言是面向统计计 算的开源脚本语言,参见 在很多时候我们并非仅做一次留出法估计,而是通过多次重复留出法或是 www.r-project.org. 交叉验证法等进行多次训练/测试,这样会得到多个测试错误率,此时可使用 “t检验”(t-tst).假定我们得到了k个测试错误率,1,2,,k,则平均测试 错误率4和方差σ2为 = (2.28) 02=k-1 1 (-)2 (2.29) 考虑到这k个测试错误率可看作泛化错误率0的独立采样,则变量 T=VE(u-eo) (2.30) 服从自由度为k-1的t分布,如图2.7所示 10 10 图2.7t分布示意图(k=10) 对假设“μ=o”和显著度a,我们可计算出当测试错误率均值为0时,在 1-a概率内能观测到的最大错误率,即临界值.这里考虑双边(two-tailed)假 设,如图2.7所示,两边阴影部分各有α/2的面积;假定阴影部分范围分别为 【-oo,t-a/2l和[a/2,o∞.若平均错误率4与0之差lμ-0l位于临界值范围

第2章模型评估与选择 [t-a2,t/2l内,则不能拒绝假设“μ=o”,即可认为泛化错误率为co,置信度为 1一a;否则可拒绝该假设,即在该显著度下可认为泛化错误率与0有显著不 同.α常用取值有0.05和0.1.表2.3给出了一些常用临界值。 表2.3双边t检验的常用临界值 k 2 5102030 上面介绍的两种方法都是对关于单个学习器泛化性能的假设进行检验,而 在现实任务中,更多时候我们需对不同学习器的性能进行比较,下面将介绍适 用于此类情况的假设检验方法。 2.4.2交叉验证t检验 对两个学习器A和B,若我们使用k折交叉验证法得到的测试错误率分 别为,兮,,和导,喝,,呢,其中e和e孕是在相同的第i折训练/测 试集上得到的结果,则可用k折交叉验证“成对t检验”(paired t-tests)来进行 比较检验.这里的基本思想是若两个学习器的性能相同,则它们使用相同的训 练/测试集得到的测试错误率应相同,即c= 具体来说,对k折交叉验证产生的k对测试错误率:先对每对结果求差 △:=4-甲;若两个学习器性能相同,则差值均值应为零.因此,可根据差值 △1,△2,,△k来对“学习器A与B性能相同”这个假设做t检验,计算出差值 的均值4和方差g2,在显著度α下,若变量 T= V (2.31) 小于临界值。/2,k-1,则假设不能被拒绝,即认为两个学习器的性能没有显著差 别;否则可认为两个学习器的性能有显著差别,且平均错误率较小的那个学习 器性能较优.这里t。/2,k-1是自由度为k-1的t分布上尾部累积分布为a/2 的临界值 欲进行有效的假设检验,一个重要前提是测试错误率均为泛化错误率的独 立采样.然而,通常情况下由于样本有限,在使用交叉验证等实验估计方法时 不同轮次的训练集会有一定程度的重叠,这就使得测试错误率实际上并不独立 会导致过高估计假设成立的概率.为缓解这一问题,可采用“5×2交叉验证