2015/10/21 二阶(2 nd order)系统-实例 手一x School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 阶系统的模型表达 C(s) o Undamped natural frequency 无阻尼自然频率 R(s)s2+25os+02 Damping ratio R(s) C(s) 阻尼比 s(3+20.) D(s)=s2+250ns+o=0 R2=-50n±onV52-1 R=-8±aPi Img. 5<1 欠阻尼(Underdamped):O<Cl =1 5>1 P=-0 临界阻尼(Critically damped):G=l 过阻尼(Overdamped):G>l Real R=-9±jm-g 无阻尼(undamped):=O 负阻尼*:S<0 月,=±j0 School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 6
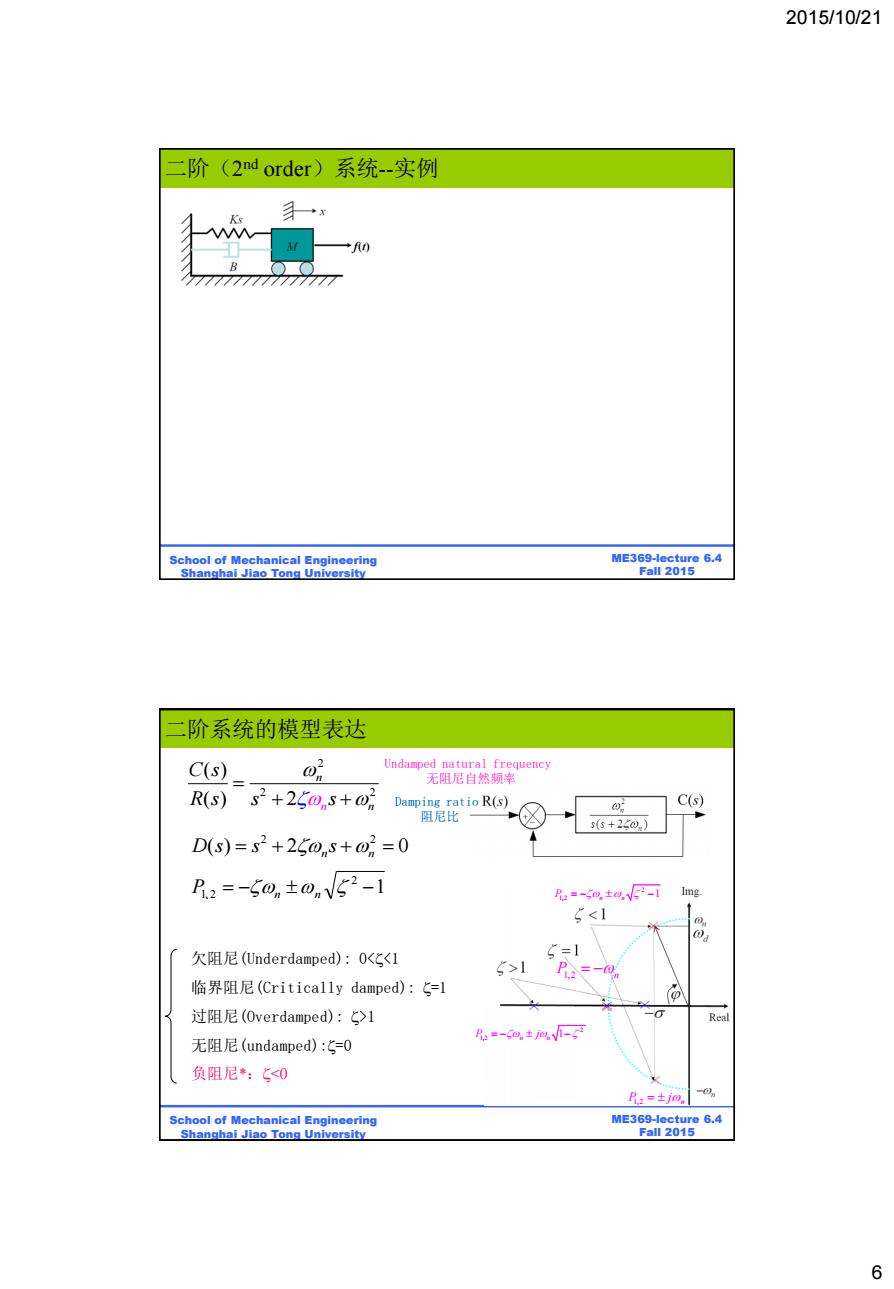
2015/10/21 6 ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 二阶(2 nd order)系统--实例 ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 2 2 2 ( ) ( ) 2 n n n C s R s s s 2 2 ( ) 2 0 D s s sn n 1 2 P1、2 n n 2 1,2 1 P j n n P1,2 n 2 1,2 1 P n n P j 1,2 n 欠阻尼(Underdamped): 0<<1 临界阻尼(Critically damped): =1 过阻尼(Overdamped): >1 无阻尼(undamped):=0 负阻尼*:<0 Undamped natural frequency 无阻尼自然频率 Damping ratio 阻尼比 二阶系统的模型表达
2015/10/21 阶系统一单位阶跃响应(0<<1) 欠阻尼0<C<1 B2=-50n±j0.V1-52=-5@n±jo e R(s)= c(t0=1- sin(@+B),(t20) B-arctan V-2 5 0g=0nV-52 c(t) "damped nature frequency" 286 “阻尼自然频率” 6=02 →衰减的振荡) 420 1)衰减快慢 ←g,wn 8 品Q8 0.6 2)振荡幅值个 ←?↓ 4 02 10 15 →ep=0 School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 阶系统一单位阶跃响应(0<<1) (续) C(s) 回n C(s) 1 R(s) s2+250w5+可 R(s)Ts+1 e-soy c(t)=1- =sin(oal+B),(t≥0) cu)=1-eT,(1≥0 s平面 j B米----- m=m,1- j@4 s平面 P.X 衰减系数 衰减系数 Con 1/T School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 7
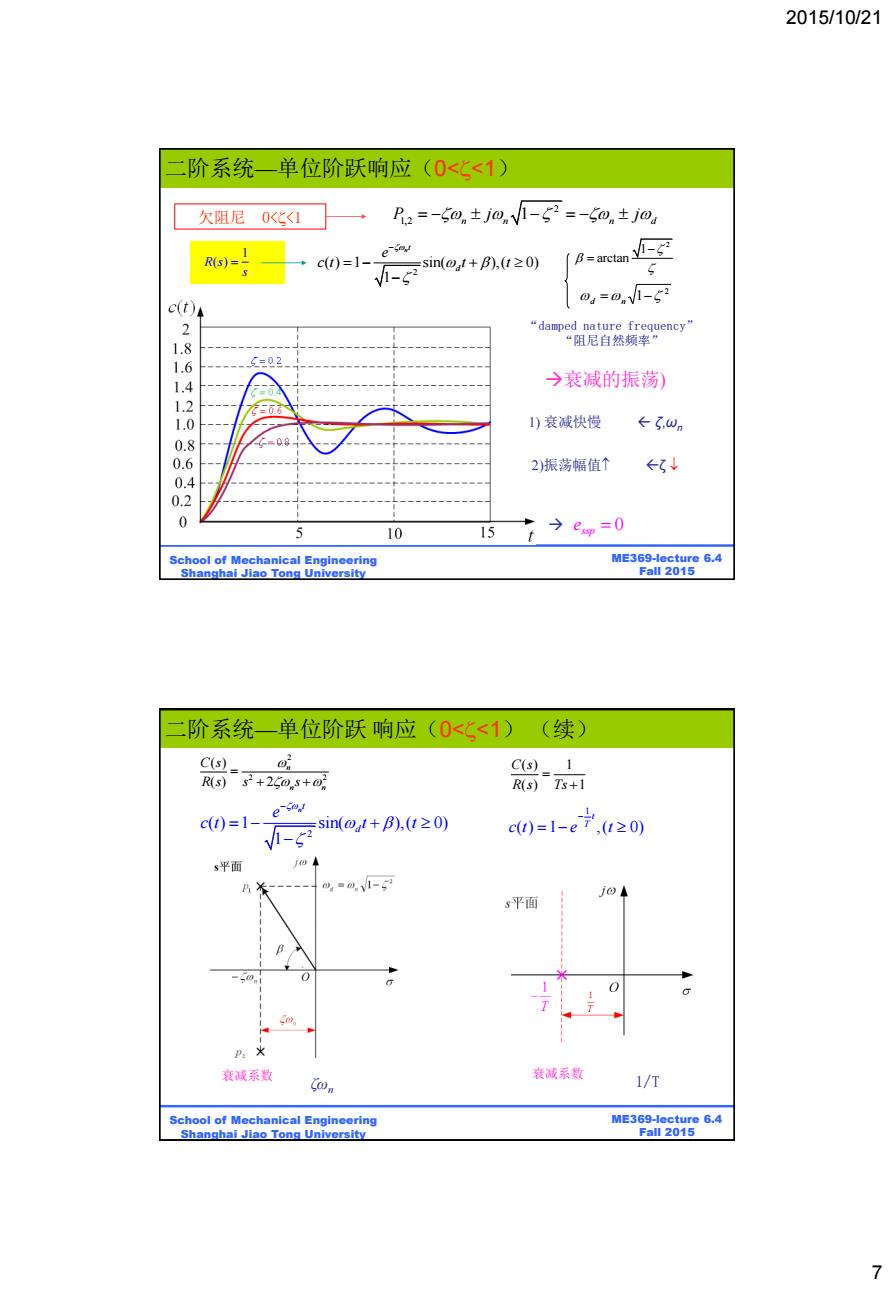
2015/10/21 7 ME369-lecture 6.4 Fall 2015 二阶系统—单位阶跃响应(0<<1) School of Mechanical Engineering Shanghai Jiao Tong University 欠阻尼 0<<1 2 1,2 1 P j j n n n d 2 d n 1 “damped nature frequency” “阻尼自然频率” 1 R s( ) s 2 1 arctan 衰减的振荡) 0 ssp e 2)振荡幅值 1) 衰减快慢 2 ( ) 1 sin( ),( 0) 1 n t d e c t t t ζ,ωn ζ ME369-lecture 6.4 Fall 2015 二阶系统—单位阶跃 响应(0<<1) (续) School of Mechanical Engineering Shanghai Jiao Tong University ζωn 1 ( ) 1 ,( 0) t T c t e t 1/T 2 ( ) 1 sin( ),( 0) 1 n t d e c t t t 2 2 2 ( ) ( ) 2 n n n C s R s s s ( ) 1 ( ) 1 C s R s Ts 衰减系数 衰减系数
2015/10/21 阶系统一单位阶跃响应(《=0) 无阻尼 R.2=±j0n G=0 =} c(t)=1-cos01,(t≥0) c(t) 衰减系数=0 1 1.6 20 s平面 8 0.4 0.2 0 5 10 15 →等幅振荡 无阻尼自然频率m School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 阶系统一单位阶跃响应(=1) 临界阻尼 51 2=-0m ct)=1-e(1+o),(t≥0) R)=5 c(t) s平面 jo 1.6 1.4 1.2 PiP2 1.0 0 8 0.6 .4 0.2 50,=0m 0 5 10 15 单调上升,无振荡、无超调 衰减系数 Con=On y = School of Mechanical Engineering ME369-lecture 6.4 Shanghai Jiao Tong University Fall 2015 8
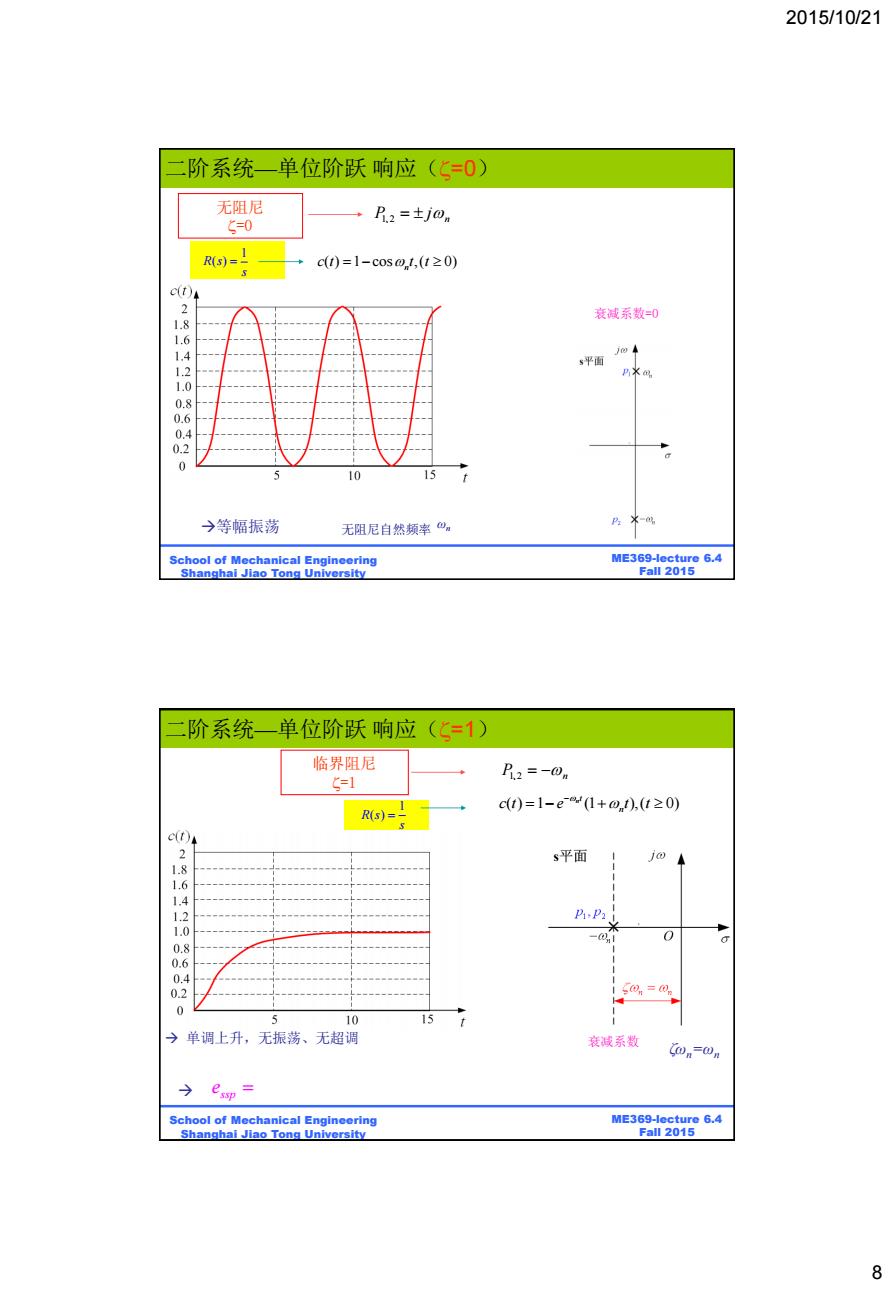
2015/10/21 8 ME369-lecture 6.4 Fall 2015 二阶系统—单位阶跃 响应(=0) School of Mechanical Engineering Shanghai Jiao Tong University 无阻尼 =0 、 n P1 2 j ωn 1 R s( ) s ( ) 1 cos ,( 0) n c t t t 等幅振荡 衰减系数=0 无阻尼自然频率 ME369-lecture 6.4 Fall 2015 School of Mechanical Engineering Shanghai Jiao Tong University 临界阻尼 =1 P1、2 n ( ) 1 (1 ),( 0) n t n c t e t t 单调上升,无振荡、无超调 1 R s( ) s ssp e ζωn=ωn 衰减系数 二阶系统—单位阶跃 响应(=1)