电子科技大学：《机器学习 Machine Learning》课程教学资源（课件讲稿）第4章 回归分类

线性分类 w ,线性分类器 X w 。扩展权向量 y=(w')x' 0 1◇ W'=

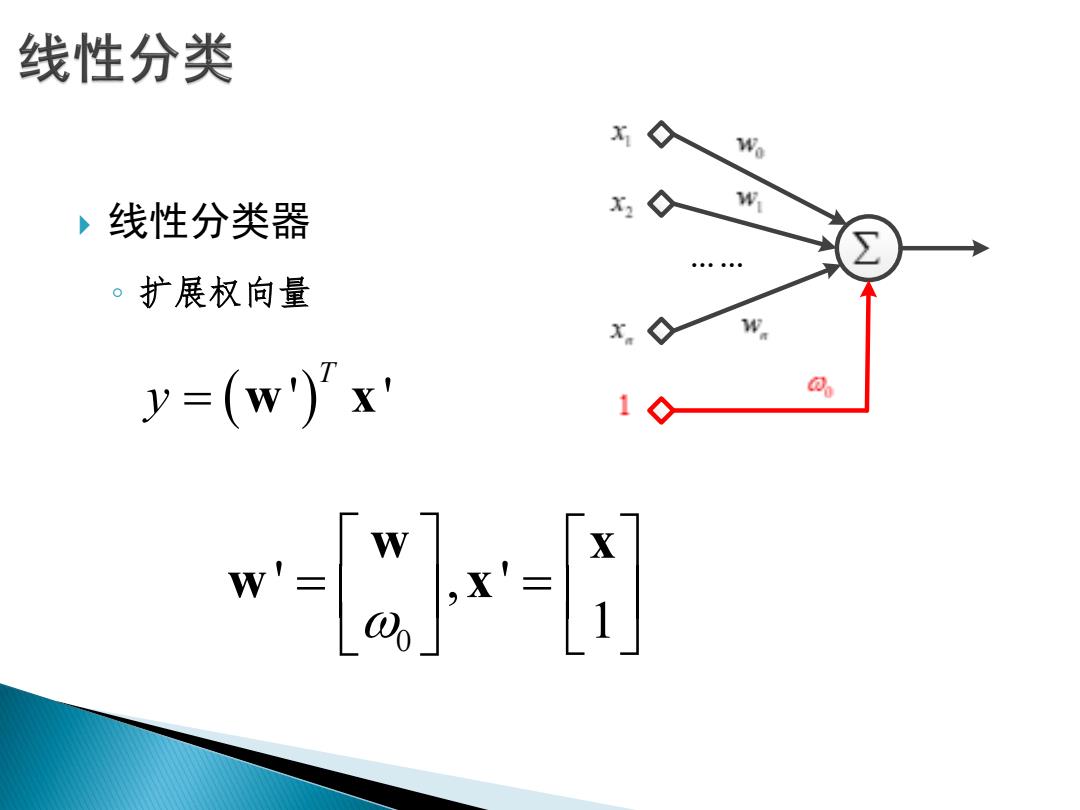
 线性分类器 ◦ 扩展权向量  ' '  T y  w x 0 ' , '  1               w x w x

线性分类 ，最小二乘解一一矩阵法 。给定样本{飞，y},乃={-1,1，构造矩阵Φ 起 x81… Φ= W w=(w'Φ)'Φ'y

 最小二乘解——矩阵法 ◦ 给定样本 ，构造矩阵Ф [1] [2] [ ] 1 1 1 1 [1] [2] [ ] 2 2 2 2 [1] [2] [ ] ... ... ... ... ... K K K N N N N x x x x x x x x x                x x x   1 T T  w y     xi i i , , { 1,1} y y   

close all clear all 线性分类 clc Obj1.NTrain 100; 0bj1.mean=2.5*[3;51: Obj1.SampTrain randn(2,Obj1.NTrain)+ kron(Obj1.mean,ones(1,Obj1.NTrain)): Obj1.NTest 100; Obj1.SampTest randn(2,Obj1.NTest)+ 最小二乘解 kron(Obj1.mean,ones(1,Obj1.NTest)); Obj2.NTrain 100; 16 0bj2.mean=-0.0*[3:51: Obj2.SampTrain randn(2,Obj2.NTrain)+ TestMatrix kron(Obj2.mean,ones(1,Obj2.NTrain)); Obj2.NTest 100; Obj2.SampTest randn(2,Obj2.NTest)+ kron(Obj2.mean,ones(1,Obj2.NTest)); 1 0 LMS 0 TestMatrix zeros(2); cnt_cl 1; cnt_c2 =1; t=1:1000: tt=(t-500)*0.01: figure; TestMatrix plot(Obj1.SampTrain(1,:)Obj1.SampTrain(2,:), 'ro','linewidth',2,'markersize',10) hold on; 0.9500 0.0500 plot(Obj2.SampTrain(1,:)Obj2.SampTrain(2,:) 'bo','linewidth',2,'markersize',10) 0.1400 0.8600 cnt 1; X zeros(Obj1.NTrain Obj2.NTrain,3); for iii =1:Obj1.NTrain X(cnt,1 2)=Obj1 .SampTrain(:,iii); X(cnt,3)=1: ycnt,1)=1: cntcnt 1;

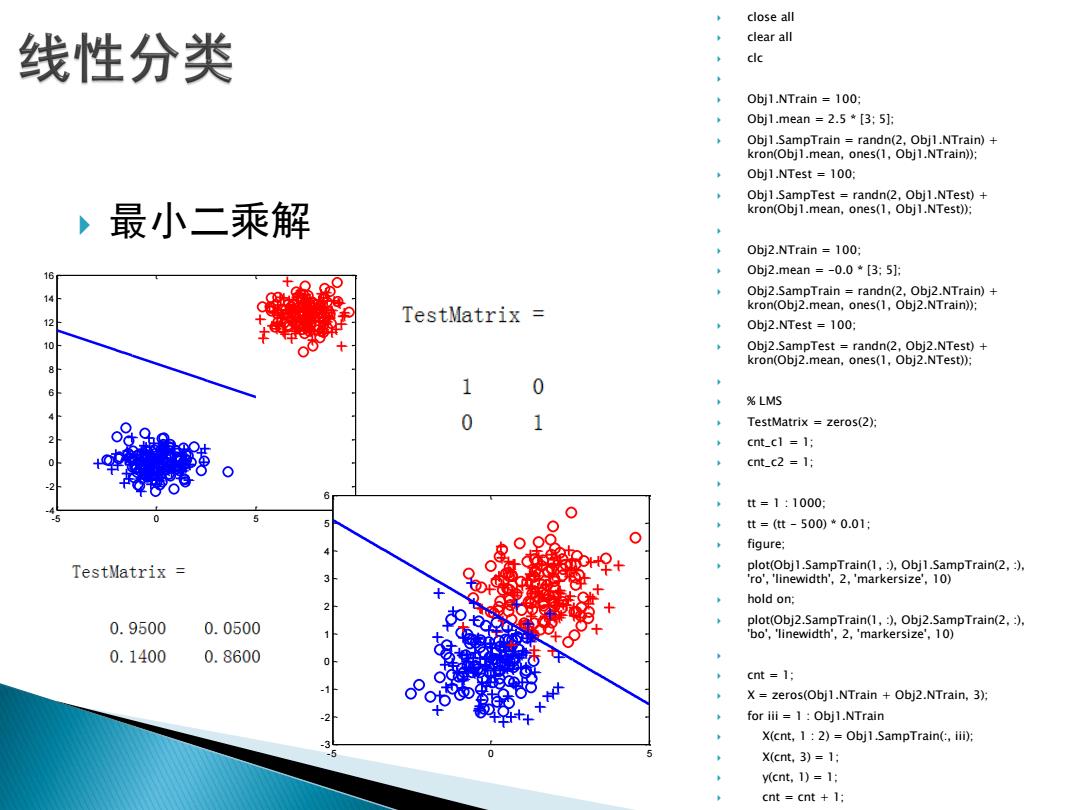
 最小二乘解  close all  clear all  clc  Obj1.NTrain = 100;  Obj1.mean = 2.5 * [3; 5];  Obj1.SampTrain = randn(2, Obj1.NTrain) + kron(Obj1.mean, ones(1, Obj1.NTrain));  Obj1.NTest = 100;  Obj1.SampTest = randn(2, Obj1.NTest) + kron(Obj1.mean, ones(1, Obj1.NTest));  Obj2.NTrain = 100;  Obj2.mean = -0.0 * [3; 5];  Obj2.SampTrain = randn(2, Obj2.NTrain) + kron(Obj2.mean, ones(1, Obj2.NTrain));  Obj2.NTest = 100;  Obj2.SampTest = randn(2, Obj2.NTest) + kron(Obj2.mean, ones(1, Obj2.NTest));  % LMS  TestMatrix = zeros(2);  cnt_c1 = 1;  cnt_c2 = 1;  tt = 1 : 1000;  tt = (tt - 500) * 0.01;  figure;  plot(Obj1.SampTrain(1, :), Obj1.SampTrain(2, :), 'ro', 'linewidth', 2, 'markersize', 10)  hold on;  plot(Obj2.SampTrain(1, :), Obj2.SampTrain(2, :), 'bo', 'linewidth', 2, 'markersize', 10)  cnt = 1;  X = zeros(Obj1.NTrain + Obj2.NTrain, 3);  for iii = 1 : Obj1.NTrain  X(cnt, 1 : 2) = Obj1.SampTrain(:, iii);  X(cnt, 3) = 1;  y(cnt, 1) = 1;  cnt = cnt + 1; end - 5 0 5 10 - 4 - 202468 10 12 14 16 - 5 0 5 - 3 - 2 - 10123456

线性分类 ,均方误差准则 给定样本x∈O,其希望标签为“1”，线性分类器输出为，=wX, 误差为：e=1-y,=1-wx=1-xw 给定o,类样本的似然函数为：p(x/o)以及®的先验概率：P(@) 则，o类样本误差为： J(@iw)=P(@,)(I-x"w)p(x/@)dx 总均方误差为： J(w)=J(0;w)+J(0;w) =P(@)[(I-x'w)"p(x/@)dx+P(@2)(1+x"w)"p(x/@2)dx

 均方误差准则 1 1 1 1 1 2 1 1 1 1 1 1 1 , = , ˆ 1 1 1 ˆ ( / ) ( ) ( ) ( ) (1 ) ( / ) ( ) ( ) ( ) = ( ) (1 ) T i i T T i i i T T y e y p P J P p d J J J P                         x w x w x x w x w x w x x w w w x w “” = ， ; ; ; 给定样本 线性分类器输出为 误差为: 给定 类样本的似然函数为： 则 总均方误差为： 1 , 其希望标签为 以及ω 的先验概率： 类样本误差为： 2 2 1 2 2 ( / ) ( ) (1 ) ( / ) T p d P p d        x x x w x x

线性分类 ,最小均方误差 a/(w) OP(@)(1-x"w)p(x/@)dx Ow Ow OP(@2)(1+x"w)p(x/@2)dx Ow -P(@,)[(-2x"+xx"w)p(x/@.)dx +P(@2)[(2x"+xx"w)p(x/@2)dx →E[xx]w=E[y→we=(E[x])E[y

 最小均方误差           2 1 1 2 2 2 1 1 2 2 1 ( ) (1 ) ( / ) ( ) ( ) (1 ) ( / ) ( ) 2 ( / ) ( ) 2 ( / ) T T T T T T T T MSE P p d J P p d P p d P p d y y                                         w x w x x w w x w x x w x xx w x x x xx w x x E xx w E x w E xx E x