
Bandit Convex Optimization(BCO) BCO with one-point feedback the learner sends a single point wt Ew,and then receives the function value fi(wt)only ry Amazon Prime e today and get unlimited fast,FREE shipping [Flaxman et al.,SODA 2005;Bubeck et al,STOC 2017] spired by you pping trends BCO with two-point feedback the learner sends two points wi,w?W, and then receives their function values,namely, fi(w)and fi(w?),only online recommendation [Agarwal et al.,COLT 2010;Shamir,JMLR 2017] Peng Zhao (Nanjing University) 16
Peng Zhao (Nanjing University) 16 Bandit Convex Optimization (BCO) • BCO with one-point feedback [Flaxman et al., SODA 2005; Bubeck et al., STOC 2017] • BCO with two-point feedback [Agarwal et al., COLT 2010; Shamir, JMLR 2017] online recommendation
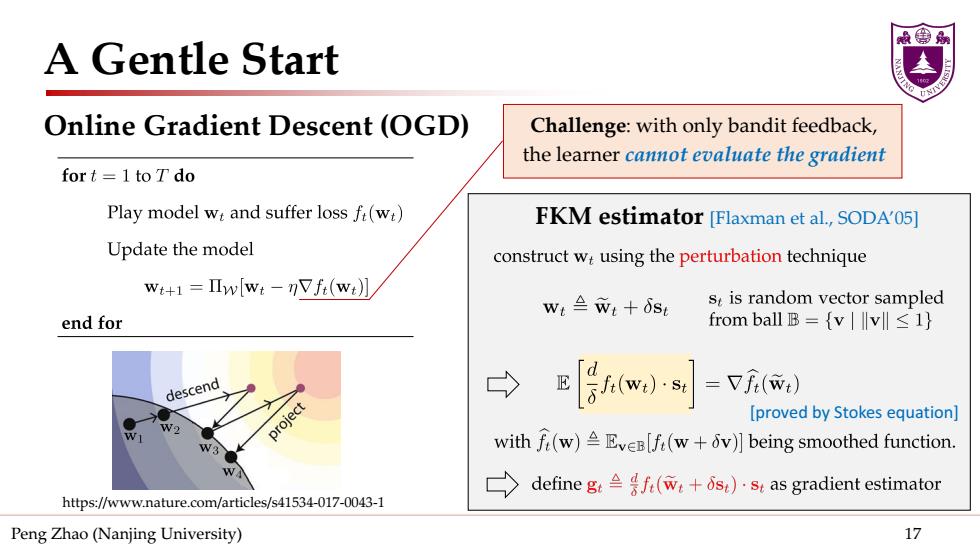
A Gentle Start Online Gradient Descent(OGD) Challenge:with only bandit feedback, the learner cannot evaluate the gradient fort=1 to Tdo Play model w and suffer loss f(w) FKM estimator [Flaxman et al.,SODA'05] Update the model construct w:using the perturbation technique wt+1=Πw[wt-Vf(wt】 wL≌wt+δst st is random vector sampled end for from ball B={vv1} descend =Vf() project [proved by Stokes equation] with f(w)Eve[f(w+v)]being smoothed function. define gf(w+s).s as gradient estimator https://www.nature.com/articles/s41534-017-0043-1 Peng Zhao (Nanjing University) 17
Peng Zhao (Nanjing University) 17 A Gentle Start Online Gradient Descent (OGD) https://www.nature.com/articles/s41534-017-0043-1 FKM estimator [Flaxman et al., SODA’05] Challenge: with only bandit feedback, the learner cannot evaluate the gradient [proved by Stokes equation]

A Gentle Start Online Gradient Descent(OGD) Challenge:with only bandit feedback, the learner cannot evaluate the gradient fort=1 to T do Play model wt and suffer loss fi(wt) FKM estimator [Flaxman et al.,SODA05] Update the model construct w:using the perturbation technique wt+1=Πw[wt-nVf(w)刃 w:≌wt+6st st is random vector sampled end for from ball B={vv1} Consider the 1-dim case(d=1). descend project [8w+网 2苏f(峦+d) 2苏(m-) https://www.nature.com/articles/s41534-017-0043-1 Peng Zhao (Nanjing University) 18
Peng Zhao (Nanjing University) 18 A Gentle Start Online Gradient Descent (OGD) https://www.nature.com/articles/s41534-017-0043-1 Challenge: with only bandit feedback, the learner cannot evaluate the gradient Consider the 1-dim case (𝒅𝒅 = 𝟏𝟏). FKM estimator [Flaxman et al., SODA’05]

Base Algorithm BGD ●Gradient estimator::gt=号ft(wt+st)·st Perform Online Gradient Descent using this gradient estimator. Bandit Gradient Descent(BGD) fort=1 to T do Select a unit vector st uniformly at random Submit wt=wt+st Receive ft(wt)as the feedback Construct the gradient estimator by g=f(w:+6s).st E[gi]=Vf(wt) wt+1=Πa-a)wlwt-门g] end for f(w)≌EveB[f:(w+v)】 Peng Zhao(Nanjing University) 19
Peng Zhao (Nanjing University) 19 Bandit Gradient Descent (BGD) Base Algorithm : BGD

Base Algorithm:Dynamic Regret Theorem 1.Under certain standard assumptions,for any perturbation parameter 6>0,step size n>0,and shrinkage parameter a =6/r,the expected dynamic regret of BGD(T,6,a,n)for the one-point feedback model satisfies 4切 202 where Pr=u measures the non-stationarity level. Optimal parameter setting is step size n=( →O(T3/4(1+P)1/4) perturbation parameter .=n Peng Zhao(Nanjing University) 20
Peng Zhao (Nanjing University) 20 Base Algorithm: Dynamic Regret Optimal parameter setting is